All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 8 Lesson 6 Compare and Order Fractions will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Answer Key Chapter 8 Lesson 6 Compare and Order Fractions
To compare fractions, create equivalent fractions with the same denominators or the same numerators. Use the least common multiple, or the least multiple common to sets of multiples.
Math in My World
Example 1
Ramon has an insect collection. The table shows the lengths of four insects in his collection. Which is longer, a mosquito or a whirligig beetle?

1. Find the least common multiple of the denominators.

The least common multiple of the denominators is ________________.
2. Create equivalent fractions that use 8 as the denominator.

3. Compare the numerators.
When the denominators are the same, the fraction with the greater numerator is the greater fraction.
\(\frac{2}{8}\) < \(\frac{3}{8}\) ← Of the numbers 2 and 3, 3 is closer to 8. So, 2 out of 8 is smaller than 3 out of 8.
So, a _____________ is longer.
Answer:
A Whirligig Bettle \(\frac{3}{8}\) is longer than Mosquito \(\frac{1}{4}\)
Explanation:
Mosquito = \(\frac{1}{4}\)
Whirligig Bettle = \(\frac{3}{8}\)
Multiplies of the denominators:
Multiplies of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40.
Multiplies of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80.
The least common multiple of the denominators 4 and 8 = 8.
Equivalent fractions that use 8 as the denominator:
\(\frac{1}{4}\) = \(\frac{1}{4}\) × \(\frac{2}{2}\) = \(\frac{2}{8}\)
\(\frac{3}{8}\) = \(\frac{3}{8}\) × \(\frac{1}{1}\) = \(\frac{3}{8}\)
Compare the numerators:
When the denominators are the same, the fraction with the greater numerator is the greater fraction.
\(\frac{2}{8}\) < \(\frac{3}{8}\) ← Of the numbers 2 and 3, 3 is closer to 8. So, 2 out of 8 is smaller than 3 out of 8.
So, a Whirligig Bettle is longer.
Example 2
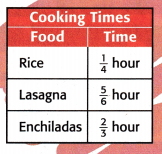
The table shows the cooking times needed for different foods. Order the foods from least to greatest cooking times.
1. Find the least common multiple of the numerators.
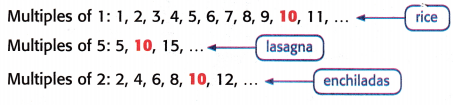
The least common multiple of the numerators is ________________.
2. Generate equivalent fractions that use 10 as the numerator.
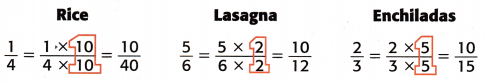
3. Compare the denominators.
When the numerators are the same, the fraction with the greatest denominator is the least fraction.
\(\frac{10}{40}\) < \(\frac{10}{15}\) < \(\frac{10}{12}\) ← Ib is much closer to 12 than it is to 40, so 10 out of 40 is smaller than lo out of 12.
So, from least to greatest cooking times, the foods are ______________, ______________ and ______________.
Check:
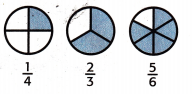
The models show \(\frac{1}{4}\) < \(\frac{2}{3}\) < \(\frac{5}{6}\).
Answer:
So, from least to greatest cooking times, the foods are Rice, Lasagna and Enchiladas.
The models show \(\frac{1}{4}\) < \(\frac{2}{3}\) < \(\frac{5}{6}\).
Explanation:
Rice = \(\frac{1}{4}\)
Lasagna = \(\frac{2}{3}\)
Enchiladas = \(\frac{5}{6}\).
Multiplies of the denominators:
Multiplies of 1: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
Multiplies of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20.
Multiplies of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50.
Least common multiple of the numerators 1, 2, 5 = 10.
Equivalent fractions:
\(\frac{1}{4}\) = \(\frac{1}{4}\) × \(\frac{10}{10}\) = \(\frac{10}{40}\)
\(\frac{2}{3}\) = \(\frac{2}{3}\) × \(\frac{5}{5}\) = \(\frac{10}{15}\)
\(\frac{5}{6}\) = \(\frac{5}{6}\) × \(\frac{2}{2}\) = \(\frac{10}{12}\)
Compare the denominators:
When the numerators are the same, the fraction with the greatest denominator is the least fraction.
\(\frac{10}{40}\) < \(\frac{10}{15}\) < \(\frac{10}{12}\)
Rice < Lasagna < Enchiladas

Talk Math
Explain how to compare \(\frac{7}{12}\) and \(\frac{2}{6}\).

Answer:
\(\frac{7}{12}\) is greater than \(\frac{2}{6}\).
Explanation:
\(\frac{7}{12}\) = 0.583.
\(\frac{2}{6}\) = \(\frac{2}{6}\) ÷ \(\frac{2}{2}\) = \(\frac{1}{3}\) = 0.333.
\(\frac{7}{12}\) > \(\frac{2}{6}\).
Guided Practice
Compare. Use >, <, or =.
Question 1.
\(\frac{3}{4}\) ![]() \(\frac{1}{2}\)
\(\frac{1}{2}\)
Answer:
\(\frac{3}{4}\) is greater than \(\frac{1}{2}\)
Explanation:
\(\frac{3}{4}\) = 0.75
\(\frac{1}{2}\) = 0.50.
\(\frac{3}{4}\) > \(\frac{1}{2}\)
Question 2.
\(\frac{3}{6}\) ![]() \(\frac{3}{4}\)
\(\frac{3}{4}\)
Answer:
\(\frac{3}{6}\) is lesser than \(\frac{3}{4}\)
Explanation:
\(\frac{3}{6}\) = \(\frac{3}{6}\) ÷ \(\frac{3}{3}\) = \(\frac{1}{2}\) = 0.50.
\(\frac{3}{4}\) = 0.75.
\(\frac{3}{6}\) < \(\frac{3}{4}\)