All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 8 Lesson 3 Model Equivalent Fractions will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Answer Key Chapter 8 Lesson 3 Model Equivalent Fractions
The top number on a fraction is the numerator, The bottom number on a fraction is the denominator. Fractions that represent the same part of a number are equivalent fractions.
Build it
Generate two fractions that are equivalent to \(\frac{1}{3}\).
1. Model \(\frac{1}{3}\).
Place a \(\frac{1}{3}\) – tile.
2. Find a fraction equivalent to \(\frac{1}{3}\).
Place \(\frac{1}{6}\) – tiles below the \(\frac{1}{3}\) – tile to equal the length of the \(\frac{1}{3}\) – tile.
How many \(\frac{1}{6}\) – tiles did you place?
So, \(\frac{1}{3}\) and \(\frac{2}{6}\) are equivalent fractions.
3. Find another fraction equivalent to \(\frac{1}{3}\).
Place \(\frac{1}{12}\) – tiles below the \(\frac{1}{6}\) – tiles to equal the length of the \(\frac{1}{3}\) – tile.
How many \(\frac{1}{12}\) – tiles did you place?
So, \(\frac{1}{3}\) and \(\frac{4}{12}\) are equivalent fractions.
So, \(\frac{1}{3}\),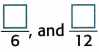 
are equivalent fractions.
Answer:
Equivalent fractions of \(\frac{1}{3}\) = \(\frac{4}{12}\) and \(\frac{2}{6}\).
Explanation:
Fraction given: \(\frac{1}{3}\)
\(\frac{1}{3}\) = \(\frac{1}{3}\) × \(\frac{4}{4}\) = \(\frac{4}{12}\).
\(\frac{1}{3}\) = \(\frac{1}{3}\) × \(\frac{2}{2}\) = \(\frac{2}{6}\)
Try It
Generate two fractions that are equivalent to \(\frac{1}{4}\).
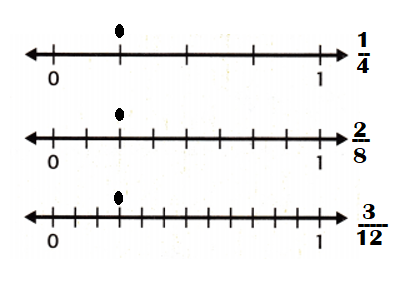
1. The first number line is divided into fourths. Plot \(\frac{1}{4}\) on the number line.
2. The second number line is divided into eighths.
What fraction is at the same location as \(\frac{1}{4}\)? 
Plot this fraction on the number line.
3. The third number line is divided into twelfths.
What fraction is at the same location as \(\frac{1}{4}\)?
Plot this fraction on the number line.
So, two fractions that are equivalent to \(\frac{1}{4}\) are and .
Answer:
Explanation:
Equivalent fraction:
\(\frac{1}{4}\) = \(\frac{1}{4}\) × \(\frac{2}{2}\) = \(\frac{2}{8}\)
\(\frac{1}{4}\) = \(\frac{1}{4}\) × \(\frac{3}{3}\) = \(\frac{3}{12}\)
Talk About It
Question 1.
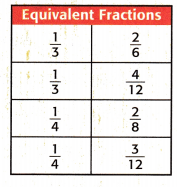
Mathematical PRACTICE Look for a Pattern The table shows some equivalent fractions. Study the table. Describe the pattern, between the numerators and denominators of two equivalent fractions.
Answer:
The denominators are different and numerators are same in the both fractions \(\frac{2}{6}\) and \(\frac{2}{8}\).
The numerators are different and denominators are same in the both fractions \(\frac{4}{12}\) and \(\frac{3}{12}\)
Explanation:
Equivalent fractions: \(\frac{1}{3}\) = \(\frac{2}{6}\) and \(\frac{4}{12}\)
Equivalent fractions: \(\frac{1}{4}\) = \(\frac{2}{8}\) and \(\frac{3}{12}\)
Question 2.
Mathematical PRACTICE Draw a Conclusion, determine whether \(\frac{1}{2}\) and \(\frac{3}{6}\) are equivalent fractions. Explain.
Answer:
Both fractions \(\frac{1}{2}\) and \(\frac{3}{6}\) are equivalent fractions.
Explanation:
\(\frac{1}{2}\) = \(\frac{1}{2}\)
\(\frac{3}{6}\) = \(\frac{3}{6}\) ÷ \(\frac{3}{3}\) = \(\frac{1}{2}\)
Practice It
Recognize whether the fractions are equivalent. Write yes or no.
Question 3.
\(\frac{2}{4}\) and \(\frac{6}{12}\)
Answer:
Yes, \(\frac{2}{4}\) and \(\frac{6}{12}\) both are equivalent fractions.
Explanation:
\(\frac{2}{4}\) = \(\frac{2}{4}\) ÷ \(\frac{2}{2}\) = \(\frac{1}{2}\)
\(\frac{6}{12}\) = \(\frac{6{12}\) ÷ \(\frac{6}{6}\) = \(\frac{1}{2}\)
Question 4.
\(\frac{6}{8}\) and \(\frac{5}{10}\)
Answer:
No, \(\frac{6}{8}\) and \(\frac{5}{10}\) both are not equivalent fractions.
Explanation:
\(\frac{6}{8}\) = \(\frac{6}{8}\) ÷ \(\frac{2}{2}\) = \(\frac{3}{4}\)
\(\frac{5}{10}\) = \(\frac{5}{10}\) ÷ \(\frac{5}{5}\) = \(\frac{1}{2}\)
Question 5.
\(\frac{2}{3}\) and \(\frac{3}{5}\)
Answer:
No, \(\frac{2}{3}\) and \(\frac{3}{5}\) both are not equivalent fractions.
Explanation:
\(\frac{2}{3}\) = \(\frac{2}{3}\)
\(\frac{3}{5}\) = \(\frac{2}{3}\)
Question 6.
\(\frac{9}{12}\) and \(\frac{3}{4}\)
Answer:
Yes, \(\frac{9}{12}\) and \(\frac{3}{4}\) both are equivalent fractions.
Explanation:
\(\frac{9}{12}\) = \(\frac{9}{12}\) ÷ \(\frac{3}{3}\) = \(\frac{3}{4}\)
\(\frac{3}{4}\) = \(\frac{3}{4}\)
Question 7.
\(\frac{4}{6}\) and \(\frac{8}{12}\)
Answer:
Yes, \(\frac{4}{6}\) and \(\frac{8}{12}\) both are equivalent fractions.
Explanation:
\(\frac{4}{6}\) = \(\frac{4}{6}\) ÷ \(\frac{2}{2}\) = \(\frac{2}{3}\)
\(\frac{8}{12}\) = \(\frac{8}{12}\) ÷ \(\frac{4}{4}\) = \(\frac{2}{3}\)
Question 8.
\(\frac{2}{3}\) and \(\frac{6}{10}\)
Answer:
No, \(\frac{2}{3}\) and \(\frac{6}{10}\) both are equivalent fractions.
Explanation:
\(\frac{2}{3}\) = \(\frac{2}{3}\)
\(\frac{6}{10}\) = \(\frac{6}{10}\) ÷ \(\frac{2}{2}\) = \(\frac{3}{5}\)
Generate two equivalent fractions for each fraction.
Question 9.
\(\frac{2}{4}\)
Answer:
Two equivalent fractions of \(\frac{2}{4}\) are \(\frac{4}{8}\) and \(\frac{12}{24}\)
Explanation:
\(\frac{2}{4}\) = \(\frac{2}{4}\) × \(\frac{2}{2}\) = \(\frac{4}{8}\)
\(\frac{2}{4}\) = \(\frac{2}{4}\) × \(\frac{6}{6}\) = \(\frac{12}{24}\)
Question 10.
\(\frac{2}{6}\)
Answer:
Two equivalent fractions of \(\frac{2}{6}\) are \(\frac{4}{12}\) and \(\frac{12}{36}\)
Explanation:
\(\frac{2}{6}\) = \(\frac{2}{6}\)× \(\frac{2}{2}\) = \(\frac{4}{12}\)
\(\frac{2}{6}\) = \(\frac{2}{6}\) × \(\frac{6}{6}\) = \(\frac{12}{36}\)
Question 11.
\(\frac{4}{8}\)
Answer:
Two equivalent fractions of \(\frac{4}{8}\) are \(\frac{16}{32}\) and \(\frac{32}{64}\)
Explanation:
\(\frac{4}{8}\) = \(\frac{4}{8}\) × \(\frac{4}{4}\) = \(\frac{16}{32}\)
\(\frac{4}{8}\) = \(\frac{4}{8}\)× \(\frac{8}{8}\) = \(\frac{32}{64}\)
Question 12.
\(\frac{5}{10}\)
Answer:
Two equivalent fractions of \(\frac{5}{10}\) are \(\frac{10}{20}\) and \(\frac{55}{110}\)
Explanation:
\(\frac{5}{10}\) = \(\frac{5}{10}\) × \(\frac{2}{2}\) = \(\frac{10}{20}\)
\(\frac{5}{10}\) = \(\frac{5}{10}\) × \(\frac{11}{11}\) = \(\frac{55}{110}\)
Question 13.
\(\frac{1}{3}\)
Answer:
Two equivalent fractions of \(\frac{1}{3}\) are \(\frac{5}{15}\) and \(\frac{3}{9}\)
Explanation:
\(\frac{1}{3}\) = \(\frac{1}{3}\)× \(\frac{5}{5}\) = \(\frac{5}{15}\)
\(\frac{1}{3}\) = \(\frac{1}{3}\)× \(\frac{3}{3}\) = \(\frac{3}{9}\)
Question 14.
\(\frac{2}{3}\)
Answer:
Two equivalent fractions of \(\frac{2}{3}\) are \(\frac{14}{21}\) and \(\frac{12}{18}\)
Explanation:
\(\frac{2}{3}\) = \(\frac{2}{3}\) × \(\frac{7}{7}\) = \(\frac{14}{21}\)
\(\frac{2}{3}\) = \(\frac{2}{3}\) × \(\frac{6}{6}\) = \(\frac{12}{18}\)
Apply It
Question 15.
Mathematical PRACTICE Model Math There were 10 baked goods in a basket. Four of them were sold. Write a fraction to show the part of the baked goods that were not sold. Then write an equivalent fraction to this number.
Answer:
Fraction to show the part of the baked goods that were not sold = \(\frac{2}{5}\)
Explanation:
Number of baked goods in a basket = 10.
Number of baked goods in a basket sold = 4.
Fraction to show the part of the baked goods that were not sold = Number of baked goods in a basket sold ÷ Number of baked goods in a basket
= 4 ÷ 10
= 2 ÷ 5 or \(\frac{2}{5}\)
Question 16.
Two-thirds of a jar of peanut butter has been used. Write an equivalent fraction.
Answer:
Equivalent fraction of \(\frac{2}{3}\) = \(\frac{10}{15}\)
Explanation:
Two-thirds of a jar of peanut butter has been used.
=> \(\frac{2}{3}\) = \(\frac{2}{3}\) × \(\frac{5}{5}\) = \(\frac{10}{15}\)
Question 17.
A jar has marbles in it. Three-tenths of the marbles are red. Five-tenths of the marbles are blue. Two-tenths of the marbles are green. Which of these fractions is equivalent to four-eighths?
Answer:
Fractions is equivalent to four-eighths = Fraction of the marbles are blue = \(\frac{5}{10}\)
Explanation:
Fraction of the marbles are red = \(\frac{3}{10}\)
Fraction of the marbles are blue = \(\frac{5}{10}\)
Fraction of the marbles are green = \(\frac{2}{10}\)
Simplest form:
\(\frac{3}{10}\) = \(\frac{3}{10}\)
\(\frac{5}{10}\) = \(\frac{5}{10}\) ÷ \(\frac{5}{5}\) = \(\frac{1}{2}\)
\(\frac{2}{10}\) = \(\frac{2}{10}\) ÷ \(\frac{2}{2}\) = \(\frac{1}{5}\)
\(\frac{4}{8}\) = \(\frac{4}{8}\) ÷ \(\frac{4}{4}\) = \(\frac{1}{2}\)
Question 18.
Mathematical PRACTICE Use Number Sense Daria used fraction tiles to show that \(\frac{3}{5}\) is equivalent to \(\frac{6}{10}\). Compare the number and size of fraction tiles needed to model each fraction.
Answer:
\(\frac{3}{5}\) is equivalent to \(\frac{6}{10}\) both are size are same.
Explanation:
Given: \(\frac{3}{5}\) is equivalent to \(\frac{6}{10}\).
\(\frac{3}{5}\)
\(\frac{6}{10}\) = \(\frac{6}{10}\) ÷ \(\frac{2}{2}\) = \(\frac{3}{5}\)
Question 19.
Mathematical PRACTICE Make Sense of Problems
Complete the equation.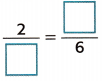 
Answer:
Equation: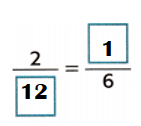 
Explanation:
Equation:
\(\frac{2}{??}\) × \(\frac{3}{3}\) = \(\frac{??}{6}\)
=> 6 × 2 = 12.
\(\frac{2}{12}\) = \(\frac{1}{6}\)
Write About It
Question 20.
Write a real-world example of equivalent fractions.
Answer:
A real-world example of equivalent fractions is a piece of cake.
Explanation:
I have a cake, cut it into two equal pieces, and eat one of them, you will have eaten half the cake. If I cut a cake into eight equal pieces and eat four of them, I will still have eaten half the cake. These are equivalent fractions.
McGraw Hill My Math Grade 4 Chapter 8 Lesson 3 My Homework Answer Key
Practice
Recognize whether the fractions are equivalent. Write yes or no.
Question 1.
\(\frac{3}{5}\) and \(\frac{6}{8}\)
Answer:
Yes, \(\frac{3}{5}\) and \(\frac{6}{8}\) both are equivalent fractions.
Explanation:
\(\frac{3}{5}\) = \(\frac{3}{5}\)
\(\frac{6}{8}\) = \(\frac{6}{8}\) ÷ \(\frac{2}{2}\) = \(\frac{3}{5}\)
Question 2.
\(\frac{4}{5}\) and \(\frac{5}{6}\)
Answer:
No \(\frac{4}{5}\) and \(\frac{5}{6}\) both are not equivalent fractions.
Explanation:
\(\frac{4}{5}\) = \(\frac{4}{5}\)
\(\frac{5}{6}\) = \(\frac{5}{6}\)
Question 3.
\(\frac{2}{4}\) and \(\frac{6}{12}\)
Answer:
Yes \(\frac{2}{4}\) and \(\frac{6}{12}\) both are equivalent fractions.
Explanation:
\(\frac{2}{4}\) = \(\frac{2}{4}\) ÷ \(\frac{2}{2}\) = \(\frac{1}{2}\)
\(\frac{6}{12}\) = \(\frac{6}{12}\) ÷ \(\frac{6}{6}\) = \(\frac{1}{2}\)
Question 4.
\(\frac{2}{3}\) and \(\frac{4}{6}\)
Answer:
Yes \(\frac{2}{3}\) and \(\frac{4}{6}\) both are equivalent fractions.
Explanation:
\(\frac{2}{3}\) = \(\frac{2}{3}\)
\(\frac{4}{6}\) = \(\frac{4}{6}\) ÷ \(\frac{2}{2}\) = \(\frac{2}{3}\)
Question 5.
\(\frac{8}{12}\) and \(\frac{4}{6}\)
Answer:
Yes \(\frac{8}{12}\) and \(\frac{4}{6}\) both are equivalent fractions.
Explanation:
\(\frac{8}{12}\) = \(\frac{8}{12}\) ÷ \(\frac{4}{4}\) = \(\frac{2}{3}\)
\(\frac{4}{6}\) = \(\frac{4}{6}\) ÷ \(\frac{2}{2}\) = \(\frac{2}{3}\)
Question 6.
\(\frac{5}{6}\) and \(\frac{9}{10}\)
Answer:
No \(\frac{5}{6}\) and \(\frac{9}{10}\) both are not equivalent fractions.
Explanation:
\(\frac{5}{6}\) = \(\frac{5}{6}\)
\(\frac{9}{10}\) = \(\frac{9}{10}\)
Generate two equivalent fractions for each fraction.
Question 7.
\(\frac{1}{3}\)
Answer:
Two equivalent fractions of \(\frac{1}{3}\) are \(\frac{7}{21}\) and \(\frac{3}{9}\)
Explanation:
\(\frac{1}{3}\) = \(\frac{1}{3}\) × \(\frac{7}{7}\) = \(\frac{7}{21}\)
\(\frac{1}{3}\) = \(\frac{1}{3}\) × \(\frac{3}{3}\) = \(\frac{3}{9}\)
Question 8.
\(\frac{8}{12}\)
Answer:
Two equivalent fractions of \(\frac{8}{12}\) are \(\frac{16}{24}\) and \(\frac{24}{36}\)
Explanation:
\(\frac{8}{12}\) = \(\frac{8}{12}\) × \(\frac{2}{2}\) = \(\frac{16}{24}\)
\(\frac{8}{12}\) = \(\frac{8}{12}\) × \(\frac{3}{3}\) = \(\frac{24}{36}\)
Question 9.
\(\frac{3}{4}\)
Answer:
Two equivalent fractions of \(\frac{3}{4}\) are \(\frac{15}{20}\) and \(\frac{6}{8}\)
Explanation:
\(\frac{3}{4}\) = \(\frac{3}{4}\) × \(\frac{5}{5}\) = \(\frac{15}{20}\)
\(\frac{3}{4}\) = \(\frac{3}{4}\) × \(\frac{2}{2}\) = \(\frac{6}{8}\)
Problem Solving
Question 10.
Mathematical PRACTICE Justify Conclusions Francie lives \(\frac{1}{5}\) mile from the school. Jake lives \(\frac{2}{10}\) mile from the school. Do they live the same distance from the school? Explain.
Answer:
Yes, they live the same distance from the school because \(\frac{1}{5}\) is the simplest form of \(\frac{2}{10}\).
Explanation:
Number of miles Francie lives from the school = \(\frac{1}{5}\)
Number of miles Jake lives from the school = \(\frac{2}{10}\)
Simplest form:
\(\frac{1}{5}\) = \(\frac{1}{5}\)
\(\frac{2}{10}\) = \(\frac{2}{10}\) ÷ \(\frac{2}{2}\) = \(\frac{1}{5}\)
Vocabulary Check
Draw a line to match the vocabulary term with its example.
Answer:
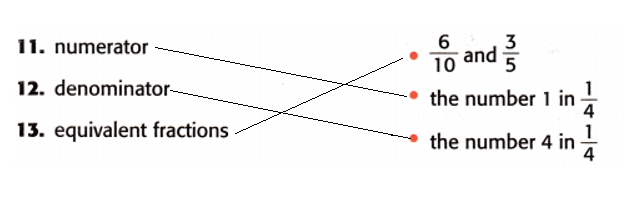
Explanation:
Numerator = the number above the line in a fraction showing how many of the parts indicated by the denominator are taken.
The denominator = The numeric value below the line of a fraction is called the denominator.
Equivalent fractions = They are fractions that represent the same value, even though they look different.