All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 8 Lesson 10 Mixed Numbers and Improper Fractions will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Answer Key Chapter 8 Lesson 10 Mixed Numbers and Improper Fractions
An improper fraction has a numerator that is greater than or equal to its denominator. Mixed numbers can be written as improper fractions.
Math in My World
Example 1
Nyoko is selling pies at a bake sale. Each pie has 5 slices. There are 7 slices left. What fraction of the pies is left?
One Way
Count the wholes and the parts.
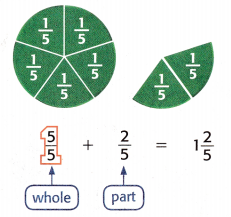
Another Way
Count the parts.
So,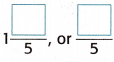 
, of the pies is left.
Answer:
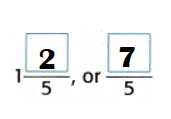
Fraction of the pies is left = \(\frac{7}{5}\) or 1\(\frac{2}{5}\)
Explanation:
Number of slices each pie has = 5.
Number of slices left = 7.
Fraction of the pies is left = Number of slices left ÷ Number of slices each pie has
= 7 ÷ 5 or \(\frac{7}{5}\) or 1\(\frac{2}{5}\)
You can change a mixed number to an improper fraction. You can also change an improper fraction to a mixed number.
Example 2
Write 1\(\frac{3}{8}\) as an improper fraction.
The model shows 1\(\frac{3}{8}\).
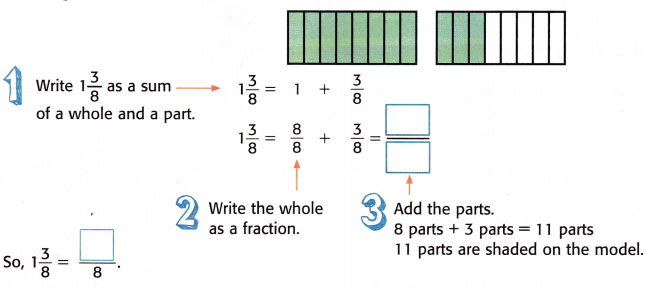
Answer:
Improper fraction of 1\(\frac{3}{8}[/latex = [latex]\frac{11}{8}\)
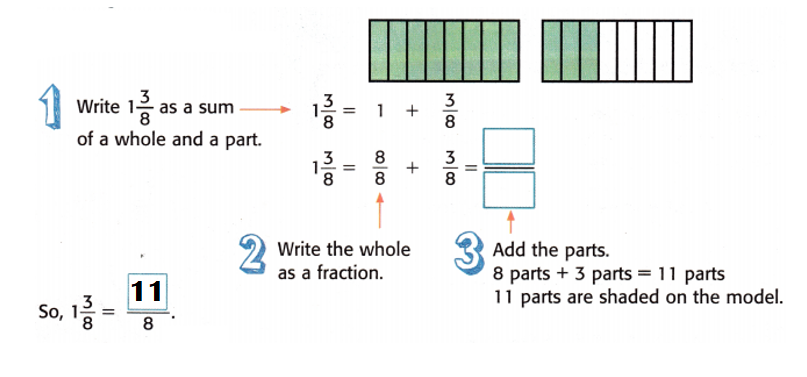
Explanation:
Mixed fraction:
1\(\frac{3}{8}[/latex = [(1 × 8) + 3] ÷ 8
= (8 + 3) ÷ 8
= 11 ÷ 8 or [latex]\frac{11}{8}\)
Example 3
Write \(\frac{9}{4}\) as a mixed number.
The model shows 9 divided into groups of 4.
There are 2 wholes and 1 out of 4 left over.
So, \(\frac{9}{4}\) =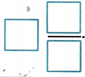 
.
Answer:
So, \(\frac{9}{4}\) =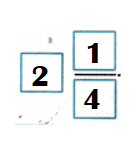 
Explanation:
\(\frac{9}{4}\)
There are 2 wholes and 1 out of 4 left over.
= 2\(\frac{1}{4}\)
Talk Math
Why does the improper fraction and mixed number for Exercise 1 have the same denominator?
Answer:
The improper fraction and mixed number for Exercise 1 have the same denominator because number of the whole parts are same.
Explanation:
Improper Fraction = A fraction whose numerator is larger than the denominator.
Mixed Number = An integer combined with a proper fraction showing how many wholes and how many parts are in the number.
Guided Practice
Question 1.
Write a mixed number and an improper fraction for the shaded model.
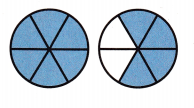
Answer:
Improper fraction = \(\frac{9}{4}\)
Mixed fraction of \(\frac{9}{4}\) = 2\(\frac{1}{4}\)
Explanation:
Number of shaded parts = 9.
Number of parts = 5.
Improper fraction = Number of shaded parts ÷ Number of parts
= 9 ÷ 5 or \(\frac{9}{5}\)
Mixed fraction = \(\frac{9}{4}\) = 2\(\frac{1}{4}\)
McGraw Hill My Math Grade 4 Chapter 8 Lesson 10 My Homework Answer Key
Practice
Write a mixed number and an improper fraction for each shaded model.
Question 1.
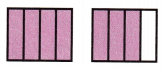
Answer:
Improper fraction = \(\frac{7}{4}\)
Mixed fraction of \(\frac{7}{4}\) = 1\(\frac{3}{4}\)
Explanation:
Number of shaded parts = 7.
Number of parts = 4.
Improper fraction = Number of shaded parts ÷ Number of parts
= 7 ÷ 4 or \(\frac{7}{4}\)
Mixed fraction = \(\frac{7}{4}\) = 1\(\frac{3}{4}\)
Question 2.
Answer:
Improper fraction = \(\frac{8}{3}\)
Mixed fraction of \(\frac{8}{3}\) = 2\(\frac{2}{3}\)
Explanation:
Number of shaded parts = 8.
Number of parts = 3.
Improper fraction = Number of shaded parts ÷ Number of parts
= 8 ÷ 3 or \(\frac{7}{3}\)
Mixed fraction = \(\frac{8}{3}\) = 2\(\frac{2}{3}\)
Write a mixed number and an improper fraction for each model.
Question 3.
Answer:
Improper fraction = \(\frac{13}{4}\)
Mixed fraction of \(\frac{13}{4}\) = 3\(\frac{1}{4}\)
Explanation:
Number of shaded parts = 13.
Number of parts = 4.
Improper fraction = Number of shaded parts ÷ Number of parts
= 13 ÷ 4 or \(\frac{13}{4}\)
Mixed fraction = \(\frac{13}{4}\) = 3\(\frac{1}{4}\)
Question 4.
Answer:
Improper fraction = \(\frac{17}{12}\)
Mixed fraction of \(\frac{17}{12}\) = 1\(\frac{5}{12}\)
Explanation:
Number of shaded parts = 17.
Number of parts = 12.
Improper fraction = Number of shaded parts ÷ Number of parts
= 17 ÷ 12 or \(\frac{17}{12}\)
Mixed fraction = \(\frac{17}{12}\)= 1\(\frac{5}{12}\)
Question 5.
Draw a model to write 2\(\frac{3}{5}\) as an improper fraction.
Answer:
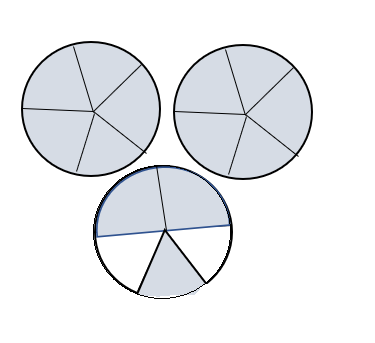
Explanation:
2\(\frac{3}{5}\) = [(2 × 5) + 3] ÷ 5
= (10 + 3) ÷ 5
= 13 ÷ 5 or \(\frac{13}{5}\)
Question 6.
Draw a model to write \(\frac{30}{4}\) as a mixed number.
Answer:
Mixed number of \(\frac{30}{4}\) = 7\(\frac{2}{4}\)
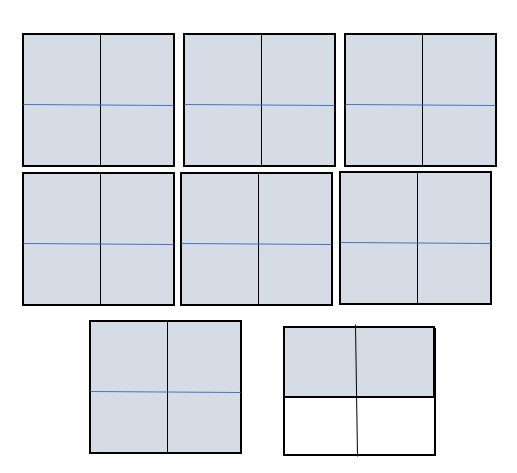
Explanation:
\(\frac{30}{4}\) = 7 × 4 = 28 + 2 = 30.
= 7\(\frac{2}{4}\)
Problem Solving
Question 7.
Mathematical PRACTICE Use Number Sense Ana walked \(\frac{13}{3}\) miles. Write \(\frac{13}{3}\) as a mixed number.
Answer:
Mixed number of \(\frac{13}{3}\) = 4\(\frac{1}{3}\)
Explanation:
Number of miles of Ana walked = \(\frac{13}{3}\)
Mixed number:
\(\frac{13}{3}\) = 4\(\frac{1}{3}\)
Question 8.
There are 5\(\frac{4}{5}\) cups of milk left in a carton. Write 5\(\frac{4}{5}\) as an improper fraction.
Answer:
Improper fraction of 5\(\frac{4}{5}\) = \(\frac{29}{5}\)
Explanation:
Number of cups of milk left in a carton = 5\(\frac{4}{5}\)
Improper fraction:
5\(\frac{4}{5}\) = [(5 × 5) + 4] ÷ 5
= (25 + 4) ÷ 5
= 29 ÷ 5 or \(\frac{29}{5}\)
Vocabulary Check
Question 9.
Is \(\frac{10}{3}\) an improper fraction? Explain.
Answer:
\(\frac{10}{3}\) is an improper fraction because the numerator is greater than the denominator.
Explanation:
An improper fraction is a fraction where the numerator is greater than or equal to the denominator.
\(\frac{10}{3}\)
Test Practice
Question 10.
Amelia needs 3\(\frac{2}{3}\) cups of sugar to make cupcakes. Which improper fraction names this amount?
(A) \(\frac{5}{3}\) cups
(B) \(\frac{8}{3}\) cups
(C) \(\frac{11}{3}\) cups
(D) \(\frac{18}{3}\) cups
Answer:
Improper fraction names this amount = \(\frac{2}{3}\) cups.
(C) \(\frac{11}{3}\) cups
Explanation:
Number of cups of sugar Amelia needs to make cupcakes = 3\(\frac{2}{3}\).
Improper fraction:
3\(\frac{2}{3}\) = [(3 × 3) + 2] ÷ 3
= (9 + 2) ÷ 3
= 11 ÷ 3 or \(\frac{2}{3}\) cups.