All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 8 Check My Progress will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Chapter 8 Check My Progress Answer Key
Check My Progress Page No. (529 – 530)
Vocabulary Check
Question 1.
Write two equivalent fractions.
Answer:
Two equivalent fractions are \(\frac{1}{2}\) and \(\frac{5}{10}\).
Explanation:
Equivalent fractions are the fractions that have different numerators and denominators but are equal to the same value.
Two equivalent fractions:
\(\frac{1}{2}\) and \(\frac{5}{10}\)
Question 2.
Write the fraction that has a 4 in the numerator and a 6 in the denominator.
Answer:
The fraction that has a 4 in the numerator and a 6 in the denominator = \(\frac{14}{16}\)
Explanation:
A fraction is a part of a whole. In arithmetic, the number is expressed as a quotient, in which the numerator is divided by the denominator.
Example: \(\frac{5}{10}\)
Question 3.
Write the fraction from Exercise 2 in simplest form.
Answer:
Simplest form:
\(\frac{14}{16}\) = \(\frac{7}{8}\)
Explanation:
Fraction in Exercise 2:
\(\frac{14}{16}\)
Simplest form:
\(\frac{14}{16}\) ÷ \(\frac{2}{2}\)
= \(\frac{7}{8}\)
Question 4.
Explain the difference between a greatest common factor and a least common multiple.
Answer:
The difference between a greatest common factor and a least common multiple is that
the greatest common factor (GCF) is the largest number that is a factor of two or more numbers, and the least common multiple (LCM) is the smallest number that is a multiple of two or more numbers.
Explanation:
The Greatest Common Factor (also known as GCF) is the largest number that divides evenly into each number in a given set of numbers. The Least Common Multiple (also known as LCM) is the smallest positive multiple that is common to two or more numbers.
Concept Check
Recognize whether the fractions are equivalent. Write yes or no.
Question 5.
\(\frac{1}{4}\) and \(\frac{3}{12}\)
Answer:
Yes, \(\frac{1}{4}\) and \(\frac{3}{12}\) both fractions are equivalent fractions.
Explanation:
Fractions given: \(\frac{1}{4}\) and \(\frac{3}{12}\)
\(\frac{1}{4}\) = \(\frac{1}{4}\)
\(\frac{3}{12}\) = \(\frac{3}{12}\) ÷ \(\frac{3}{3}\)
= \(\frac{1}{4}\)
Question 6.
\(\frac{4}{6}\) and \(\frac{6}{12}\)
Answer:
No, \(\frac{4}{6}\) and \(\frac{6}{12}\) both fractions are not equivalent fractions.
Explanation:
Fractions given: \(\frac{4}{6}\) and \(\frac{6}{12}\)
\(\frac{4}{6}\) = \(\frac{4}{6}\) ÷ \(\frac{2}{2}\)
= \(\frac{2}{3}\)
\(\frac{6}{12}\) = \(\frac{6}{12}\) ÷ \(\frac{2}{2}\)
= \(\frac{3}{6}\) ÷ \(\frac{3}{3}\)
= \(\frac{1}{2}\)
Question 7.
\(\frac{5}{10}\) and \(\frac{3}{6}\)
Answer:
Yes, \(\frac{5}{10}\) and \(\frac{3}{6}\) both fractions are equivalent fractions.
Explanation:
Fractions given: \(\frac{5}{10}\) and \(\frac{3}{6}\)
\(\frac{5}{10}\) = \(\frac{5}{10}\) ÷ \(\frac{5}{5}\)
= \(\frac{1}{2}\)
\(\frac{3}{6}\) = \(\frac{3}{6}\) ÷ \(\frac{3}{3}\)
= \(\frac{1}{2}\)
Generate two equivalent fractions for each fraction.
Question 8.
\(\frac{2}{8}\)
Answer:
Two equivalent fractions of \(\frac{2}{8}\) = \(\frac{6}{24\) and \(\frac{26}{104\)
Explanation:
Fraction given: \(\frac{2}{8}\)
Two equivalent fractions:
\(\frac{2}{8}\) × \(\frac{3}{3\) = \(\frac{6}{24\)
\(\frac{2}{8}\) × \(\frac{13}{13\) = \(\frac{26}{104\)
Question 9.
\(\frac{1}{3}\)
Answer:
Two equivalent fractions of \(\frac{1}{3}\) = \(\frac{4}{12\) and \(\frac{10}{30\)
Explanation:
Fraction given: \(\frac{1}{3}\)
Two equivalent fractions:
\(\frac{1}{3}\) × \(\frac{4}{4\) = \(\frac{4}{12\)
\(\frac{1}{3}\)× \(\frac{10}{10\) = \(\frac{10}{30\)
Question 10.
\(\frac{2}{4}\)
Answer:
Two equivalent fractions of \(\frac{2}{4}\) = \(\frac{12}{24\) and \(\frac{22}{44\)
Explanation:
Fraction given: \(\frac{2}{4}\)
Two equivalent fractions:
\(\frac{2}{4}\) × \(\frac{6}{6\) = \(\frac{12}{24\)
\(\frac{2}{4}\)× \(\frac{11}{11\) = \(\frac{22}{44\)
Problem Solving
Question 11.
Adina read 60 out of 100 pages in a comic book. Write the fraction of the pages she read in simplest form.
Answer:
Fraction of the pages she read in simplest form = \(\frac{3}{5}\)
Explanation:
Number of pages Adina read in a comic book = 60.
Total number of pages in a comic book = 100.
Fraction of the pages she read in simplest form = Number of pages Adina read in a comic book ÷ Total number of pages in a comic book
= 60 ÷ 100
= \(\frac{60}{100}\) ÷ \(\frac{10}{10}\)
= \(\frac{6}{10}\) ÷ \(\frac{2}{2}\)
= \(\frac{3}{5}\)
Question 12.
The table shows how much time each student needs to finish an art project. Does Simon need more or less time than Phil? Explain.
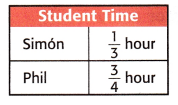
Answer:
Simon needs more time because Phil’s is almost to complete his to finish an art project.
Explanation:
Number of hours Simon takes = \(\frac{1}{3}\) [1 part completed in 3]
Number of hours Phil takes = \(\frac{3}{4}\) [3 part completed in 4]
Simon needs more time to to finish an art project.
Phil needs less time to to finish an art project.
Question 13.
Write the fraction for the part that is shaded. Then find an equivalent fraction.
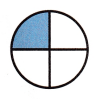
Answer:
The fraction for the part that is shaded = \(\frac{1}{4}\)
Equivalent fraction of \(\frac{1}{4}\) = \(\frac{5}{20}\)
Explanation:
Part that is shaded = 1.
Total number of parts = 4.
The fraction for the part that is shaded = Part that is shaded ÷ Total number of parts
= 1 ÷ 4 or \(\frac{1}{4}\)
Equivalent fraction:
\(\frac{1}{4}\) × \(\frac{5}{5}\) = \(\frac{5}{20}\)
Test Practice
Question 14.
Which fraction is in simplest form?
(A) \(\frac{2}{10}\)
(B) \(\frac{3}{12}\)
(C) \(\frac{4}{12}\)
(D) \(\frac{3}{8}\)
Answer:
\(\frac{3}{8}\) fraction is in simplest form.
(D) \(\frac{3}{8}\)
Explanation:
Fractions given:
(A) \(\frac{2}{10}\) = \(\frac{2}{10}\) ÷ \(\frac{2}{2}\)
= \(\frac{1}{5}\)
(B) \(\frac{3}{12}\) = \(\frac{3}{12}\) ÷ \(\frac{3}{3}\)
= \(\frac{1}{4}\)
(C) \(\frac{4}{12}\) = \(\frac{4}{12}\) ÷ \(\frac{4}{4}\)
= \(\frac{1}{3}\)
(D) \(\frac{3}{8}\) = \(\frac{3}{8}\)