All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 8 Fractions will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Answer Key Chapter 8 Fractions
Essential Question
How can different fractions name the same amount?
Answer:
When fractions have different numbers in them, but have the same value, they are called equivalent fractions.
Explanation:
When fractions have different numbers in them, but have the same value, they are called equivalent fractions.
They can be defined as fractions that may have different numerators and denominators but they represent the same value.
For example, 9/12 and 6/8 are equivalent fractions because both are equal to 3/4 when simplified
Am I Ready
Graph each fraction on a number line.
Question 1.
\(\frac{1}{3}\)

Answer:
\(\frac{1}{3}\) on number line =
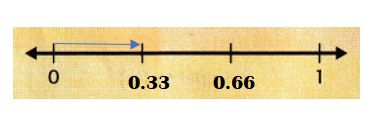
Explanation:
\(\frac{1}{3}\) = 0.33.
Question 2.
\(\frac{1}{6}\)

Answer:
\(\frac{1}{6}\) on number line =
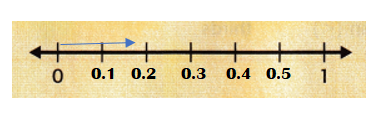
Explanation:
\(\frac{1}{6}\) = 0.166…
Question 3.
\(\frac{3}{8}\)

Answer:
\(\frac{3}{8}\) on number line =
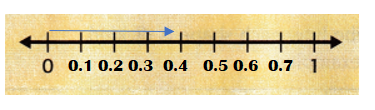
Explanation:
\(\frac{3}{8}\) = 0.375.
Use the number line to determine whether the two fractions are equivalent. Write yes or no.
Question 4.
\(\frac{1}{2}\) and \(\frac{4}{8}\)
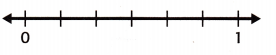
Answer:
\(\frac{1}{2}\) and \(\frac{4}{8}\) are both equivalent fractions.
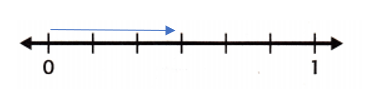
Explanation:
\(\frac{1}{2}\) = 0.5.
\(\frac{4}{8}\) = \(\frac{1}{2}\) = 0.5.
Question 5.
\(\frac{2}{3}\) and \(\frac{5}{6}\)
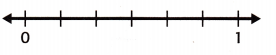
Answer:
\(\frac{2}{3}\) and \(\frac{5}{6}\) are both equivalent fractions.
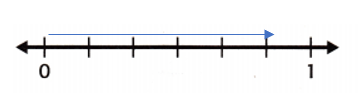
Explanation:
\(\frac{2}{3}\) = 0.666.
\(\frac{5}{6}\) = \(\frac{2}{3}\) = 0.666.
Write each whole number as a fraction.
Question 6.
5
Answer:
Fraction form of 5 = \(\frac{10}{2}\)
Explanation:
5 as fraction = \(\frac{10}{2}\)
\(\frac{10}{2}\) = \(\frac{5}{1}\) = 5.
Question 7.
9
Answer:
Fraction form of 9 = \(\frac{9}{1}\)
Explanation:
9 as fraction = \(\frac{9}{1}\)
My Math Words
Review Vocabulary
fourths
halves
is equal to (=)
is greater than (>)
is less than (<)
thirds
Making Connections
Use the review vocabulary to describe how each shape is divided. Then use symbols to compare the examples.
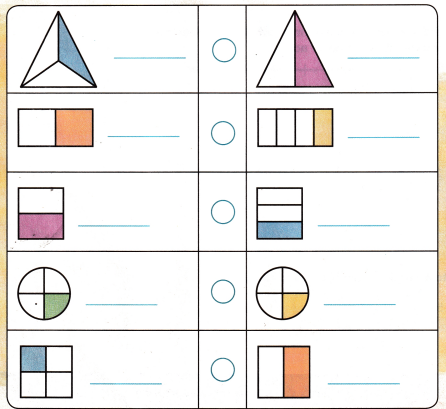
Answer:
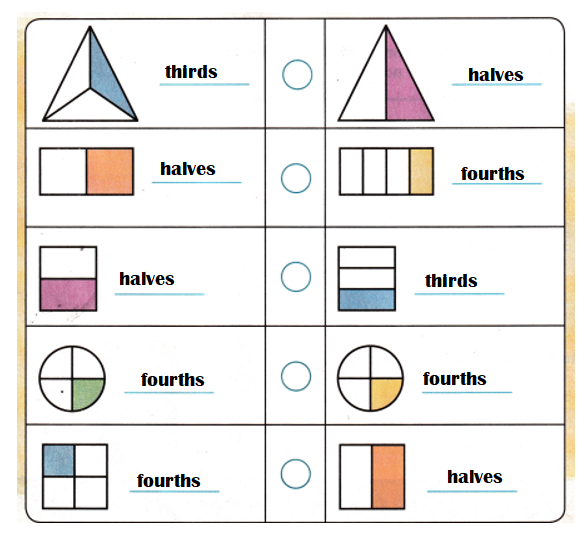
Explanation:
Review Vocabulary to be used in the table:
fourths = 1 part of four parts.
halves = half of any parts.
is equal to (=)
is greater than (>)
is less than (<)
thirds = one part of three parts.
My Vocabulary Cards
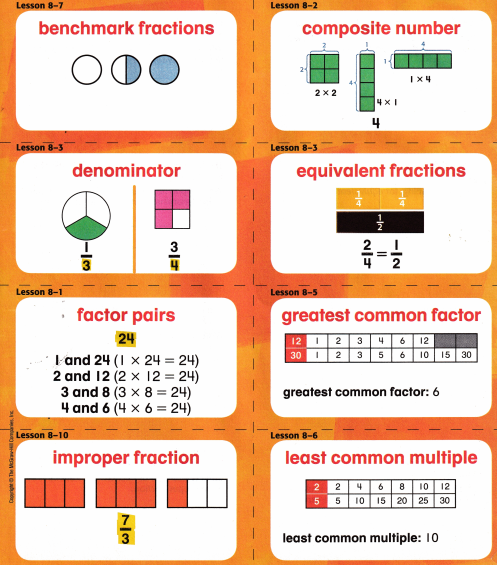
Ideas for Use
- Group 2 or 3 common words. Add a word that is unrelated to the group. Then work with a friend to name the unrelated word.
- Use a blank card to write this chapter’s essential question. Use the back of the card to write or draw examples that help you answer the question.
A whole number with more than two factors.
Describe what a composite number is based on the visuals shown on this card.
Answer:
Composite numbers are numbers with more than two factors. Numbers can be classified on the basis of the number of factors that they have is been shown on the visuals shown on this card.
Explanation:
A number that has more factors than itself and 1 is called a composite number because ‘1’ is neither prime nor composite , and its only factor is 1.
Composite numbers are numbers with more than two factors. Numbers can be classified on the basis of the number of factors that they have is been shown on the visuals shown on this card.
Common fractions that are used for estimation.
When do you see or use benchmark fractions in your everyday life?
Answer:
Benchmark fractions can be used in cooking or baking to tell how much of an ingredient to use in everyday life.
Explanation:
In math, benchmark fractions can be defined as common fractions that we can measure or judge against, when measuring, comparing, or ordering other fractions. Benchmark fractions are easy to visualize and identify, and thus, help in estimating the parts.
Fractions are used in baking to tell how much of an ingredient to use. Fractions are used in telling time; each minute is a fraction of the hour. Finally, fractions are used to determine discounts when there’s a sale going on.
Fractions that have the same value.
What is an antonym, or word with an opposite meaning, for equivalent?
Answer:
Some common synonyms of equivalent are equal, identical, same, selfsame, and very.
Some common opposites of equivalent are illogical physical nonintellectual integrate differentiate add divide.
Explanation:
Some common synonyms of equivalent are equal, identical, same, selfsame, and very. While all these words mean “not different or not differing from one another,” equivalent implies amounting to the same thing in worth or significance.
An antonym is a word that is the opposite of another word. An opposite can be the other side of, reverse of, or something contrary to anything, not just words. Some common opposites of equivalent are illogical physical nonintellectual integrate differentiate add divide.
The bottom number in a fraction. It tells the total number of equal parts.
Write a tip to help you remember which number is the denominator and which is the numerator.
Answer:
In the fraction \(\frac{1}{4}\) – 1 – Numerator , 4 – Denominator.
Explanation:
A fraction has two parts, namely numerator and denominator. The number on the top is called the numerator, and the number on the bottom is called the denominator.
As an example, the fraction \(\frac{1}{4}\) amounts to four parts, each of which is of the type named “fourth”.
1 – Numerator.
4 – Denominator.
The greatest of the common factors of each of two or more numbers.
The suffix -est is added to adjectives to mean the most.” Use another adjective with this suffix in a sentence.
Answer:
A suffix forming the superlative degree of adjectives and adverbs: warmest; fastest; soonest.
Example: She is the fastest runner among her friends.
Explanation:
A suffix is a type of affix. Suffixes change the meaning or grammatical function of a base word or root word. A suffix forming the superlative degree of adjectives and adverbs: warmest; fastest; soonest.
Example: She is the fastest runner among her friends.
The two factors that are multiplied to find a product.
Write 3 factor pairs of 36.
Answer:
3 Factor pairs of 36:
2 × 18 = 36.
3 × 12 = 36.
4 × 9 = 36.
Explanation:
Factor pairs of 36:
1 × 36 = 36.
2 × 18 = 36.
3 × 12 = 36.
4 × 9 = 36.
6 × 6 = 36.
The least multiple greater than 0 that is a common multiple of each of two or more numbers.
Write the 3 multiples that follow the multiples of 2 and 5 shown on the front of the card.
Answer:
The 3 multiples that follow the multiples of 2 and 5 shown on the front of the card are 10, 20, 30.
Explanation:
Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30.
Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50.
Three Least common multiples of 2 and 5 = 10, 20, 30.
A fraction with a numerator that is greater than or equal to the denominator.
Identify this type of fraction: 2\(\frac{4}{5}\). Rewrite it as an improper fraction.
Answer:
2\(\frac{4}{5}\) is mixed fraction.
\(\frac{14}{5}\) is improper fraction of 2\(\frac{4}{5}\).
Explanation:
A fraction represented with its quotient and remainder is a mixed fraction.
2\(\frac{4}{5}\) is mixed fraction.
An improper fraction is a fraction where the numerator is greater than or equal to the denominator.
2\(\frac{4}{5}\)
= [(2 × 5) + 4] ÷ 5
= (10 + 4) ÷ 5
= \(\frac{14}{5}\)
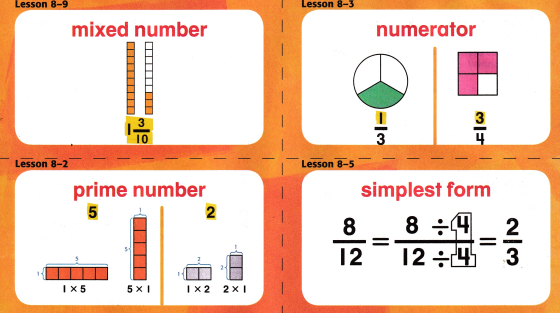
Ideas for Use
- Create cards to review problem-solving strategies, such as work backward.
- Write the name of each lesson on the front of each card. Write a few study tips for each lesson on the back of each card.
The top number in a fraction. It tells how many of the equal parts are being used.
What does the numerator in the following fraction show? \(\frac{9}{20}\)
Answer:
The numerator in the \(\frac{9}{20}\) fraction is 9.
Explanation:
Given fraction = \(\frac{9}{20}\)
Numerator = 9.
Denominator = 20.
A number that has a whole number part and a fraction part.
Explain why a mixed number is called “mixed.”
Answer:
A mixed fraction is a combination of a whole number and a proper fraction that’s why its called as mixed.
Explanation:
A fraction represented with its quotient and remainder is a mixed fraction. For example, 2 1/3 is a mixed fraction, where 2 is the quotient, 1 is the remainder. So, a mixed fraction is a combination of a whole number and a proper fraction.
A fraction in which the numerator and the denominator have no common factor greater than 1.
Write \(\frac{15}{45}\) in its simplest form.
Answer:
Simplest form of \(\frac{15}{45}\) = \(\frac{1}{3}\)
Explanation:
Simplest form:
\(\frac{15}{45}\) ÷ \(\frac{5}{5}\)
= \(\frac{3}{9}\) ÷ \(\frac{3}{3}\)
= \(\frac{1}{3}\)
A whole number with exactly two factors-1 and itself.
Prime comes from the Latin root primus, meaning “first.” How does this help you understand the definition of prime number?
Answer:
A prime number is a whole number greater than 1 whose only factors are 1 and itself by this it helps to understand the definition of prime number.
Explanation:
Prime comes from the Latin root primus, meaning “first.” A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A prime number is a whole number greater than 1 whose only factors are 1 and itself by this it helps to understand the definition of prime number.
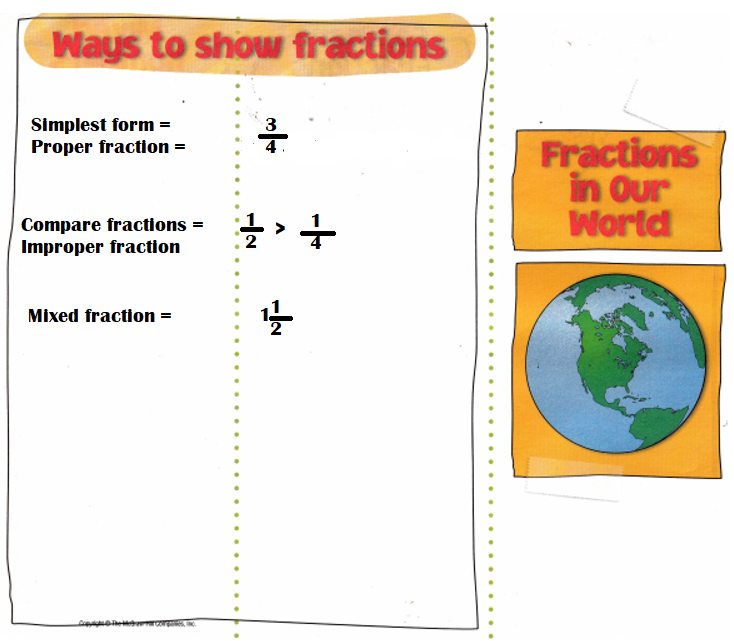
My Foldable
Follow the steps on the back to make your Foldable.


Answer:
Ways to write fractions:
The three major types are proper fractions, improper fractions, and mixed fractions.
Proper fraction = \(\frac{3}{4}\)
Improper fraction = \(\frac{1}{2}\) is greater than \(\frac{1}{4}\)
=> \(\frac{1}{2}\) > \(\frac{1}{4}\)
Mixed fraction: 1\(\frac{1}{2}\)
Explanation:
One number is written above a horizontal line (i.e., 5) and the other is written below it (i.e., 7). The top part is called the numerator and the bottom part is called the denominator. The horizontal line between both the numbers is called the fraction bar.
The three major types are proper fractions, improper fractions, and mixed fractions.
Simplest form = Proper fraction = \(\frac{3}{4}\)
Compare fractions =Improper fraction = \(\frac{1}{2}\) is greater than \(\frac{1}{4}\)
=> \(\frac{1}{2}\) > \(\frac{1}{4}\)
Mixed fraction: 1\(\frac{1}{2}\)