All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 7 Lesson 9 Equations with Multiple Operations will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Answer Key Chapter 7 Lesson 9 Equations with Multiple Operations
You have used tables to show equations with one operation. A table can also help you show equations with two operations.
Math in My World
Example 1
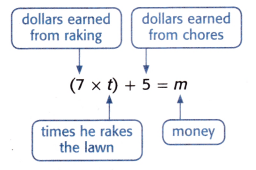
Sam earns $7 each time he rakes his neighbor’s lawn. He also earns $5 each week for doing chores at home. Sam wants to find what he will earn in a week if he does chores and rakes the lawn 1, 2, or 3 times.

1. Write an equation.
2. Complete the table.

So, during one week, if Sam rakes the lawn once, he will earn $ ______________. If he rakes the lawn twice, he will earn $ ______________.
If he rakes the lawn three times, he will earn $ ______________.
Answer:

So, during one week, if Sam rakes the lawn once, he will earn $ 2. If he rakes the lawn twice, he will earn $19.
If he rakes the lawn three times, he will earn $26.
Explanation:
Amount of money Sam earns each time he rakes his neighbor’s lawn = $7.
Amount of money he also earns each week for doing chores at home = $5.
Amount of money he will earn in a week if he does chores and rakes the lawn 1, 2, or 3 times.
Number of times = (t)
Equation:
(Amount of money Sam earns each time he rakes his neighbor’s lawn × Number of times) + Amount of money he also earns each week for doing chores at home = Total amount of money he earned(m)
(7 × t) + 5 = m.
When t = 1,
m = (7 × t) + 5 .
m = (7 × 1) + 5
m = 7 + 5
m = 12.
When t = 2,
m = (7 × t) + 5 .
m = (7 × 2) + 5
m = 14 + 5
m = 19.
When t = 3,
m = (7 × t) + 5 .
m = (7 × 3) + 5
m = 21 + 5
m = 26.
Example 2
Complete the table to find output numbers when x = 2, 3, 4, and 5.

Repeat the process when x = 3, 4, and 5.
When x = 3, y = ______________.
When x = 4, y = ______________.
When x = 5, y = ______________.
Describe patterns you see ¡n the table.
Answer:

It is noticed that the pattern is reducing in the value of output from 1 to 5 of x value.
Explanation:
Equation: 2 × (9 – x) + 3 = y.
When x = 2,
y = 2 × (9 – x) + 3
y = 2 × (9 – 2) + 3
y = 2 × 7 + 3
y = 14 + 3
y = 17.
When x = 3,
y = 2 × (9 – x) + 3
y = 2 × (9 – 3) + 3
y = 2 × 6 + 3
y = 12 + 3
y = 15.
When x = 4,
y = 2 × (9 – x) + 3
y = 2 × (9 – 4) + 3
y = 2 × 5 + 3
y = 10 + 3
y = 13.
When x = 5,
y = 2 × (9 – x) + 3
y = 2 × (9 – 5) + 3
y = 2 × 4 + 3
y = 8 + 3
y = 11.
Talk Math
Explain how tables can help you solve a problem.

Answer:
Making a table helps in organize and clarify the information we were given, and helps in guiding us in the next steps of the problem.
Explanation:
Making a table helps in organize and clarify the information we were given, and helps in guiding us in the next steps of the problem. We solved this problem solely by making a table; in many situations, we would combine this strategy with others to get a solution. It makes easy to understand the problem and to find the solution.
Guided Practice
Question 1.
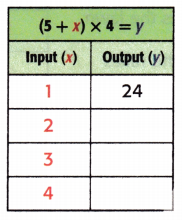
Complete each table.
Answer:
Explanation:
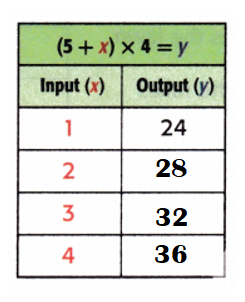
Equation: (5 + x) × 4 = y.
When x = 1;
y = (5 + x) × 4
y = (5 + 1) × 4
y = 6 × 4
y = 24.
When x = 2;
y = (5 + x) × 4
y = (5 + 2) × 4
y = 7 × 4
y = 28.
When x = 3;
y = (5 + x) × 4
y = (5 + 3) × 4
y = 8 × 4
y = 32.
When x = 74
y = (5 + x) × 4
y = (5 + 4) × 4
y = 9 × 4
y = 36.
Independent Practice
Complete each table.
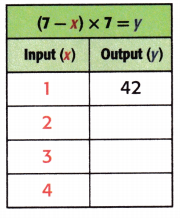
Question 2.
Answer:
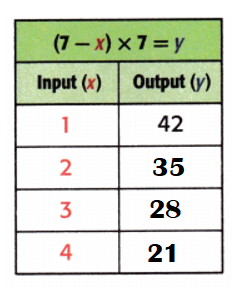
Explanation:
Equation: (7 – x) × 7 = y
When x = 2;
y = (7 – x) × 7
y = (7 – 2) × 7
y = 5 × 7
y = 35.
When x = 3;
y = (7 – x) × 7
y = (7 – 3) × 7
y = 4 × 7
y = 28.
When x = 4;
y = (7 – 4) × 7
y = (7 – 4) × 7
y = 3 × 7
y = 21.
Question 3.
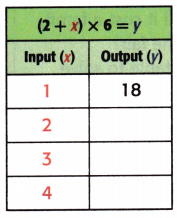
Answer:
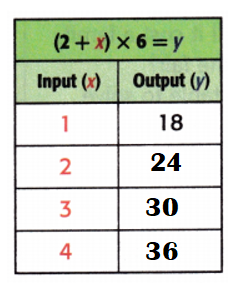
Explanation:
Equation: (2 + x) × 6 = y.
When x = 2;
y = (2 + x) × 6
y = (2 + 2) × 6
y = 4 × 6
y = 24.
When x = 3;
y = (2 + 3) × 6
y = 5 × 6
y = 30.
When x = 4;
y = (2 + 4) × 6
y = 6 × 6
y = 36.
Question 4.
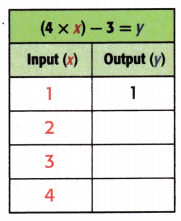
Answer:
Explanation:
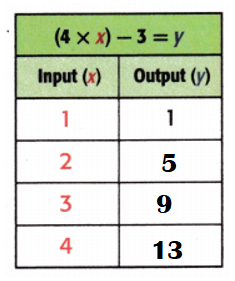
Equation: (4 × x) – 3 = y.
When x = 2;
y = (4 × x) – 3
y = (4 × 2) – 3
y = 8 – 3
y = 5.
When x = 3;
y = (4 × x) – 3
y = (4 × 3) – 3
y = 12 – 3
y = 9.
When x = 4;
y = (4 × x) – 3
y = (4 × 4) – 3
y = 16 – 3
y = 13.
Question 5.
Answer:
Explanation:
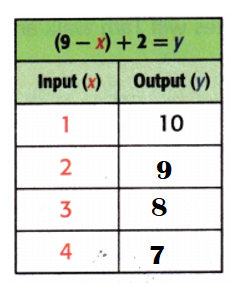
Equation: (9 – x) + 2 = y
When x = 2;
y = (9 – x) + 2
y = (9 – 2) + 2
y = 7 + 2
y = 9.
When x = 3;
y = (9 – x) + 2
y = (9 – 3) + 2
y = 6 + 2
y = 8.
When x = 4;
y = (9 – x) + 2
y = (9 – 4) + 2
y = 5 + 2
y = 7.
Question 6.
Answer:
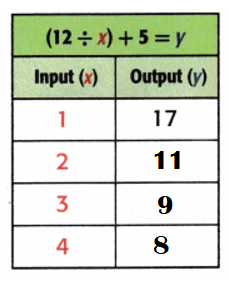
Explanation:
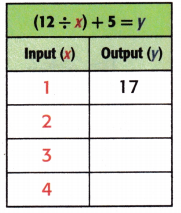
Equation: (12 ÷ x) + 5 = y.
When x = 2;
y = (12 ÷ x) + 5
y = (12 ÷ 2) + 5
y = 6 + 5
y= 11.
When x = 3;
y = (12 ÷ x) + 5
y = (12 ÷ 3) + 5
y = 4 + 5
y = 9.
When x = 4;
y = (12 ÷ x) + 5
y = (12 ÷ 4) + 5
y = 3 + 5
y = 8.
Question 7.
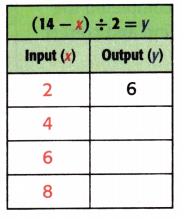
Answer:
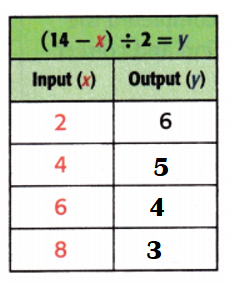
Explanation:
Equation: (14 – x) ÷ 2 = y.
When x = 4;
y = (14 – x) ÷ 2
y = (14 – 4) ÷ 2
y = 10 ÷ 2
y = 5.
When x = 6;
y = (14 – x) ÷ 2
y = (14 – 6) ÷ 2
y = 8 ÷ 2
y = 4.
When x = 8;
y = (14 – x) ÷ 2
y = (14 – 8) ÷ 2
y = 6 ÷ 2
y = 3.
Question 8.
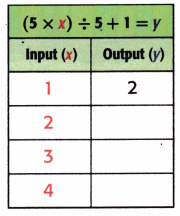
Answer:
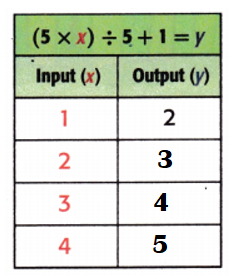
Explanation:
Equation: (5 × x) ÷ 5 + 1 = y.
When x = 2;
y = (5 × x) ÷ 5 + 1
y = (5 × 2) ÷ 5 + 1
y = 10 ÷ 5 + 1
y = 2 + 1
y = 3.
When x = 3;
y = (5 × x) ÷ 5 + 1
y = (5 × 3) ÷ 5 + 1
y = 15 ÷ 5 + 1
y = 3 + 1
y = 4.
When x = 4;
y = (5 × x) ÷ 5 + 1
y = (5 × 4) ÷ 5 + 1
y = 20 ÷ 5 + 1
y = 4 + 1
y = 5.
Question 9.

Answer:
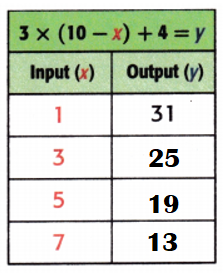
Explanation:
Equation: 3 × (10 – x) + 4 = y.
When x = 3;
y = 3 × (10 – x) + 4
y = 3 × (10 – 3) + 4
y = 3 × 7 + 4
y = 21 + 4
y = 25.
When x = 5;
y = 3 × (10 – x) + 4
y = 3 × (10 – 5) + 4
y = 3 × 5 + 4
y = 15 + 4
y = 19.
When x = 7;
y = 3 × (10 – x) + 4
y = 3 × (10 – 7) + 4
y = 3 × 3 + 4
y = 9 + 4
y = 13.
Problem Solving
Question 10.
Mathematical PRACTICE Use Math Tools It costs $3 to park at the fair. Tickets cost $6 each. How much will it cost a family of 4 to go to the fair? Complete the table to solve.
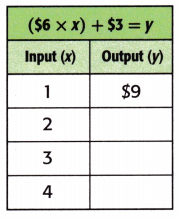
Answer:
Total cost a family of 4 to go to the fair = $27.
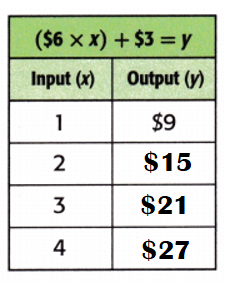
Explanation:
Cost to park at the fair = $3.
Cost of each ticket = $6.
Number of people = 4.
Total cost a family of 4 to go to the fair = (Cost of each ticket × Number of people) + Cost to park at the fair
= ($6 × 4) + $3
= $24 + $3
= $27.
Equation: ($6 × x) + $3 = y.
When x = 2;
y = ($6 × x) + $3
y = ($6 × 2) + $3
y = $12 + $3
y = $15.
When x = 3;
y = ($6 × x) + $3
y = ($6 × 3) + $3
y = $18 + $3
y = $21.
Question 11.
Tam walks 2 miles to school each day. During gym class, she always runs three times as far as Dante. How many miles will Tam walk and run if Dante runs 1 mile?
Answer:
Total number of miles Tam walk and run if Dante runs 1 mile = 5.
Explanation:
Number of miles Tam walks to school each day = 2.
During gym class, she always runs three times as far as Dante.
Number of miles she runs during gym be x.
Total number of miles Tam walk and run if Dante runs 1 mile = Number of miles Tam walks to school each day + 3(Number of miles she runs during gym be)
= 2 + 3(1)
= 2 + 3
= 5.
HOT Problems
Question 12.
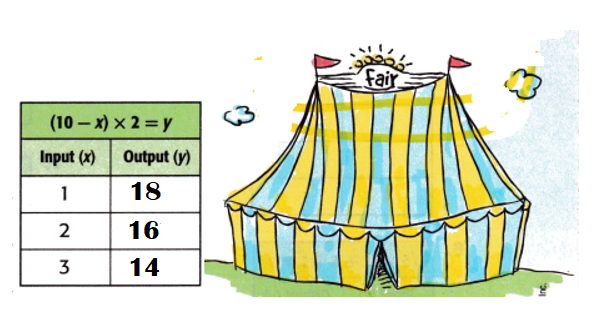
Mathematical PRACTICE Find the Error Ashley completed the table shown. Find and correct her mistake.

Answer:
The mistake Ashley did is that she did addition instead of multiplication.

Correct table:
Explanation:
Equation: (10 – x) × 2 = y.
When x = 1;
y = (10 – x) × 2
y = (10 – 1) × 2
y = 9 × 2
y = 18.
When x = 2;
y = (10 – x) × 2
y = (10 – 2) × 2
y = 8 × 2
y = 16.
When x = 3;
y = (10 – x) × 2
y = (10 – 3) × 2
y = 7 × 2
y = 14.
The mistake Ashley did is that she did addition instead of multiplication.
Question 13.
Building on the Essential Question Describe a real-world situation that could use a table with two operations.
Answer:
We will see tables in use when shopping for cell phone plans and will see graphs in use when you research population growth. Both are used to present real data.
Explanation:
Price list of cell phones in shopping and population growth data…
We will see tables in use when shopping for cell phone plans and will see graphs in use when you research population growth. Both are used to present real data. In algebra, both are used as visual representations of functions and data.
McGraw Hill My Math Grade 4 Chapter 7 Lesson 9 My Homework Answer Key
Practice
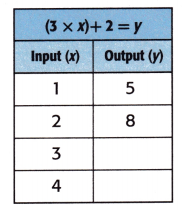
Question 1.
Complete the table.
Answer:
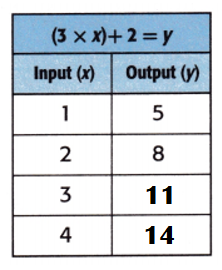
Explanation:
Equation: (3 × x) + 2 = y.
When x = 3;
y = (3 × x) + 2
y = (3 × 3) + 2
y = 9 + 2
y = 11.
When x = 4;
y = (3 × x) + 2
y = (3 × 4) + 2
y = 12 + 2
y = 14.
Complete each table.
Question 2.
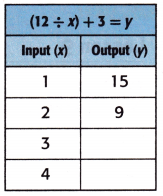
Answer:
Explanation:
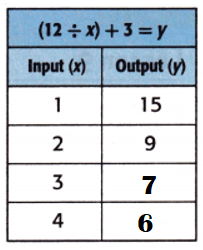
Equation: (12 ÷ x) + 3 = y.
When x = 3;
y = (12 ÷ x) + 3
y = (12 ÷ 3) + 3
y = 4 + 3
y = 7.
When x = 4;
y = (12 ÷ x) + 3
y = (12 ÷ 4) + 3
y = 3 + 3
y = 6.
Question 3.
Answer:
Explanation:
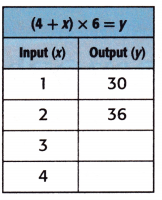
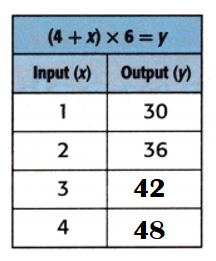
Equation: (4 + x) × 6 = y.
When x = 3;
y = (4 + x) × 6
y = (4 + 3) × 6
y = 7 × 6
y = 42.
When x = 4;
y = (4 + x) × 6
y = (4 + 4) × 6
y = 8 × 6
y = 48.
Question 4.
Answer:
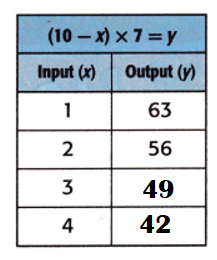
Explanation:
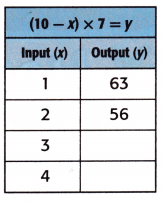
Equation: (10 – x) × 7 = y.
When x = 3;
y = (10 – x) × 7
y = (10 – 3) × 7
y = 7 × 7
y = 49.
When x = 4;
y = (10 – x) × 7
y = (10 – 4) × 7
y = 6 × 7
y = 42.
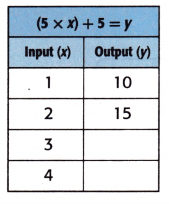
Question 5.
Answer:
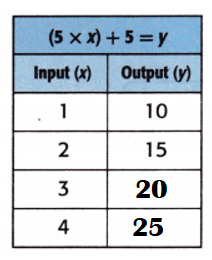
Explanation:
Equation: (5 × x) + 5 = y.
When x = 3;
y = (5 × x) + 5
y = (5 × 3) + 5
y = 15 + 5
y = 20.
When x = 4;
y = (5 × x) + 5
y = (5 × 4) + 5
y = 20 + 5
y = 25.
Question 6.
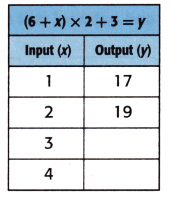
Answer:
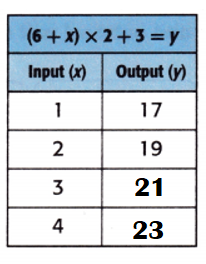
Explanation:
Equation: (6 + x) × 2 + 3 = y.
When x = 3;
y = (6 + x) × 2 + 3
y = (6 + 3) × 2 + 3
y = 9 × 2 + 3
y = 18 + 3
y = 21.
When x = 4;
y = (6 + x) × 2 + 3
y = (6 + 4) × 2 + 3
y = 10 × 2 + 3
y = 20 + 3
y = 23.
Question 7.
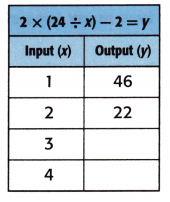
Answer:
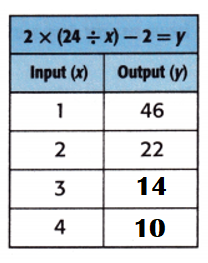
Explanation:
Equation: 2 × (24 ÷ x) – 2 = y.
When x = 3;
y = 2 × (24 ÷ x) – 2
y = 2 × (24 ÷ 3) – 2
y = 2 × 8 – 2
y = 16 – 2
y = 14.
When x = 4;
y = 2 × (24 ÷ x) – 2
y = 2 × (24 ÷ 4) – 2
y = 2 × 6 – 2
y = 12 – 2
y = 10.
Problem Solving
Question 8.
Mathematical PRACTICE Make Sense of Problems Mauricio hits a baseball 4 times as often as Tony each game. He also hits 20 baseballs every Monday at practice. How many baseballs will Mauricio hit this week if Tony hits 4 balls at the game Saturday?
Answer:
Number of baseballs will Mauricio hit this week if Tony hits 4 balls at the game Saturday = 36.
Explanation:
Mauricio hits a baseball 4 times as often as Tony each game.
Number of times Mauricio hits a baseball = 4 times.
Number of baseballs every Monday at practice he hits = 20.
Number of baseballs Tony hits 4 balls at the game Saturday = 4.
Number of baseballs will Mauricio hit this week if Tony hits 4 balls at the game Saturday = (4 × Number of baseballs Tony hits 4 balls at the game Saturday) + Number of baseballs every Monday at practice he hits
= (4 × 4) + 20
= 16 + 20
= 36.
Question 9.
Callie loves flowers. She picks 4 tulips for every daisy she picks. Callie’s mom also gave her 6 tulips this week from her garden. How many tulips will Callie have this week if she picks 3 daisies?
Answer:
Number of tulips will Callie have this week if she picks 3 daisies = 18.
Explanation:
Number of tulips she picks for every daisy = 4.
Number of tulips Callie’s mom also gave her this week from her garden = 6.
Number of tulips will Callie have this week if she picks 3 daisies = (3 × Number of tulips she picks for every daisy) + Number of tulips Callie’s mom also gave her this week from her garden
= (3 × 4) + 6
= 12 + 6
= 18.
Test Practice
Question 10.
Refer to the equation (x × 3) – 2 = y. If x = 7, what is the value of y?
(A) y = 27
(B) y = 23
(C) y = 21
(D) y = 19
Answer:
Equation: (x × 3) – 2 = y.
When x = 7, y = 19.
Explanation:
Equation: (x × 3) – 2 = y.
When x = 7;
y = (x × 3) – 2
y = (7 × 3) – 2
y = 21 – 2
y = 19.