All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 7 Lesson 6 Multiplication and Division Rules will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Answer Key Chapter 7 Lesson 6 Multiplication and Division Rules
You can write a multiplication or division equation to extend a pattern.
Math in My World
Example 1
Charles washes cars to earn money. if he washes 2 cars, he earns $12. if he washes 6 cars, he earns $36. Write an equation to describe the pattern. Then use the equation to find how much money Charles will earn if he washes 8, 10, and 12 cars.

Complete the table. Then look for the pattern that describes a rule.
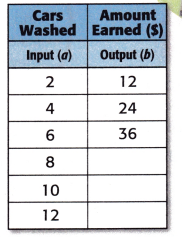
Pattern:
2 × _____________ = 12
4 × _____________ = 24
6 × _____________ = 36
Rule: Multiply by ____________.
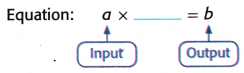
Find the next three output numbers when the input a is 8, 10, and 12.
So, Charles will earn $___________ , $___________ , and $_____________.
Answer:
Number of cars × 6 = Amount paid.
=> Input × 6 = Output.
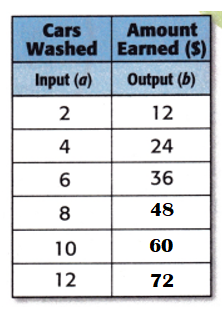
So, Charles will earn $48, $60, and $72.
Explanation:
Number of cars he washes = 2.
Amount of money he gets for washing two cars = $12.
Amount of money he gets for washing one car = Amount of money he gets for washing two cars ÷ Number of cars he washes
= $12 ÷ 2
= $6.
Multiplication Equation:
Number of cars × 6 = Amount paid.
=> Input × 6 = Output.
4 × 6 = 24.
6 × 6 = 36.
8 × 6 = 48.
10 × 6 = 60.
12 × 6 = 72.
Example 2
It costs $4 for each box of crackers. The equation is shown below. Use the equation to complete the table.
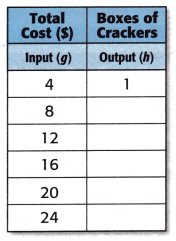
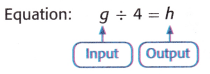
Rule: Divide by 4.
Find the next five output numbers when the input g is 8, 12, 16, 20, and 24.
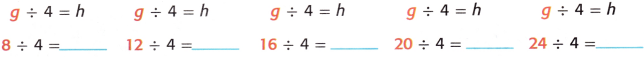
So, the next five output numbers are _______________
Describe another pattern you see in this table.
Answer:
Division Equation:
Total cost ÷ Cost of each box of crackers = Boxes of crackers.
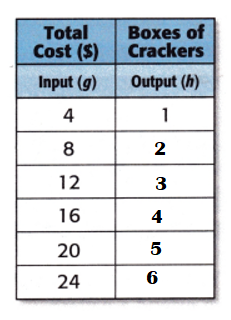
Explanation:
It costs $4 for each box of crackers.
Division Equation:
Total cost ÷ Cost of each box of crackers = Boxes of crackers.
=> Input ÷ Cost of each box of crackers = Output
4 ÷ 4 = 1.
8 ÷ 4 = 2.
12 ÷ 4 = 3.
16 ÷ 4 = 4.
20 ÷ 4 = 5.
24 ÷ 4 = 6.
Talk Math
How are a rule and an equation alike? How are they different?

Answer:
They are different as rules are many to form where as for an equation there has to be a condition of statement. They are almost similar as both are expressions.
Explanation:
An algebraic rule is a mathematical expression that relates two variables and is written in the form of an equation. There are many constant algebraic rules, such as area = length x width.
An equation is a mathematical statement that is made up of two expressions connected by an equal sign. For example, 3x – 5 = 16 is an equation.
They are different as rules are many to form where as for an equation there has to be a condition of statement. They are almost similar as both are expressions.
Guided Practice
Question 1.
Write an equation that describes the pattern. Then use the equation to find the next three output numbers.
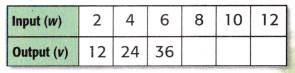
Equation: ______________
Describe a pattern you see in this chart.
Answer:
Equation: Output ÷ 6 = Input.
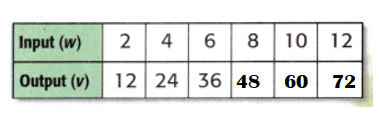
Explanation:
Output ÷ ?? = Input.
=> 12 ÷ ?? = 2.
=> 12 ÷ 2 = ??
=> 6 = ??
Equation: Output ÷ 6 = Input.
24 ÷ 6 = 4.
36 ÷ 6 = 6
??÷ 6 = 8
=> ?? = 8 × 6
=> ?? = 48.
?? ÷ 6 = 10.
=> ?? = 10 × 6
=> ?? = 60.
?? ÷ 6 = 12
=> ?? = 12 × 6
=> ?? = 72.
McGraw Hill My Math Grade 4 Chapter 7 Lesson 6 My Homework Answer Key
Practice
Write an equation that describes the pattern. Then use the equation to find the next three output numbers.
Question 1.
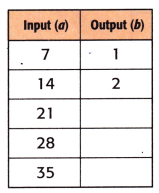
Equation: ______________
Answer:
Equation: Input ÷ 7 = Output.
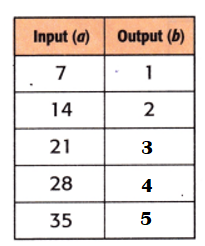
Explanation:
Input ÷ ?? = Output.
7 ÷ ?? = 1.
=> 7 ÷ 1 = ??
=> 7 = ??.
Equation: Input ÷ 7 = Output.
14 ÷ 7 = 2.
21 ÷ 7 = 3.
28 ÷ 7 = 4.
35 ÷ 7 = 5.
Question 2.
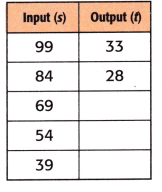
Equation: ______________
Answer:
Equation: Input ÷ 3 = Output.
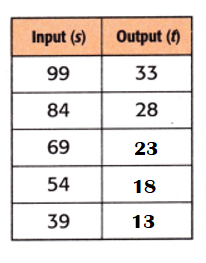
Explanation:
Input ÷ ?? = Output.
99 ÷ ?? = 33.
=> 99 ÷ 33 = ??
=> 3 = ??.
Equation: Input ÷ 3 = Output.
84 ÷ 3 = 28.
69 ÷ 3 = 23.
54 ÷ 3 = 18.
39 ÷ 3 = 13.
Question 3.
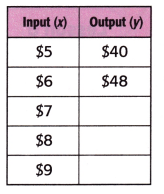
Equation: ______________
Answer:
Equation: Input × $8 = Output.
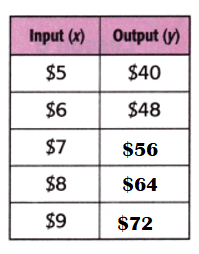
Explanation:
Input ÷ ?? = Output.
$5 ÷ ?? = $40.
=> $40 ÷ $5 = ??
=> $8 = ??.
Equation: Input × $8 = Output.
$5 × $8 = $40.
$6 × $8 = $48.
$7 × $8 = $56.
$8 × $8 = $64.
$9 × $8 = $72.
Question 4.
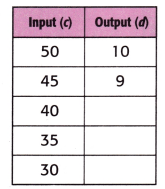
Equation: ______________
Answer:
Equation: Input ÷ 5 = Output.
Explanation:
Input ÷ ?? = Output.
50 ÷ ?? = 10.
=> 50 ÷ 10 = ??
=> 5 = ??.
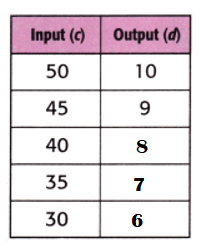
Equation: Input ÷ 5 = Output.
45 ÷ 5 = 9.
40 ÷ 5 = 8.
35 ÷ 5 = 7.
30 ÷ 5 = 6.
Problem Solving
Shawna found out there are 4 yellow pencils for every blue pencil.
Question 5.
Mathematical PRACTICE Use Algebra Write an equation for this situation.
Answer:
Equation: Number of yellow pencils ÷ 4 = Blue pencil.
Input ÷ 4 = Output.
Explanation:
Shawna found out there are 4 yellow pencils for every blue pencil.
Number of yellow pencils ÷ ?? = Blue pencil.
4 ÷ ?? = 1.
=> 4 ÷ 1 = ??
=> 4 = ??.
Equation: Number of yellow pencils ÷ 4 = Blue pencil.
Input ÷ 4 = Output.
Question 6.
Complete the table to show how many yellow pencils there are if there are 5, 7, 9, 11, or 13 blue pencils.
Answer:
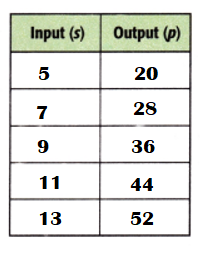
Explanation:
Equation: Number of yellow pencils ÷ 4 = Blue pencil.
Blue pencil × 4 = Number of yellow pencils.
5 × 4 = 20.
7 × 4 = 28.
9 × 4 = 36.
11 × 4 = 44.
13 × 4 = 52.
Test Practice
Question 7.
Refer to the equation a × 9 = b. If a = 3, what is the value of b?
(A) 3
(B) 12
(C) 18
(D) 27
Answer:
The value of b = 27.
(D) 27.
Explanation:
Equation a × 9 = b.
If a = 3,
=> 3 × 9 = 27.