All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 7 Check My Progress will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Chapter 7 Check My Progress Answer Key
Check My Progress Page No. (437 – 438)
Vocabulary Check
Identify each pattern as a nonnumeric pattern or a numeric pattern.
Question 1.
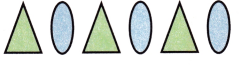
Answer:
It is a nonnumeric pattern.
Explanation:
A nonnumeric pattern is a pattern often using shapes or symbols.

Question 2.
43, 46, 47, 50, 51, 54, 55
Answer:
43, 46, 47, 50, 51, 54, 55 is a numerical pattern.
Explanation:
A numerical pattern is a sequence of numbers that has been created based on a rule called a pattern rule.
43, 46, 47, 50, 51, 54, 55
Question 3.
98, 88, 78, 68, 58, 48
Answer:
98, 88, 78, 68, 58, 48 is a numerical pattern.
Explanation:
A numerical pattern is a sequence of numbers that has been created based on a rule called a pattern rule.
Question 4.
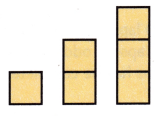
Answer:
It is a nonnumeric pattern.
Explanation:
A nonnumeric pattern is a pattern often using shapes or symbols.

Use the pattern below for Exercises 5-7.
2, 6, 18, 54, 162
Question 5.
Put a circle around one term in the pattern.
Answer:
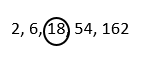
Explanation:
2, 6, 18, 54, 162
One term in the pattern to circle:
2 × 3 = 6.
18 × 3 = 54.
162 × 3 = 486.
Question 6.
Underline the sequence.
Answer:
Sequence is underlined:
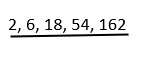
Explanation:
A sequence is an ordered list of numbers.
Question 7.
Write the rule for this pattern.
Answer:
The rule for this pattern is all numbers multiplied by 3.
Explanation:
2, 6, 18, 54, 162.
Rule:
2 × 3 = 6.
6 × 3 = 18.
18 × 3 = 54.
54 × 3 = 162.
Concept Check
Question 8.
Extend the pattern. Draw the shapes on the lines.

Answer:

Explanation:
Next shape on the lines = circle and square.
Question 9.
Identify, describe, and extend each pattern.
3, 8, 13, 18, 23, _____________
The pattern is _____________.
Answer:
3, 8, 13, 18, 23,
The pattern is numerical pattern.
Explanation:
3, 8, 13, 18, 23,
A numerical pattern is a sequence of numbers that has been created based on a rule called a pattern rule.
Question 10.
Extend the pattern below by four terms. Write an observation about the pattern.
Rule: subtract 6
Pattern: 76, _______, ________, ________, __________
Observation: _____________
Answer:
Rule: subtract 6
Pattern: 76, 70, 64, 58, 52.
It is observed all numbers have 6 difference and are even numbers.
Explanation:
Rule: subtract 6
Pattern: 76, 70, 64, 58, 52.
76 – 6 = 70.
70 – 6 = 64.
64 – 6 = 58.
58 – 6 = 52.
All numbers have 6 difference and are even numbers.
Problem Solving
Question 11.
On Mondays, Wednesdays, and Fridays, Luke packs his lunch. On Tuesdays and Thursdays, Luke buys his lunch. Draw a nonnumeric pattern to show the pattern of Luke’s lunch for two weeks.
Answer:
The non-numeric pattern that shows the pattern of Luke’s lunch for two weeks = P B P B P P B P B P
Explanation:
Number of days Luke packs his lunch (P)= 3.
Number of days Luke buys his lunch (B) = 2.
The non-numeric pattern that shows the pattern of Luke’s lunch for two weeks can be represented as:
Mon Tues Wed Thurs Fri Mon Tues Wed Thurs Fri
P B P B P P B P B P
Question 12.
Bob swims 10 laps on even numbered dates. He swims 15 laps on odd numbered dates. How many laps has he completed by the sixth of the month?
Answer:
Total numbers of laps he has completed by the sixth of the month = 75.
Explanation:
Number of laps on even numbered dates Bob swims = 10.
Number of laps on odd numbered dates Bob swims = 15.
Number of days from 1 to 6= 6 [3 even number days (2,4,6) and 3 odd number days (1,3,5)].
Total numbers of laps he has completed by the sixth of the month = 3 (Number of laps on even numbered dates Bob swims) + 3(Number of laps on odd numbered dates Bob swims)
=> 3(10) + 3(15)
=> 30 + 45
=> 75 laps.
Test Practice
Question 13.
A nonnumeric pattern is shown below.

Which shows the next three objects in the pattern?
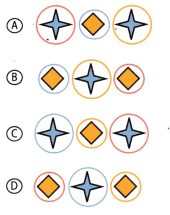
Answer:
Next three objects in the pattern:
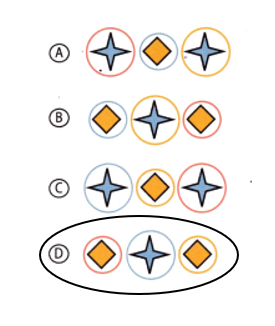
Explanation:

Next three objects in the pattern = square, star, square.
Check My Progress Page No. (457 – 458)
Vocabulary Check
Use the words in the word bank to complete each sentence.
equation
input
operation
output
unknown
Question 1.
In the equation 4 + x = 7, the variable x is a(n) ______________.
Answer:
In the equation 4 + x = 7, the variable x is a(n) unknown.
Explanation:
Equation 4 + x = 7,
the variable x is a(n) unknown as its value has to be found.
Question 2.
In the table to the right, the letter m represents the ______________. The letter n represents the _____________.
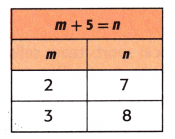
Answer:
In the table to the right, the letter m represents the input. The letter n represents the output.
Explanation:
In the table: to the right – the input.
to the left – the output always it represents.
Question 3.
A(n) ______________ that contains an equals sign (=), showing that two expressions are equal.
Answer:
A(n) equation that contains an equals sign (=), showing that two expressions are equal.
Explanation:
An equation is a mathematical statement that is made up of two expressions connected by an equal sign. For Example: 3x – 5 = 16 is an equation.
Question 4.
Addition is an example of a(n) ________________.
Answer:
Addition is an example of a(n) operation.
Explanation:
An operation is a mathematical action. Addition, subtraction, multiplication, division, and calculating the root are all examples of a mathematical operation.
Concept Check
Write an equation that describes the pattern. Then use the equation to find the next three output numbers.
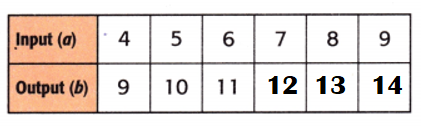
Question 5.
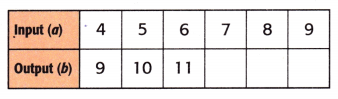
Equation: ________________
Answer:
Equation: a + 5 = b.
Explanation:
Equation: a + 5 = b.
When a = 6:
b = a + 5
b = 6 + 5
b = 11.
When a = 7:
b = a + 5
b = 7 + 5
b = 12.
When a = 8:
b = a + 5
b = 8 + 5
b = 13.
When a = 9:
b = a + 5
b = 9 + 5
b = 14.
Question 6.
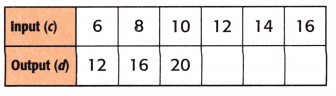
Equation: ________________
Answer:
Equation: c × 2 = d.
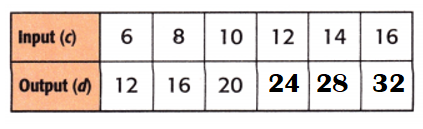
Explanation:
Equation: c × 2 = d.
When c = 12;
d = c × 2
d = 12 × 2
d = 24.
When c = 14;
d = c × 2
d = 14 × 2
d = 28.
When c = 16;
d = c × 2
d = 16 × 2
d = 32.
Find the value of each expression.
Question 7.
(7 + 5) ÷ 3 = ______________
Answer:
The value of (7 + 5) ÷ 3 expression = 4.
Explanation:
Expression: (7 + 5) ÷ 3
= 12 ÷ 3
= 4.
Question 8.
11 – 2 × 5 = _______________
Answer:
The value of 11 – 2 × 5 expression = 45.
Explanation:
Expression: 11 – 2 × 5
= 9 × 5
= 45.
Problem Solving
Question 9.
The amount in dollars c a bus company charges to take s students on a field trip are shown at the right. Write an equation to describe the pattern. Then complete the table to show how much it would cost for 40 and 50 students to go on a field trip.
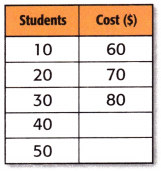
Answer:
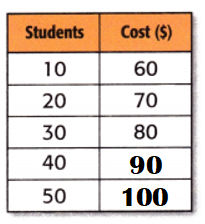
Explanation:
Number of students on on a field trip = s.
Amount of money a bus company charges = $c.
Equation:
Amount of students on a field trip before + $10 = c.
When s = 40;
c = $80 + $10
c = $90.
When s = 50;
c = $90 + $10
c = $100.
Question 10.
A local sports team sells 6 tickets for $3, 8 tickets for $4, and 10 tickets for $5. Write a rule and equation to find the cost of 20 tickets.
Answer:
Cost of 20 tickets = $10.
Explanation:
Number of tickets a local sports team sells = 6.
Cost of 6 tickets = $3.
Cost of 8 tickets = $4.
Cost of 10 tickets = $5.
Number of (t) tickets × ($1) ÷ 2 = Cost of (t) tickets.
=> 20 ÷ 2 = Cost of 20 tickets.
=> $10 = Cost of 20 tickets.
Question 11.
Each peanut butter snack costs $2. Each chocolate snack costs $3. How much does it cost to buy 6 peanut butter snacks and 8 chocolate snacks? Write an equation.
Answer:
Cost of 6 peanut butter snacks and 8 chocolate snacks = $36.
Explanation:
Cost of each peanut butter snack = $2.
Number of peanut butter snack = 6.
Cost of each chocolate snack = $3.
Number of chocolate snacks = 8.
Cost of 6 peanut butter snacks and 8 chocolate snacks = (Cost of each peanut butter snack × Number of peanut butter snack) + (Cost of each chocolate snack × Number of chocolate snacks)
= ($2 × 6) + ($3 × 8)
= $12 + $24
= $36.
Test Practice
Question 12.
What is the value of m in the equation to the right if n = 6?
9 × n = m
(A) 15
(B) 27
(C) 54
(D) 81
Answer:
Equation: 9 × n = m.
When n = 6; m = 54.
(C) 54
Explanation:
Equation: 9 × n = m.
When n = 6;
m = 9 × n
m = 9 × 6
m = 54.