All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 14 Lesson 7 Solve Problems with Angles will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Answer Key Chapter 14 Lesson 7 Solve Problems with Angles
An angle can be decomposed, or broken, into non-overlapping parts. The angle measure of the whole is the sum of the angle measures of the parts.
Math in My World
Example 1
Rachel and Dean made a sign out of fabric like the one shown to hang in the school gymnasium. The blue piece has a 35° Angle. The red piece is attached to the longest side of the blue piece. Together. the pieces form a right angle. What is the angle shown on the red piece?

One Way: Make a model.
Draw a 90° angle. Mark off a 35° angle. Measure the other angle.
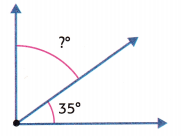
The other angle has a measure of ____________.
Answer: 55 degrees
Another Way: Use an equation.
The 90° angle measure is the sum of two parts. One angle is 35°. Find the unknown angle measure.
Let r represent the unknown angle measure.
35 + r = 90
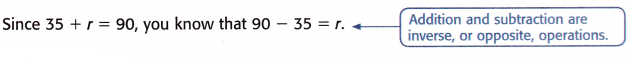
r = 90 – 35
r = ______________
So, the angle shown on the red piece measures _____________.
Answer: 55 degrees
Example 2
Find the combined measure of the angle shown.
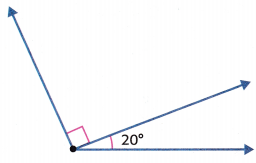
One of the angles is 20°. The symbol on the other angle shows that it is a right angle. Therefore, it is 90°.
To find the combined measure of the angle, add the angle measures of the parts.
Let a represent the combined angle measure.
a = 20° + 90°
a = ______________
So, the combined measure of the angle is _______________.
Answer:
a = 20° + 90°
a = 110°
So, the combined measure of the angle is 110 degrees
Guided Practice
Algebra Find each unknown.
Question 1.
The combined angle measure is 90°.
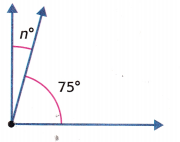
n = ______________
Answer: 15 degrees
The 90° angle measure is the sum of two parts. One angle is 75°.
Let n represent the unknown angle measure.
75 + n = 90
n= 90 – 75 = 15 degrees
Question 2.
The combined angle measure is 130°.
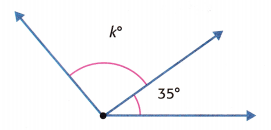
k = ______________
Answer: 95 degrees
The 130° angle measure is the sum of two parts. One angle is 35°.
Let k represent the unknown angle measure.
k + 35 = 130
k = 130 – 35 = 95 degrees
Question 3.
Find the combined angle measure.
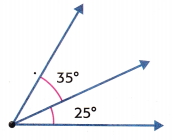
combined measure = _____________
Answer: 60 degrees
To find the combined measure of the angle, add the angle measures of the parts.
Let a represent the combined angle measure.
a = 25° + 35°
a = 60 degrees
Talk Math
How can the measures of parts of an angle be used to find the combined measure?

Answer: Combined measure is possible with adjacent angles. Two angles that are next to each other without overlapping are called Adjacent angles. These angles can be added together to make a larger angle. In order to get the combined measure of an angle, calculate the individual angles and simply perform addition. Adding angles is the same as adding numbers. We can add two or more angles as long as they are not overlapping.
Independent Practice
Algebra Find each unknown.
Question 4.
The combined angle measure is 50°.
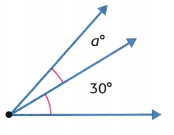
a = ______________
Answer: 20 degrees
The combined angle measure is 50°. The 50° angle measure is the sum of two parts. One angle is 30°.
Let a represent the unknown angle measure.
a + 30 = 50
a = 50 – 30 = 20 degrees
Question 5.
The combined angle measure is 90°.
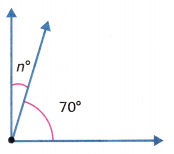
n = _______________
Answer: 20 degrees
The combined angle measure is 90°. The 90° angle measure is the sum of two parts. One angle is 70°.
Let n represent the unknown angle measure.
n + 70 = 90
n = 90 – 70 = 20 degrees
Question 6.
The combined angle measure is 125°.
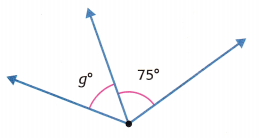
g = ________________
Answer: 50 degrees
The combined angle measure is 125°. The 125° angle measure is the sum of two parts. One angle is 75°.
Let g represent the unknown angle measure.
g + 75 = 125
g = 125 – 75 = 50 degrees
Question 7.
The combined angle measure is 150°.
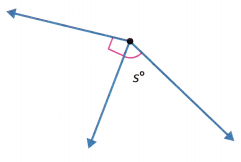
s = ________________
Answer: 60 degrees
The combined angle measure is 150°. The 150° angle measure is the sum of two parts. One angle is 90°.
Let s represent the unknown angle measure.
s + 90 = 150
s = 150 – 90 = 60 degrees
Question 8.
Draw a triangle with one right angle.
Find the combined measure of the three angles.
Answer:
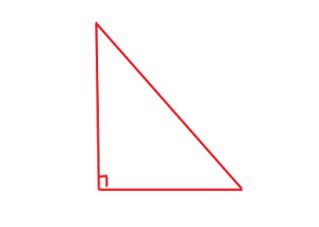
For any triangle, the sum of all the interior angles is equal to 180 degrees. For a right angle triangle, one of the angle is 90 degrees. So the combined angle of other two angles is 180 – 90 = 90 degrees.
Question 9.
Draw a triangle with one obtuse angle.
Find the combined measure of the three angles.
Answer:
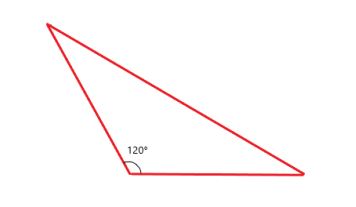
For any triangle, the sum of all the interior angles is equal to 180 degrees. To draw an obtuse angle triangle, we choose 120 degrees as one of the angles in the triangle. So the combined angle of other two angles is 180 – 120 = 60 degrees.
Problem Solving
Question 10.
The steps on a staircase should be 90°. One of the steps is crooked. The angle formed is 15° too large. What is the angle of that step?
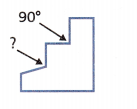
Answer: 105 degrees
The steps on a staircase should be 90°.
The angle formed by the crooked step is 15 degrees more.
Therefore, the angle of that crooked step = 90 + 15 = 105 degrees.
Question 11.
Mathematical PRACTICE Model Math The combined measure of the angles is 150°. One angle measures 50°. Find the value of x.
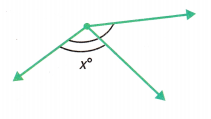
Answer: 100 degrees
The combined angle measure is 150°. The 150° angle measure is the sum of two parts. One angle is 50°.
Let x represent the unknown angle measure.
x + 50 = 150
x = 150 – 50 = 100 degrees
HOT Problems
Question 12.
Mathematical PRACTICE Understand Symbols Find the value of k.
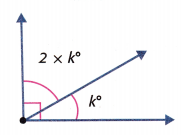
k = ______________
Answer: 30 degrees
The combined angle measure is 90°, as the figure is right angle. 2k and k are both angles used to form 90 degrees
Therefore, 2k + k = 90
3k = 90
k = 30 degrees
Question 13.
Building on the Essential Question How is addition related to angle measurement?
Answer: Two angles that are next to each other without overlapping are called Adjacent angles. These angles can be added together to make a larger angle. Adding angles is the same as adding numbers. We can add two or more angles as long as they are not overlapping.
McGraw Hill My Math Grade 4 Chapter 14 Lesson 7 My Homework Answer Key
Practice
Algebra Find each unknown.
Question 1.
The combined angle measure is 50°.
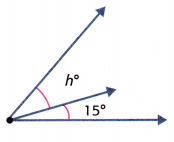
h = _____________
Answer: 35 degrees
The combined angle measure is 50°. The 50° angle measure is the sum of two parts. One angle is 15°.
Let h represent the unknown angle measure.
h + 15 = 50
h = 50 – 15 = 35 degrees
Question 2.
The combined angle measure is 135°.
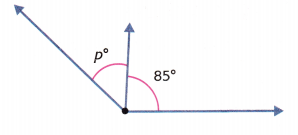
p = _______________
Answer: 50 degrees
The combined angle measure is 135°. The 135° angle measure is the sum of two parts. One angle is 85°.
Let p represent the unknown angle measure.
p + 85 = 135
p = 135 – 85 = 50 degrees
Question 3.
The combined angle measure is 70°.
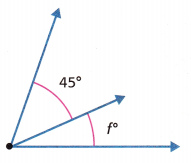
f = _________________
Answer: 25 degrees
The combined angle measure is 70°. The 70° angle measure is the sum of two parts. One angle is 45°.
Let f represent the unknown angle measure.
f + 45 = 70
f = 70 – 45 = 25 degrees
Question 4.
The combined angle measure is 115°.
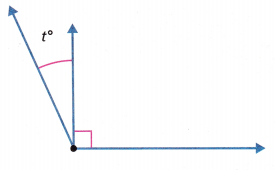
t = _________________
Answer: 25 degrees
The combined angle measure is 115°. The 115° angle measure is the sum of two parts. One angle is 90°.
Let t represent the unknown angle measure.
t + 90 = 115
t = 115 – 90 = 25 degrees
Question 5.
The combined angle measure is 180°.
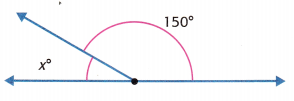
x = _________________
Answer: 30 degrees
The combined angle measure is 180°. The 180° angle measure is the sum of two parts. One angle is 150°.
Let x represent the unknown angle measure.
x + 150 = 180
x = 180 – 150 = 30 degrees
Question 6.
Find the value of r.
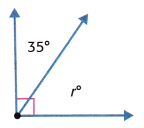
r = _________________
Answer: 55 degrees
The combined angle measure is 90°. The 90° angle measure is the sum of two parts. One angle is 35°.
Let r represent the unknown angle measure.
r + 35 = 90
r = 90 – 35 = 55 degrees
Problem Solving
Question 7.
Mathematical PRACTICE Make a Plan Suppose you draw a line from the center of a clock face to the number 12. When the minute hand gets to 3 on the clock face, the line and minute hand form a 90° angle. What angle does the line and the minute hand make when the minute hand is on 2?
Answer: 55 degrees
When hour and minute hand are at 12 and 2, then the time showing is 12:10
A clock is shaped like a circle and is composed of 360 degrees.
There are 60 minutes in an hour, and 360 degrees divided by 60 minutes is 6. Therefore, the minute hand moves 6 degrees per minute.
It takes 720 minutes for the hour hand to move around the clock. 360 degrees divided by 720 minutes is 0.5. Therefore, the hour hand moves 0.5 degrees per minute.
At 12:10, the hour hand has moved 10 out of 720 possible times from the top of the clock. 10 times 0.5 degrees is 5 degrees.
At 12:10, the minute hand has moved 10 out of 60 possible times from the top of the clock. 10 times 6 degrees is 60 degrees.
60-5 = 55 degrees
Test Practice
Question 8.
The combined angle measure is 120°. What is the value of n?
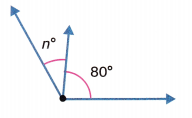
(A) 45
(B) 40
(C) 35
(D) 30
Answer: B (40)
The combined angle measure is 120°. The 120° angle measure is the sum of two parts. One angle is 80°.
Let k represent the unknown angle measure.
k + 80 = 120
k = 120 – 80 = 40 degrees