All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 14 Lesson 11 Problem-Solving Investigation: Make a Model will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Answer Key Chapter 14 Lesson 11 Problem-Solving Investigation: Make a Model
Learn the Strategy
Maya has a square piece of paper. She folds it in half so there are two triangle-shaped parts. She folds it in half again so there are four triangle-shaped parts. When she unfolds the paper, how many right angles are shown?

1. Understand
What facts do you kn0w?
Maya folds a piece of paper in half ___________ times diagonally.
What do you need to find?
the number of right angles when the paper is unfolded
2. Plan
I will make a model to find the answer.
3. Solve
Use a square piece of paper. Follow the same steps that Maya followed.
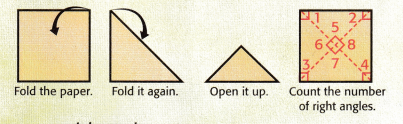
So, there are _____________ right angles.
4. Check
Does your answer make sense? Explain.
Answer:
1. Maya folds a piece of paper in half 2 times diagonally.
2. So, there are 8 right angles.
1. Understand
What facts do you know?
Maya folds a piece of paper in half 2 times diagonally.
What do you need to find?
the number of right angles when the paper is unfolded
2. Plan
I will make a model to find the answer.
3. Solve
Use a square piece of paper. Follow the same steps that Maya followed.
So, there are 8 right angles.
4. Check
Does your answer make sense? Explain.
Yes, the above answer makes sense, as we made and verified by folding the paper.
Practice the Strategy
Sam has a card that is a quadrilateral. All sides are equal length. One of the angles measures 60°. Which quadrilateral is Sam’s card?

1. Understand
What facts do you know?
What do you need to find?
2. Plan
3. Solve
4. Check
Does your answer make sense? Explain.
Answer: Rhombus
1. Understand
What facts do you know?
A quadrilateral where all sides are equal length and one of the angles measures 60°
What do you need to find?
Which quadrilateral is Sam was referring.
2. Plan
I will make a quadrilateral with the given requirements.
3. Solve
A Rhombus is a type of a quadrilateral where all the sides are of equal length and the opposite angles are measured to be equal. One of the angles measures 60° in it.
4. Check
Does your answer make sense? Explain.
Yes, the above answer makes sense, as we observed the same by illustrating the above as a figure.
Apply the Strategy
Solve each problem by making a model.
Question 1.
Mathematical PRACTICE Identify Structure Mary Anne is making a pattern with quadrilaterals. She put squares in the first row, parallelograms in the second row, and trapezoids in the third row. She repeats this pattern four times. Which quadrilateral does she use in the tenth row?
Answer: Squares
1. Understand
What facts do you know?
Mary Anne is making a patterns with quadrilaterals. She put squares in the first row, parallelograms in the second row, and trapezoids in the third row.
What do you need to find?
The quadrilateral she is using in the tenth row.
2. Plan
Draw the above patterns exactly as mentioned in the question on the paper and observe the required pattern
3. Solve
After drawing the patterns and observing the same, the quadrilateral she used in the tenth row is Squares
4. Check
Does your answer make sense? Explain.
Yes, the above answer makes sense, as we observed the same by illustrating the above as a figure.
Question 2.
Mathematical PRACTICE Model Math Draw two lines on the square below so that three right triangles are formed.
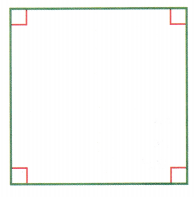
Answer:
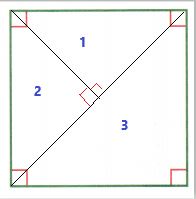
1. Understand
What facts do you know?
Given a square
What do you need to find?
Form three right angled triangles using two lines in a square.
2. Plan
Draw two lines on the square below so that three right triangles are formed.
3. Solve

As you can observe in the above figure, two lines are drawn in a square, which is in black color. these two lines divide the square into three right triangles, which was mentioned in the above figure.
4. Check
Does your answer make sense? Explain.
Yes, it makes sense as we observed above explanation and figure.
Question 3.
Mathematical PRACTICE Explain to a Friend The first time a pizza is cut in half, there are 2 pieces. The second time each piece is cut in half, there are 4 pieces. The third time each piece is cut in half, there are 8 pieces. How many pieces will there be after each piece is cut the fourth time? Explain how you solved the problem.

Answer: 16 pieces
1. Understand
What facts do you know?
The first time a pizza is cut in half, there are 2 pieces. The second time each piece is cut in half, there are 4 pieces. The third time each piece is cut in half, there are 8 pieces.
What do you need to find?
The number of pieces that will be there after each piece is cut the fourth time
2. Plan
Imagine each piece cutting into half and make a pattern
3. Solve
The first time a pizza is cut in half, there are 2 pieces. The second time each piece is cut in half, there are 4 pieces. The third time each piece is cut in half, there are 8 pieces. As you can observe the pattern, every time you are cutting the pieces into half, the pieces are multiplied by 2 each time than the previous one. So, for the fourth time, if you cut the pieces into half, they will get multiplied by 2 than the third time. Therefore, 16 pieces that will there be after each piece is cut the fourth time
4. Check
Does your answer make sense? Explain.
Yes, it makes sense as we observed above explanation.
Review the Strategies
- Use any strategy to solve each problem.
- Make a model.
- Find a pattern.
- Make a table.
- Guess, check, and revise.
Question 4.
Mathematical PRACTICE Look for a Pattern Mandy does one chore a day for her allowance. One day she washes dishes, the next she walks the dog, and the next she folds laundry. If she starts this cycle of chores on a Monday, which chore will she be doing the following Monday?
Answer: she walks the dog
1. Understand
What facts do you know?
Mandy does one chore a day for her allowance. One day she washes dishes, the next she walks the dog, and the next she folds laundry. she starts this cycle of chores on a Monday.
What do you need to find?
which chore will she be doing the following Monday?
2. Plan
Note down the above patterns exactly as mentioned in the question and observe the required pattern
3. Solve
After noting down the patterns and observing the same, she walks the dog on the following Monday.
4. Check
Does your answer make sense? Explain.
Yes, it makes sense as we observed above.
Question 5.
Kendra took photographs at the park. She photographed 20 dogs and owners in all. If there was a total of 64 legs, how many dogs and owners were there?
Answer: 8 owners and 12 dogs
1. Understand
What facts do you know?
Kendra photographed 20 dogs and owners in all. There was a total of 64 legs in the photograph.
What do you need to find?
Total number of dogs and owners in the photograph
2. Plan
Assume that every owner has 2 legs, each dog has 4 legs. Form an equation using the above information and solve them accordingly.
3. Solve
Assume that every owner has 2 legs, each dog has 4 legs.
Let X be the total number of owners and Y be the total number of dogs.
Then, X+ Y = 20 -> (1)
On the other hand the total number of legs is equal to 4 X + 2 Y = 64 -> (2)
We have to resolve this system of equations:
X+ Y = 20
4 X + 2 Y = 64
From the first equation: X=20-Y
Substituting to the second one we get: 4 X + 2 Y = 64
4(20-Y)+2Y = 64
80 – 4Y + 2Y = 64
-4Y + 2Y = 64 – 80
-2Y = -24
2Y = 24
Y=12,
hence X=20-12=8
Thus there were 8 owners and 12 dogs.
4. Check
Does your answer make sense? Explain.
Yes, it makes sense, as you can observe in the above explanation in step 3.
Question 6.
Mathematical PRACTICE Identify Structure Corey drew 8 shapes. Four are squares, two are triangles, and the rest are parallelograms. Write two fractions that name the part of the shapes that are quadrilaterals.
Answer: The fraction of squares = \(\frac{4}{8}\) and The fraction of parallelograms = \(\frac{2}{8}\).
1. Understand
What facts do you know?
Corey drew 8 shapes. Four are squares, two are triangles, and the rest are parallelograms. So, the number of parallelograms are 2 (8 -4- 2)
What do you need to find?
The two fractions that name the part of the shapes that are quadrilaterals. The quadrilateral shapes that are given in question are squares and parallelograms.
2. Plan
Identify the required quadrilaterals out of given shapes. Now, measure the fraction of the quadrilateral shapes.
3. Solve
Total number of shapes = 8
The quadrilateral shapes that are given in question are squares and parallelograms.
number of squares are 4
number of parallelograms are 2
The fraction of squares can be obtained by dividing number of squares by total shapes, which is \(\frac{4}{8}\).
The fraction of parallelograms can be obtained by dividing number of parallelograms by total shapes, which is \(\frac{2}{8}\).
4. Check
Does your answer make sense? Explain.
Yes, it makes sense, as you can observe in the above explanation in step 3.
Question 7.
Mathematical PRACTICE Make Sense of Problems Mr. Lawrence used 100 tiles when he put a new floor in the kitchen. Thirty-four tiles are squares and 16 tiles are rectangles. Write the total amount of tiles that are squares and rectangles as a decimal and a fraction.
Answer: \(\frac{50}{100}\) = \(\frac{1}{2}\) = 0.50
1. Understand
What facts do you know?
Mr. Lawrence used 100 tiles when he put a new floor in the kitchen. Thirty-four tiles are squares and 16 tiles are rectangles.
What do you need to find?
total amount of tiles that are squares and rectangles as a decimal and a fraction.
2. Plan
Find out the total number of squares and rectangles and measure its fraction out of total number of tiles.
3. Solve
number of squares = 34
number of rectangles = 16
total number of squares and rectangles = 34 + 16 = 50
Now divide 50 by total number of tiles 100, which is \(\frac{50}{100}\), by simplification it is \(\frac{1}{2}\).
\(\frac{50}{100}\) = 0.50 in decimal
4. Check
Does your answer make sense? Explain.
Yes, it makes sense, as you can observe in the above explanation in step 3.
McGraw Hill My Math Grade 4 Chapter 14 Lesson 11 My Homework Answer Key
Problem Solving
Solve each problem by making a model.
Question 1.
Mathematical PRACTICE Identify Structure A quadrilateral has sides that measure 12 centimeters, 10 centimeters, 10 centimeters, and 5 centimeters. The side that measures 12 centimeters is parallel to the side that measures 5 centimeters. What is the figure?
Answer: Trapezoid
1. Understand
What facts do you know?
A quadrilateral has sides that measure 12 centimeters, 10 centimeters, 10 centimeters, and 5 centimeters. The side that measures 12 centimeters is parallel to the side that measures 5 centimeters.
What do you need to find?
The figure formed using the above measurements.
2. Plan
Draw the figure using the above measurements.
3. Solve
Dimensions of a quadrilateral are 12 cm , 10 cm, 10 cm, and 5 cm. And the side that measures 12 cm is parallel to the side measures 5 cm. So, it has two parallel sides in which one side is longer than the other side and the other two sides are of equal length. So, it will form a trapezium or trapezoid.
4. Check
Does your answer make sense? Explain.
Yes, it makes sense as we can observe in the above explanation.
Question 2.
Mathematical PRACTICE Explain to a Friend Katerina draws a square. She wants to draw one line to divide the square into 2 triangles. Is it possible for her to divide the square into 2 obtuse triangles? Explain.
Answer: Its not possible to divide the square into two obtuse triangles
1. Understand
What facts do you know?
Katerina draws a square. She draws one line to divide the square into 2 triangles.
What do you need to find?
Check whether the square can be divided into two obtuse angle triangles.
2. Plan
Imagine a square that was divided into two triangles by cutting along with its diagonal.
3. Solve
Its not possible to divide the square into two obtuse triangles since each angle within the square is 90 so if you were to draw a line between two of the edges you can only get two right angle triangle.
4. Check
Does your answer make sense? Explain.
Yes, it makes sense as we can observe in the above explanation.
Question 3.
Is it possible for a quadrilateral to have only 2 right angles? If so, draw an example.
Answer: Yes, Trapezoid
1. Understand
What facts do you know?
A quadrilateral was given with only two right angles
What do you need to find?
Is it possible for a quadrilateral to have only 2 right angles
2. Plan
imagine and draw the required figure
3. Solve
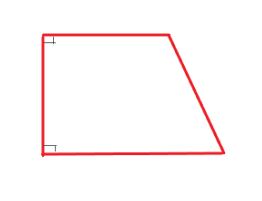
The trapezoid has two right angles. The above figure illustrated an trapezoid with two right angles where opposite sides are parallel to each other.
4. Check
Does your answer make sense? Explain.
Yes, it makes sense as you can observe in the above explanation and figure.
Question 4.
Mathematical PRACTICE Identify Structure Kirby drew a quadrilateral with four right angles, a side that measures 9 centimeters, and a side that measures 6 centimeters. What is the figure? What is its perimeter?
Answer: Rectangle with 30cms perimeter
1. Understand
What facts do you know?
a quadrilateral with four right angles, a side that measures 9 centimeters, and a side that measures 6 centimeters.
What do you need to find?
The figures that forms using the above dimensions and its perimeter.
2. Plan
3. Solve
Kirby drew a quadrilateral with 4 right angles, a side that measures 9 centimeters and a side that measure 6 centimeters.
Since quadrilateral has all its sides equal to 90 degrees and opposite sides are equal in size. Therefore, the quadrilateral is a rectangle.
Perimeter of the rectangle can be calculated using 2(l+b), where l is length of the rectangle and b is breath of the rectangle.
So, perimeter = 2(9+6) = 2(15) = 30 cms.
4. Check
Does your answer make sense? Explain.
Yes, it makes sense as you can observe in the above explanation.
Question 5.
Mathematical PRACTICE Be Precise Is it possible for a trapezoid to have only 3 right angles? Explain.
Answer: Not possible
1. Understand
What facts do you know?
The given assumed figure is trapezoid
What do you need to find?
Is it possible for a trapezoid to have only 3 right angles
2. Plan
Imagine a trapezoid and study its shape properties.
3. Solve
A trapezoid is a quadrilateral with only 1 pair of parallel sides. A quadrilateral has 360 degrees and 4 angles. As we need to assume 3 right angles and right angles are 90 degrees, the measure of the fourth angle is 360−3(90), or 90 degrees. Since the resultant figure has 4 right angles, its opposite sides must be parallel, so it cannot be a trapezoid.
4. Check
Does your answer make sense? Explain.
Yes, it makes sense as you can observe in the above explanation.