McGraw Hill My Math Grade 4 Chapter 13 Answer Key Perimeter and Area

All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 13 Perimeter and Area will give you a clear idea of the concepts.

McGraw-Hill My Math Grade 4 Answer Key Chapter 13 Perimeter and Area

Essential Question

Why is it important to measure perimeter and area?
Answer: The perimeter measures the outside distance of a shape. The area measures the inside space of a shape. The importance of measuring perimeter and area is for constructing a house, for painting purposes, for making crafts, etc.

Am I Ready

Draw an array to model each multiplication problem. Find the product.

Question 1.
4 × 8 = _____________
Answer: 32
Explanation:
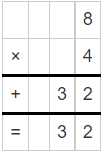
$McGraw-Hill My Math Grade 4 Answer Key Chapter 13 Perimeter and Area_1$
By multiplying 4 and 8 we get 32.

Question 2.
7 × 7 = _____________
Answer:49
Explanation:
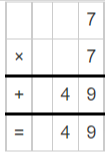
$McGraw-Hill My Math Grade 4 Answer Key Chapter 13 Perimeter and Area Problem 1$
By multiplying 7 and 7 we get the value is 49.

Question 3.
3 × 12 = _____________
Answer: 36
Explanation:
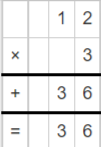
$McGraw-Hill My Math Grade 4 Answer Key Chapter 13 Perimeter and Area_3$
By multiplying 3 and 12, the value is 36.

Question 4.
10 × 4= _____________
Answer: 40
Explanation:
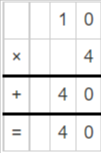
$McGraw-Hill My Math Grade 4 Answer Key Chapter 13 Perimeter and Area_4$
By multiplying 4 and 10, we get the value is 40.

Question 5.
9 × 11= _____________
Answer: 99
Explanation:
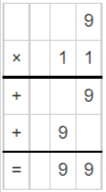
$McGraw-Hill My Math Grade 4 Answer Key Chapter 13 Perimeter and Area_5$
By multiplying 9 and 11, we get 99.

Question 6.
4 × 15 = _____________
Answer: 60
Explanation:
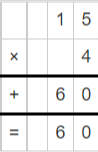
$McGraw-Hill My Math Grade 4 Answer Key Chapter 13 Perimeter and Area_6$
By multiplying 4 and 15, we get the value is 60.

Question 7.
Cora is making a picture. It will be a square. How many sides are the same length?
Answer: The square consists of four sides. All four sides are the same length.

My Math Words

Review Vocabulary
length
product

Making Connections
Use the review vocabulary to complete the chart.

Look at the array below. Write a multiplication problem to describe it. Then find the product.
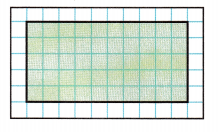
$McGraw Hill My Math Grade 4 Chapter 13 Answer Key Perimeter and Area 1$
Answer: 50
Explanation:
The shaded array consists of 10 rows and 5 columns.
So, the multiplication of 10 x 5 is 50.
By multiplying 5 and 10, we get the value is 50.

What number represents the length of this array?
$McGraw Hill My Math Grade 4 Chapter 13 Answer Key Perimeter and Area 2$
Answer: The column number represents the length of the array. The number is 8

Draw an array that represents a product of 20.
Answer: The product of 20 is 4 x 5.
$McGraw-Hill My Math Grade 4 Answer Key Chapter 13 Perimeter and Area_Image$
By multiplying 4 and 5, we get the product value is 20.

Suppose the array below represents a figure. Describe this figure’s sides.
$McGraw Hill My Math Grade 4 Chapter 13 Answer Key Perimeter and Area 3$
Answer: The figure looks like a rectangle. Rectangle opposite sides are equal in length.

My Vocabulary Cards

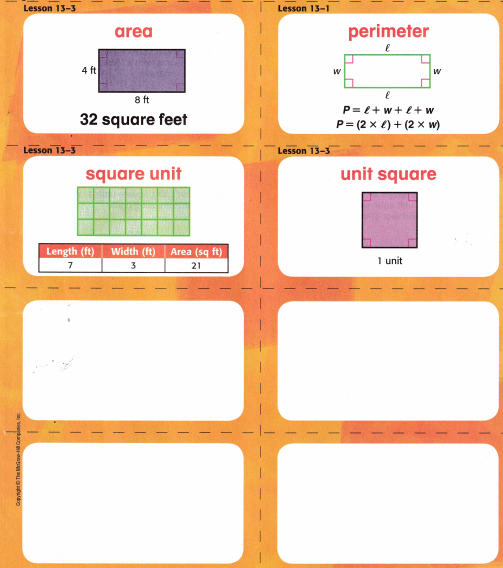
$McGraw Hill My Math Grade 4 Chapter 13 Answer Key Perimeter and Area 4$

Ideas for Use

Write a tally mark on each card every time you read or write the word. Challenge yourself to use at least 3 tally marks for each card.
Use the blank cards to review problem-solving strategies, such as working backward, making a table, or drawing a picture.

The distance around a dosed figure.
Would it be possible to double the lengths and sides of any figure to find its perimeter? Explain.
Answer: Yes, it is possible. For finding perimeter,
The formula is Perimeter = 2(L+B)

The number of square units needed to cover a figure without any overlap.
Draw a rectangle. Label the sides’ lengths. Exchange papers with a friend to find the area of the rectangle.
Answer: The area of the rectangle is 21.
Explanation:
$McGraw-Hill-My-Math-Grade-4-Answer-Key-Chapter-13-Perimeter-and-Area_Rectangle.png$
The area of the Rectangle is Length x width.
A = 7 x 3 = 21.

A square with a side length of one unit.
A friend tells you he used grid paper to draw a rectangle with a length of 12 unit squares and a width of 5 unit squares. What is the rectangle’s total number of unit squares?
Answer: The rectangle’s total number of unit squares is 12 x 5 is 60.

A unit for measuring area. Contains one unit square.
Explain how using square units to measure is different from using units.
Answer: Square units are used to measure the area.

My Foldable

Follow the steps on the back to make your Foldable.
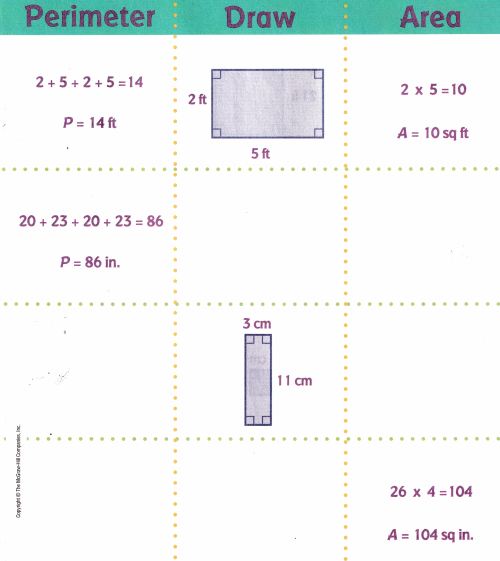
$McGraw Hill My Math Grade 4 Chapter 13 Answer Key Perimeter and Area 5$
$McGraw Hill My Math Grade 4 Chapter 13 Answer Key Perimeter and Area 6$
Answer:
(i) Given the Perimeter value, we will draw a figure and find the area.
The figure is,
$McGraw-Hill My Math Grade 4 Answer Key Chapter 13 Perimeter and Area_$
The area of a Rectangle is, L x B
= 20 x 23
= 460 sq.inches.

(ii) Given the rectangle, find the perimeter and Area.
Perimeter = 2(l+b)
= 2(3+11)
=2(14) = 28 cm
Now, the Area of a Rectangle is l x b.
= 3 x 11
A = 33 sq.cm.

(iii) Given the Area, draw the figure and find the perimeter.
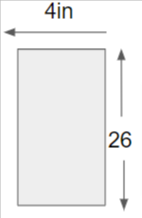
$McGraw-Hill My Math Grade 4 Answer Key Chapter 13 Perimeter and Area_(iii)$
The perimeter is 2(l+b)
= 2(4+26)
= 2(30)
P = 60 inches.

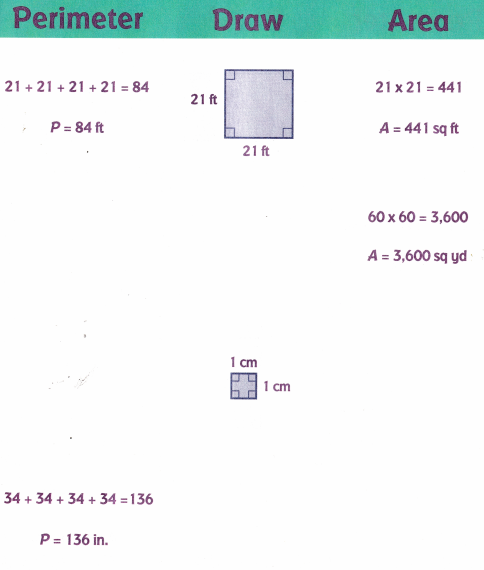
(iv) Given the square Area, draw the figure and find the perimeter.
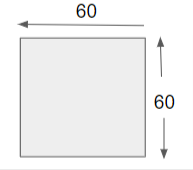
$McGraw-Hill My Math Grade 4 Answer Key Chapter 13 Perimeter and Area_(iv)$
The perimeter of a square is 4a
= 4*60
P = 240 yd.

(v) Given the square, find the perimeter and Area.
Perimeter = 4a
= 4(1)
=4 cm
Now, the Area of a square is,
= 4 x 4
A = 16 sq.cm.

(vi) Given the Perimeter value, we will draw a figure and find the area.
The figure is,
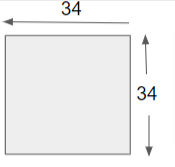
$McGraw-Hill My Math Grade 4 Answer Key Chapter 13 Perimeter and Area_(vi)$
The Area of a square is, a x a
A = 34 x 34
A = 1156 sq.in

McGraw-Hill My Math Grade 4 Answer Key Chapter 13 Perimeter and Area

Leave a Comment Cancel Reply