All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 11 Lesson 9 Solve Measurement Problems will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Answer Key Chapter 11 Lesson 9 Solve Measurement Problems
Math in My World
Example 1
The blue trail at the park is \(\frac{3}{4}\) mile long. The red trail is 1\(\frac{1}{4}\) miles long. Stella wants to hike both trails. How many feet will she hike in all?

1. Find the total number of miles.
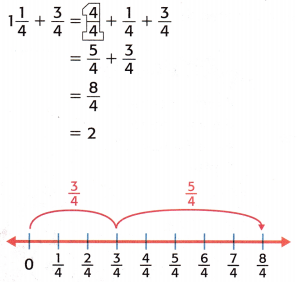
Stella will hike 2 miles.
2. Convert the miles to feet.
1 mile = 5,280 feet
Multiply 2 miles by 5,280 to find the total number of feet. 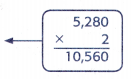
So, Stella will hike ______________ feet in all.
Answer:
So, Stella will hike 10,560 feet in all.
Example 2
Dominic weighed an apple and a watermelon. The apple weighed 5 ounces. The watermelon weighed 20 pounds. How many more ounces did the watermelon weigh than the apple?

1. Find the total number of ounces the watermelon weighed.
There are 16 ounces in a pound.
Multiply 20 by 16.
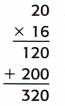
The watermelon weighed 320 ounces.
2. Find the difference in ounces.
320 oz – 5 oz = ______________ oz
So, the watermelon weighed ______________ ounces more than the apple.
Answer:
320 oz – 5 oz = 315 oz
So, the watermelon weighed 315 ounces more than the apple.
Talk Math
Which operations did you use to solve Exercise 2? Explain.

Answer:
To convert larger units to smaller units, we used multiplication operation.
To find the difference, we used subtraction operation.
Guided Practice
Question 1.
Stan has 4 pints of milk. Gianna has twice as much milk as Stan. How many fluid ounces of milk does Gianna have?
4 pints × 2 = ______________ pints
Gianna has ______________ pints of milk.
8 pints × 16 = ______________ fluid ounces
Gianna has ______________ fluid ounces of milk.
Answer:
4 pints × 2 = 8 pints
Gianna has 8 pints of milk.
8 pints × 16 = 128 fluid ounces
Gianna has 128 fluid ounces of milk.
Question 2.
Molly went to her grandma’s house for 16 hours last weekend. This was four times longer than the time she spent at her grandma’s this weekend. How many minutes was Molly at her grandma’s house this weekend?
Answer:
Given that: Molly went to her grandma’s house for 16 hours last weekend. This was four times longer than the time she spent at her grandma’s this weekend.
As this is 4 times longer than the time she spent at her grandma’s this weekend.We need to divide the last weekend’s time by 4.
16÷4=4 hrs
1 hour equals 60 mins.
4 × 60 mins = 240 mins.
240 minutes were spend by Molly at her grandma’s house this weekend.
Independent Practice
Question 3.
Jayden read to his little sister for 10 minutes on Saturday and 12 minutes on Sunday. How many seconds did he read to her on Saturday and Sunday? Circle what to do to solve this problem.
- Add 10 and 12 and then multiply by 60.
- Add 10 and 12 and then multiply by 30.
- Add 10 and 12 and then divide by 60.
- Add 10 and 12 and then subtract 60.
Solve.
Jayden read to his little sister for ________________.
Answer:
Given that: Jayden read to his little sister for 10 minutes on Saturday and 12 minutes on Sunday.
First we need to add the minutes read on Saturday and Sunday.
Total minutes will be 10+12=22 mins.
Since 1 min is 60 secs, multiply 22 by 60.
22 × 60 = 1320 secs
Therefore to solve this problem, first we need to add 10+12 and then multiply by 60.
Question 4.
Mackenzie’s dog can jump 2\(\frac{1}{2}\) feet off the ground. Jordyn’s dog can jump \(\frac{1}{2}\) foot off the ground. What is the difference in inches between how high Mackenzie’s dog can jump and how high Jordyn’s dog can jump? Circle what to do to solve this problem.
- Subtract 2\(\frac{1}{2}\) ft – \(\frac{1}{2}\) ft and then multiply by 3.
- Subtract 2\(\frac{1}{2}\) ft – \(\frac{1}{2}\) ft and then divide by 3.
- Subtract 2\(\frac{1}{2}\) ft – \(\frac{1}{2}\) ft and then multiply by 12.
- Add 2\(\frac{1}{2}\) ft – \(\frac{1}{2}\) ft and then multiply by 12.
Use the number line to help solve.
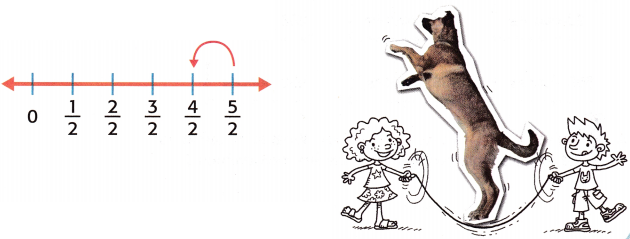
The difference in inches is _______________.
Answer:
Given that: Mackenzie’s dog can jump 2\(\frac{1}{2}\) feet off the ground. Jordyn’s dog can jump \(\frac{1}{2}\) foot off the ground.
To find the difference, we need to subtract 2\(\frac{1}{2}\) – \(\frac{1}{2}\) = ((2 × \(\frac{2}{2}\)) + \(\frac{1}{2}\)) – \(\frac{1}{2}\)
\(\frac{5}{2}\) – \(\frac{1}{2}\)
\(\frac{4}{2}\) feet.
1 feet equal 12 inches.
\(\frac{4}{2}\) or 2 feet will be 24 in.
Therefore to solve this problem, we need to subtract 2\(\frac{1}{2}\) ft – \(\frac{1}{2}\) ft and then multiply by 12.
Problem Solving
Question 5.
Brooklyn bought 1 pound of cucumbers for a salad. She bought twice as much lettuce. How many ounces of lettuce did Brooklyn buy for the salad?

Answer:
Given that: Brooklyn bought 1 pound of cucumbers for a salad. She bought twice as much lettuce.
So, she bought 2 pounds of lettuce.
1 pound equals 16 ounce.
2 pounds will be equal to 2×16 = 32 ounces.
She bought 32 ounces of lettuce for the salad.
Question 6.
Mathematical PRACTICE Use Math Tools Sebastian needs 2 gallons of juice for his party. How many cups of juice is this?
Answer:
Given that: Sebastian needs 2 gallons of juice for his party.
Since 1 gallon equals to 16 cups, multiply by 2.
2×16 = 32 cups.
This is 32 cups of juice.
Question 7.
The practice field is 13 yards long. How many feet is this?
Answer:
Since 1 yard equals to 3 feet, multiply by 3.
13×3 = 39 feet.
The practice field is 39 feet long.
Question 8.
Jacob needs \(\frac{1}{2}\) pint of milk for his recipe. He needs \(\frac{1}{2}\) pint of water. How many cups will he have after he combines both ingredients?
Answer:
Given that: Jacob needs \(\frac{1}{2}\) pint of milk for his recipe. He needs \(\frac{1}{2}\) pint of water.
Combining both ingredients, \(\frac{1}{2}\)+\(\frac{1}{2}\) = \(\frac{2}{2}\) or 1 pint.
1 pint equals to 2 cups.
It will be 2 cups after he combines both ingredients.
HOT Problems
Question 9.
Mathematical PRACTICE Use Number Sense The moving company charges extra money to move boxes weighing more than 25 pounds. Circle the packages that weigh less than 25 pounds. Put an X on the packages that weigh more than 25 pounds.

Answer:
1 pound equals 16 ounces.
25 pounds will be 25×16= 400 ounces.
We need to circle the packages that weigh less than 25 pounds or 400 ounces, which are 320 ounces, 288 ounces, 368 ounces and 352 ounces.
Above 25 pounds packages, we need to put X mark, so they will be 480 ounces and 432 ounces.

Question 10.
Building on the Essential Question What information do I need to solve word problems that involve measurement?
Answer:
The relationship between the two provided numbers is necessary.
The measurement units for the given numbers are required.
If metric conversion is required, the information for the conversion unit is also required.
McGraw Hill My Math Grade 4 Chapter 11 Lesson 9 My Homework Answer Key
Practice
For Exercises 1-3, use the following information.
Marissa bought 2\(\frac{1}{2}\) gallons of orange juice to make punch.
Question 1.
How many quarts of orange juice did Marissa buy?
Answer:
1 gallon equals 4 quarts.
2 gallons will be 2×4=8 quarts.
\(\frac{1}{2}\) of gallon equals 2 quarts.
8+2=10 quarts
So, Marissa should buy 10 quarts of orange juice.
Question 2.
Marissa bought 6 fewer pints of soda than of orange juice. How many cups of soda did she buy?
Answer:
She bought 10 quarts of orange juice.
Since, 1 quart equals to 2 pints, multiply by 2.
2×10=20 pints.
She bought 6 fewer pints of soda than of orange juice. Therefore, she bought 20-6=14 pints of orange juice.
Question 3.
Marissa pours 1\(\frac{1}{2}\) cups of punch in each glass. How many fluid ounces is each serving?
Answer:
She pours 1\(\frac{1}{2}\) cups of punch in each glass.
Since 1 cup equals to 8 fluid ounces, multiply by 8.
1 cup equals to 8 fluid ounces.
\(\frac{1}{2}\) cup will be equal to 4 fluid ounces.
8+4=12 fluid ounces.
There will be 12 fluid ounces in each serving.
Problem Solving
For Exercises 4-6, use the following information.
Martin sorted the bolts in his toolbox by size. They measured \(\frac{3}{8}\) inch, \(\frac{1}{2}\) inch, \(\frac{5}{8}\) inch, \(\frac{7}{8}\) inch, and 1\(\frac{1}{4}\) inches.
Question 4.
What is the difference in length between the longest bolt and the shortest bolt?
Answer:
Given lengths are \(\frac{3}{8}\) inch, \(\frac{1}{2}\) inch, \(\frac{5}{8}\) inch, \(\frac{7}{8}\) inch, and 1\(\frac{1}{4}\) inches.
First we need to convert them to like fractions.
\(\frac{1}{2}\) ×\(\frac{4}{4}\) = \(\frac{4}{8}\)
1\(\frac{1}{4}\) will be (1×\(\frac{8}{8}\))+(2×\(\frac{1}{4}\))
\(\frac{8}{8}\)+\(\frac{2}{8}\) = \(\frac{10}{8}\)
Now the lengths are \(\frac{3}{8}\) inch, \(\frac{4}{8}\) inch, \(\frac{5}{8}\) inch, \(\frac{7}{8}\) inch, and \(\frac{10}{8}\) inches.
The length of longest bolt is = \(\frac{10}{8}\) inches
The length of shortest bolt is = \(\frac{3}{8}\) inch
The difference of length between the longest bolt and the shortest bolt will be \(\frac{10}{8}\) – \(\frac{3}{8}\) = \(\frac{7}{8}\) inches.
Question 5.
If you laid one of each size bolt end-to-end, how long would the row of bolts be?
Answer:
\(\frac{3}{8}\) + \(\frac{4}{8}\) + \(\frac{5}{8}\) + \(\frac{7}{8}\) + \(\frac{10}{8}\) = \(\frac{29}{8}\)
If one of each size bolt are laid end-to-end, the row of bolts would be \(\frac{29}{8}\) inches long.
Question 6.
If you laid 9 bolts end-to-end that each measure \(\frac{7}{8}\) inch, how long would the row of bolts be?
Answer:
If we lay 9 bolts of \(\frac{7}{8}\) inch end to end, the total length would be 9 times \(\frac{7}{8}\) inches.
9× \(\frac{7}{8}\) = \(\frac{63}{8}\) inch
Question 7.
Aurora is moving to a new house. She has lived in her current house for 6 years. How many months is that? How many days?
Answer:
Given that: Aurora is moving to a new house. She has lived in her current house for 6 years.
Since 1 year equals to 12 months, multiply by 12.
6 years will be 6×12=72 months.
1 year equals to 365 days.so, 6 years will be 6×365=2190 days.
She has lived in her current house for 6 years or 72 months or 2190 days.
Question 8.
Mathematical PRACTICE if Use Math Tools Nolan bought 26 yards of heavy-duty rope at the hardware store The rope costs $2 per foot. How much did Nolan pay for the rope?
Answer:
Given that: Nolan bought 26 yards of heavy-duty rope at the hardware store The rope costs $2 per foot.
1 yard equals 3 foot.
26 yards will be 78 foot.
The rope costs $2 per foot.So for 76 foot it should be 76×2 = 152.
Nolan should pay $152 for 78 foot of rope.
Test Practice
Question 9.
Kim and her two brothers each use 1\(\frac{1}{2}\) cups of milk for breakfast. How many fluid ounces of milk do they use in 4 days?
(A) 144 fl oz
(B) 108 fl oz
(C) 72 fl oz
(D) 36 fl oz
Answer:
1 cup equals to 8 fl oz.
\(\frac{1}{2}\) cup equals to 4 fl oz.
Total milk used will be 12 fl oz.
Kim and her two brothers each uses 12 fl oz of milk for breakfast.
For 4 days, each will be using 12×4=48 fl oz.
Total milk three members would have used will be 48×3=144 fl oz.
Therefore, option A is correct.