All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 10 Fractions and Decimals will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Answer Key Chapter 10 Fractions and Decimals
Essential Question
How are fractions and decimals related?
Answer: Noninteger, or partial, numbers can be expressed using both fractions and decimals. The ratio between two numbers is a fraction. Often, these numbers are each whole numbers, represented in \(\frac{p}{q}\) form such as \(\frac{1}{2}\) or \(\frac{7}{10}\). Decimals are defined as the digits that come after the decimal point and are numbers that fall between integers. The spaces past the decimal point are known as tenths, hundredths, thousandths and so on because decimals use a system of numbers based on units of tens.
Additionally, fractions can be expressed as decimals by performing the division of the ratio. (For example, \(\frac{1}{4}\) is equivalent to 1 divided by 4, or 0.25.) Decimals can also be expressed as fractions in terms of tenths, hundredths, thousandths and so on. (For example, 0.25 is equivalent to 25 hundrendths, which is equivalent to \(\frac{25}{100}\).)
Am I Ready
Write a fraction to describe the part that is green.
Question 1.

Answer: \(\frac{7}{10}\)
There are 10 parts in total, 7 of which are green.
So, Numerator indicates green color parts and Denominator indicates Total parts.
Thus, Green color parts (Numerator) / Total parts (Denominator) = \(\frac{7}{10}\).
Question 2.

Answer: \(\frac{2}{10}\)
There are 10 parts in total, 2 of which are green.
So, Numerator indicates green color parts and Denominator indicates Total parts.
Thus, Green color parts (Numerator) / Total parts (Denominator) = \(\frac{2}{10}\).
Question 3.

Answer: \(\frac{68}{100}\)
There are 100 parts in total, 68 of which are green.
So, Numerator indicates green color parts and Denominator indicates Total parts.
Thus, Green color parts (Numerator) / Total parts (Denominator) = \(\frac{68}{100}\).
Write each as a fraction.
Question 4.
four tenths
Answer: \(\frac{4}{10}\)
4 tenths as a fraction is \(\frac{4}{10}\)since it is 4 over ten.
Question 5.
eight tenths
Answer: \(\frac{8}{10}\)
8 tenths as a fraction is \(\frac{8}{10}\) since it is 8 over ten.
Question 6.
twenty hundredths
Answer: \(\frac{20}{100}\)
20 Hundredths as a fraction is \(\frac{20}{100}\) since it is 20 over hundred.
Question 7.
On Tuesday, seven tenths of an inch of rain fell. Write the amount of rain as a fraction.
Answer: \(\frac{7}{10}\)
Here, the total number of parts is 10.
We have to take only 7 equal parts out of 10 equal part
Thus, the required fraction =\(\frac{7}{10}\)
Algebra Find each unknown.
Question 8.
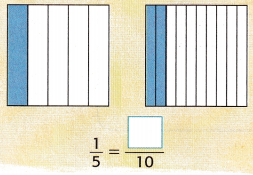
Answer: \(\frac{2}{10}\)
\(\frac{1}{5}\) is indicated as blue colored parts in total parts.
Similarly, there are 10 parts in total, 2 of which are in blue.
This shows that the parts in left hand side are doubled in right hand side. Hence the fraction got doubled.
Question 9.
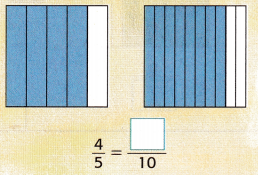
Answer: \(\frac{8}{10}\)
\(\frac{4}{5}\) is indicated as blue colored parts in total parts.
Similarly, there are 10 parts in total, 8 of which are in blue.
This shows that the parts in left hand side are doubled in right hand side. Hence the fraction got doubled.
My Math Words
Review Vocabulary
equivalent
fraction
place value
Making Connections
Use the review vocabulary to make equivalent fractions. Find the unknown in the fraction or shade to complete the area model.
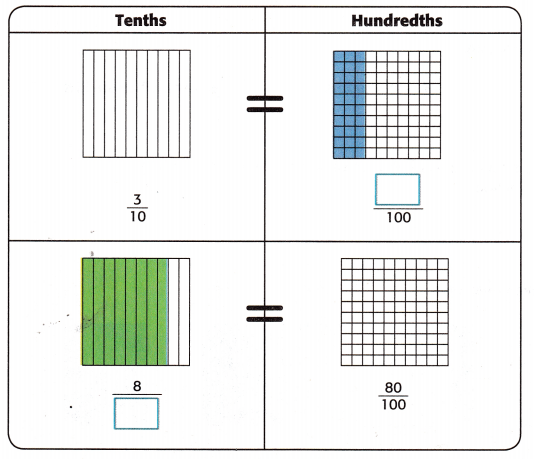
Answer: i) \(\frac{3}{10}\) equivalent fraction is \(\frac{30}{100}\)
There are 100 parts in total, 30 of which are in blue color.
ii) \(\frac{80}{100}\) equivalent fraction is \(\frac{8}{10}\)
There are 10 parts in total, 8 of which are in green color.
To determine equivalent fractions, divide the fraction’s numerator and denominator by the same number (common factor).
Although \(\frac{3}{10}\) may look like a different fraction, it is actually equivalent to {\(\frac{30}{100}\)} [\(\frac{3}{10}\)divided by \(\frac{10}{10}\) = \(\frac{30}{100}\)]
Similarly, \(\frac{80}{100}\)may look like a different fraction, it is actually equivalent to {\(\frac{8}{10}\)} [(\(\frac{80}{100}\) divided by \(\frac{10}{10}\) = \(\frac{8}{10}\)]
My Vocabulary Cards
Ideas for Use
- Draw or write examples for each card. Be sure your examples are different from what is shown on each card.
- Use a blank card to write a word from a previous chapter that you would like to review.
- Use a blank card to write this chapter’s essential question. Use the back of the card to write or draw examples that help you answer the question.
One of one hundred equal parts.
Write thirty-one hundredths as a decimal.
Answer: 0.31
If you divide 31 by one hundred you get 31 hundredths as a decimal which is 0.31
A number that uses place value and a decimal point to show part of a whole.
Explain how decimals and fractions are alike.
Answer: Noninteger, or partial, numbers can be expressed using both fractions and decimals. The ratio between two numbers is a fraction. Often, these numbers are each whole numbers, represented in \(\frac{p}{q}\) form such as \(\frac{1}{2}\) or \(\frac{7}{10}\). Decimals are defined as the digits that come after the decimal point and are numbers that fall between integers. The spaces past the decimal point are known as tenths, hundredths, thousandths and so on because decimals use a system of numbers based on units of tens.
Additionally, fractions can be expressed as decimals by performing the division of the ratio. (For example, \(\frac{1}{4}\) is equivalent to 1 divided by 4, or 0.25.) Decimals can also be expressed as fractions in terms of tenths, hundredths, thousandths and so on. (For example, 0.25 is equivalent to 25 hundrendths, which is equivalent to \(\frac{25}{100}\).)
One of ten equal parts.
Write six tenths as a decimal.
Answer: 0.6
six tenths is 6 divided by 10 and is written as 0.6.
Thus, the decimal part here indicated six tenths.
My Foldable
Follow the steps on the back to make your Foldable.
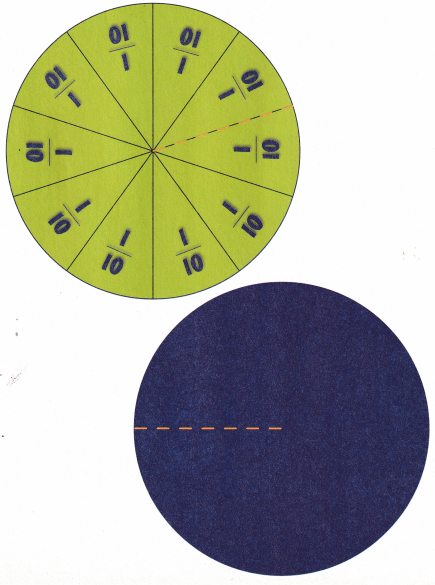
Answer: 3 (\(\frac{1}{10}\)) = \(\frac{3}{10}\)
In green color circle, there are total 10 parts where each part thus becomes \(\frac{1}{10}\)th part of total.
In step 3, blue color circle folds green color circle in such a way that only 3 parts are visible out of 10 parts.
Therefore, \(\frac{3}{10}\) is the required fraction from the folding.