All the solutions provided in McGraw Hill My Math Grade 3 Answer Key PDF Chapter 9 Properties and Equations will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 3 Answer Key Chapter 9 Properties and Equations
Essential Question
How are properties and equations used to group numbers?
Answer: The associative property gets its name from the word “Associate” and it refers to the grouping of numbers. This property states that when three or more numbers are added (or multiplied), the sum(or product) is the same regardless of the grouping of the addends (or multiplicands).
The most commonly used grouping symbols are parentheses. Operations inside parentheses can be done before any other operations in order to simplify the problem. for example 4(3 + 5).
Explanation:
The example for Associative property
The property which states that the grouping of the addends does not change the sum is called Associative property.
19 + (61 + 15) = 95
Associative property is used.
Hence, properties and equations used to group numbers
Am I Ready
Algebra Find each unknown.
Question 1.
8 + ![]() = 11
= 11
The unknown is _____________.
Answer: The unknown is 3
Explanation:
Given, 8 + ![]() = 11
= 11
Let the unknown be y
8 + y = 11
y = 11 – 8
y = 3 ,
To check, replace y value in the given equation, then we get
8 + 3 = 11
11 = 11
So, The Unknown is 3.
Question 2.
![]() × 5 = 20
× 5 = 20
The unknown is _____________.
Answer: The Unknown is 4.
Explanation:
Given, ![]() × 5 = 20
× 5 = 20
Let the unknown be y
5y = 20
y = \(\frac{20}{5}\)
y = 4 ,
To check, replace y value in the given equation, then we get
4 × 5 = 20
20 = 20
So, The Unknown is 4.
Question 3.
36 ÷ 6 = ![]()
The unknown is _____________.
Answer: The unknown is 6
Explanation:
Given, 36 ÷ 6 = ![]()
Let the unknown be y
36 ÷ 6 = y
y = \(\frac{36}{6}\)
y = 6 ,
So, The Unknown is 6.
Question 4.

The unknown is _____________.
Answer: The unknown is 9
Explanation:
Let the unknown be y
15 – y = 6
y = 15 – 6
y = 9.
So, The unknown is 9
Question 5.
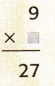
The unknown is _____________.
Answer: The unknown is 3
Explanation:
Let the unknown be y
9y = 27
y = \(\frac{27}{9}\)
y = 3.
So, The unknown is 3.
Question 6.
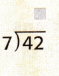
The unknown is _____________.
Answer: The unknown is 6.
Explanation:
Let the unknown be y
42 ÷ 7 = y
y = \(\frac{42}{7}\)
y = 6.
So, The unknown is 6.
Question 7.
Use the number sentence 12 + 15 + ![]() = 36 to find how many books Tony read in August.
= 36 to find how many books Tony read in August.

The unknown is ______________ books.
Answer: The unknown is 9 books
Explanation:
Given, 12 + 15 + y = 36
let the unknown be y
27 + y = 36
y = 36 – 27
y = 9
So, The unknown is 9 books.
Question 8.
Circle the property which is represented by 6 + 5 = 5 + 6.
Associative Property of Addition
Commutative Property of Addition
Identity Property of Addition
Answer: Commutative Property of Addition
Explanation:
Given, 6 + 5 = 5 + 6.
The commutative property states that the change in the order of two numbers in an addition or multiplication operation does not change the sum or the product.
So, 6 + 5 = 5 + 6 represents Commutative Property of Addition
Question 9.
Abia sold 1 more candle than Mel. Together, they sold 15 candles. Draw a picture that shows how many candles they each sold.
Answer: Mel sold 7 candles and Abia sold 8 candles ,Together, they sold 15 candles.
Explanation:
Given, Abia sold 1 more candle than Mel. Together, they sold 15 candles.
It will be, Mel sold 7 candles and Abia sold 8 candles , 7 + 8 = 15

So, Together, they sold 15 candles.
Question 10.
Daniela spent $20 at the grocery store and $15 at the gas station. How much did she spend in all? Write a number sentence with a symbol for the unknown. Solve.
Answer: She spent $35 in all.
Explanation:
Given, Daniela spent $20 at the grocery store and $15 at the gas station.
Let the unknown be y
$20 + $15 = y
y = $35
so, She spent $35 in all.
My Math Words
Review Vocabulary
array
decompose
equals sign (=)
known fact
unknown
Making Connections
Label each section of the flow chart with the correct review vocabulary word.
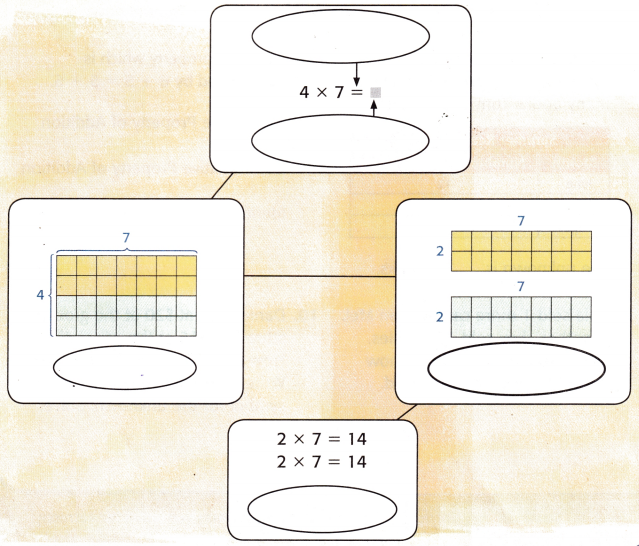
Answer: 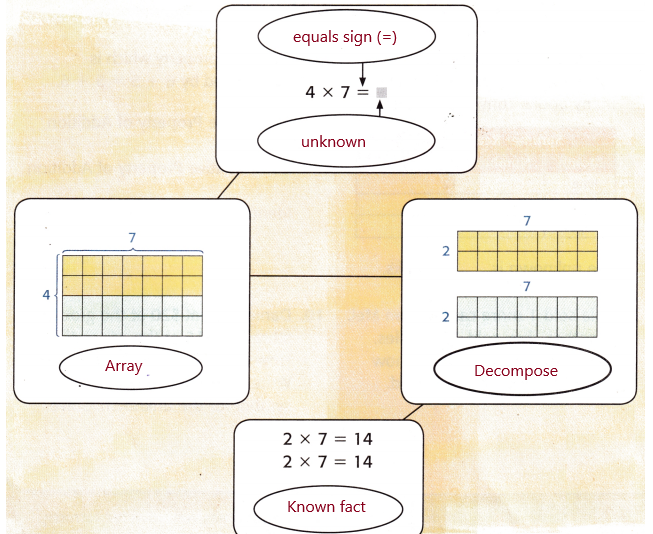
My Vocabulary Cards
Ideas for Use
- During this school year, create a separate stack of cards for key math verbs, such as evaluate. These verbs will help you in your problem solving.
- Use the blank card to write examples that will help you with concepts like writing and evaluating expressions.
This property allows you to decompose one factor into addends that are easier to multiply.
How can you use this method to find 7 × 2?
Answer: Distributive property allows you to decompose one factor into addends that are easier to multiply.
Explanation:
Given, 7 × 2 = 14
By using Distributive property, we get
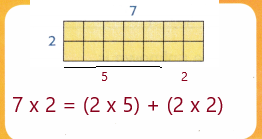
7 × 2 = 10 + 4
14 = 14.
So, Distributive property allows you to decompose one factor into addends that are easier to multiply.
To find the value of an expression.
How do parentheses help you evaluate the problem on the front of the card?
Answer: By solving inside the parentheses first, in order to find the value of an expression.
Explanation:
For example,
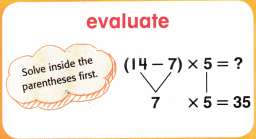
So, Always solve inside the parentheses first.
A mathematical process, which includes addition, subtraction, multiplication, and division.
Explain in your own words what it means to multiply.
Answer: multiply means the repeated addition of groups of equal sizes. Multiplication is one of the four basic arithmetic operations, alongside addition, subtraction, and division.
Explanation:

The property that states that the grouping of factors does not change the product. It can make multiplying 3 numbers easier.
Write a number sentence that is an example of the Associative Property of Multiplication.
Answer: The associative property gets its name from the word “Associate” and it refers to the grouping of numbers. This property states that when three or more numbers are added (or multiplied), the sum(or product) is the same regardless of the grouping of the addends (or multiplicands).
Explanation:

For example,
7 ×(2 × 3) = (7 × 2) × 3 = 42.
A sentence that contains an equals sign (=), showing that two expressions are equal.
How does knowing the meaning of equal help you remember the definition of equation?
Answer: the equal sign in mathematics describes equality between the values, equations, or expressions written on both sides.
Explanation:
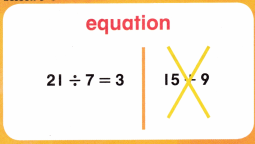
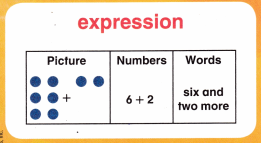
A combination of numbers and operations that represent a quantity.
How can the meaning of the word “express” help you remember what an expression is?
Answer: An expression in math is a sentence with a minimum of two numbers or variables and at least one math operation. This math operation can be addition, subtraction, multiplication, or division. The structure of an expression is: Expression is (Number/variable, Math Operator, Number/variable)
Explanation:
A letter or symbol, such as ![]() , ?, or m used to represent an unknown quantity.
, ?, or m used to represent an unknown quantity.
Variable is a multiple-meaning word. Use a dictionary to write the meaning of variable used in this sentence. The weather during spring can be variable.
Answer: The sentence meaning of ” The weather during spring can be variable”. is the weather is able to change in the spring.
Explanation:

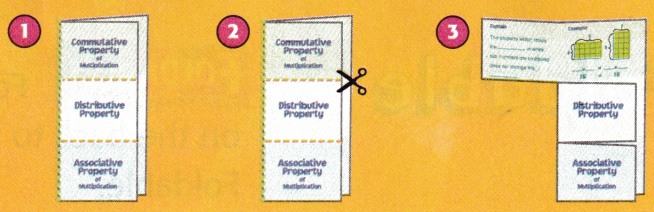
My Foldable
Follow the steps on the back to make your Foldable.

Explain
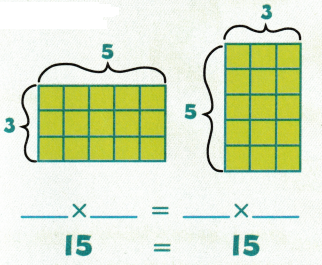
The property which states the ____________ in which two numbers are multiplied does not change the _____________.
Example
Answer: The property which states the order in which two numbers are multiplied does not change the product is commutative property
Explanation:
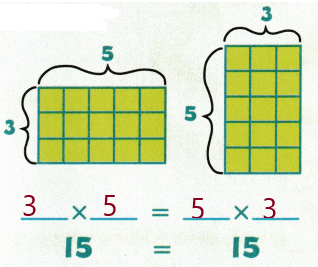
Given , 5 × 3 = 3 × 5
15 = 15.
So, The commutative property states that the change in the order of two numbers in an addition or multiplication operation does not change the sum or the product.
Explain
The property which allows me to _____________ factors into addends that are easier to work with.
Example
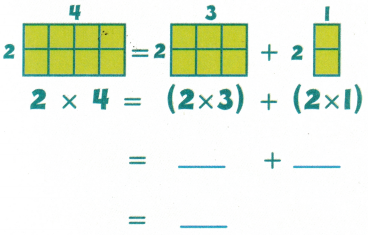
Answer: The property which allows me to decompose factors into addends that are easier to work with is Distributive property
Explanation:
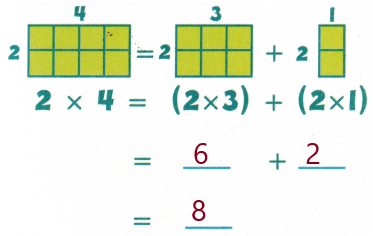
Given, 2 × 4 = ( 2 × 3 ) + ( 2 × 1)
8 = 6 + 2
8 = 8
So, Distributive property allows you to decompose one factor into addends that are easier to multiply.
Explain
The property which states that the grouping of _____________ does not change the ______________.
Example
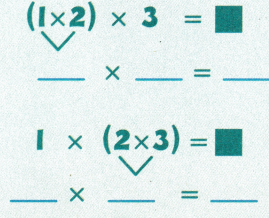
Answer: The property which states that the grouping of numbers does not change the product is Associative property.
Explanation:
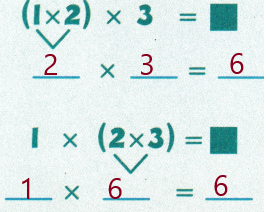
Given, (1 × 2) × 3 = 1 × ( 2 × 3 )
6 = 6
So, The associative property gets its name from the word “Associate” and it refers to the grouping of numbers.