All the solutions provided in McGraw Hill Math Grade 3 Answer Key PDF Chapter 5 Lesson 1 Model Division will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 3 Answer Key Chapter 5 Lesson 1 Model Division
Build It
Find how many in each group. Divide 12 counters into 3 equal groups. How many are in each group?
1. Partition one counter at a time into a group until all of the counters are gone.
Answer:
12 ÷ 3 = 4 in each group.
Explanation:
Given,
No of the counters are 12
Those are divided into 3 equal groups.
12 ÷ 3 = 4 in each group.
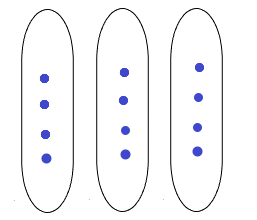
2. Draw the groups of counters.
Answer:
No of the counters given is 12.
Those are divided into 3 groups.
Explanation:
3. Write a division sentence or a number sentence that uses division.
12 counters were divided into ___ groups.
There are ____ counters in each group,
So, 12 ÷ 3 = ____ in each group. ← SAY: Twelve divided by three equals four.
Answer:
The division sentence is 12 ÷ 3 = 4.
There are 4 counters in each group,
So, 12 ÷ 3 = 4 in each group.
Explanation:
Given,
There are 12 counters that were divided into 3 groups.
Therefore we can write the division sentence as 12 ÷ 3 = 4.
So, 12 ÷ 3 = 4 in each group.
SAY: Twelve divided by three equals four.
Try It
Find how many groups. Place 12 counters in groups of 3. How many groups are there?
Answer:
12 ÷ 3 = 4 in each group.
Explanation:
There are 12 counters placed in a group of 3.
12 ÷ 3 = 4 in each group.
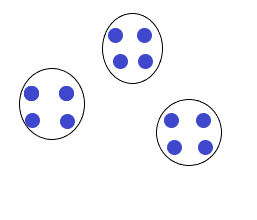
Make groups of 3 until all the counters are gone. Draw the groups.
Answer:
12 ÷ 3 = 4
Explanation:
Write a division sentence. 12 counters were divided into equal groups of ____.
There are ____ groups.
12 ÷ 3 = ____ groups. ← SAY: Twelve divided by three equals four.
Answer:
12 ÷ 3 = 4 groups.
Explanation:
The division sentence is 12 ÷ 3 = 4 groups.
12 counters were divided into equal groups of 4.
Hence there are 4 groups.
12 ÷ 3 = 4 groups.
Talk About It
Question 1.
Explain how you divided 12 counters into equal groups.
Answer:
12 ÷ 3 = 4 in each groups.
Explanation:
Given,
There are 12 counters that are divided into equal groups.
12 ÷ 4 = 3 groups.
Question 2.
When you divided the counters into groups of 3, how did you find the number of equal groups?
Answer:
By dividing the number of counters by the Number of equal groups = The Number in each group.
Explanation:
Number of counters ÷ Number of equal groups = Number in each group
Example:
No of counters = 10
Number of equal groups = 2
Number in each group = No of counters ÷ Number of equal groups
10 ÷ 2 = 5 in each group
Question 3.
Mathematical PRACTICE 3 Draw a Conclusion Explain the difference between the way you partitioned the counters in the first activity to the way you partitioned them in the second activity.
Answer:
In the first activity, the counters are divided with each number of equal groups.
For example
There are 12 counters that were divided into 3 equal groups.
12 ÷ 3 =4 in each group.
Therefore there are 4 equal counters in each group.
Practice It
Question 4.
Partition 8 counters one at a time to find the number of counters in each group. Draw the counters.
There are ___ counters in each group; 8 ÷ 2 = ____.
Answer:
4 counters; 8 ÷ 2 = 4
Explanation:

There are 4 counters in each group
The division sentence is 8 ÷ 2 = 4
Question 5.
Circle equal groups of 5 to find the number of equal groups.

There are ____ equal groups; 15 ÷ ___ = 5.
Answer:
There are 3 equal groups.
15 ÷ 3 = 5.
Explanation:

There are 5 equal groups. I circled equal groups of 5 to find the number of equal groups.
15 ÷ 3 = 5.
Hence the number of equal groups is 5.
Question 6.
Algebra Use counters to find each unknown.
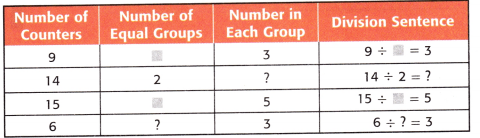
Answer:
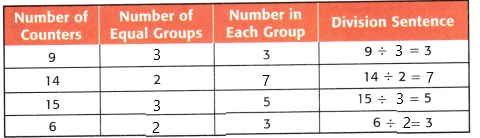
Explanation:
A Division sentence is a number sentence that uses the operation of division.
To find the division sentence
Number of counters ÷ Number of equal groups = Number in each group
9 ÷ 3 = 3
14 ÷ 2 = 7
15 ÷ 3 = 5
6 ÷ 2 = 3
Question 7.
Choose one division sentence from Exercise 6. Write and solve a real-world problem for that number sentence.
Answer:
Let us choose 15 ÷ 3 = 5
The real word problem for that number sentence is 18 ÷ 9 = 2
Explanation:
A Division sentence is a number sentence that uses the operation of division.
To find division sentence
Number of counters ÷ Number of equal groups = Number in each group
Let us choose one division sentence from Exercise 6 is 15 ÷ 3 = 5
Let us assume another division sentence to solve a real-world problem
Number of counters = 18
Number of equal groups = 9
Number in each group = 18 ÷ 9 = 2
Apply It
Draw a mode! to solve. Then write a number sentence.
Question 8.
A florist needs to make 5 equal-sized bouquets from 25 flowers. How many flowers will be in each bouquet?
Answer:
25 ÷ 5 = 5
Explanation:
Given,
No of equal-sized bouquets florist made = 5
No of flowers = 25
To find: How many flowers will be in each bouquet?
25 ÷ 5 = 5
There will be 5 flowers in each bouquet.
Question 9.
Mathematical PRACTICE 4 Model Math Mrs. Wilson called the flower shop to place an order for 9 flowers. She wants an equal number of roses, daisies, and tulips. How many of each kind of flower will Mrs. Wilson receive?
Answer:
9 ÷ 3 = 3
Explanation:
Given,
Mrs. Wilson placed an order for 9 flowers.
There are an equal number of roses, daisies, and tulips = 3
9 ÷ 3 = 3
Hence there are 3 kinds of flowers Mrs. Wilson received.
Question 10.
Mathematical PRACTICE 4 Make a Plan Mr. Cutler bought 2 dozen roses to equally arrange in 4 vases. How many roses will he put in each vase? (Hint: 1 dozen = 12)
Answer:
24 ÷ 4 = 6 roses.
Explanation:
Given,
No of roses Mr. Cutler bought = 2 dozen
1 dozen = 12
2 dozen = 12 × 2 = 24
No of the vases are 4
To find: How many roses will he put in each vase?
24 ÷ 4 = 6 roses.
Hence there are 6 roses he will put in each vase.
Question 11.
Mathematical PRACTICE 2 Reason Can 13 counters be partitioned equally into groups of 3? Explain.
Answer:
No, 13 counters cannot be partitioned equally into groups of 3.
Explanation:
Given,
13 counters.
To be partitioned equally into groups of 3.
13 ÷ 3 = 4.33 which is not possible to partition the counter equally.
Write About It
Question 12.
How can I use models to understand division?
Answer:
The division undoes multiplication and the multiplication undoes division. So we use inverse operation.
Explanation:
For example:
6 × 3 = 18
The division fact is 18 ÷ 6 = 3
McGraw Hill My Math Grade 3 Chapter 5 Lesson 1 My Homework Answer Key
Practice
Question 1.
Partition 6 counters, one at a time, to find the number of counters in each group. Draw the counters.

____ counters were divided into 2 groups; 6 ÷ 2 = ____ counters in each group.
Answer:
There are 3 counters were divided into 2 groups;
6 ÷ 2 = 3 counters in each group.
Explanation:
I have drawn the counters.

There are 3 counters were divided into 2 groups;
6 ÷ 2 = 3 counters in each group.
Question 2.
Circle each group of 4 to find the number of equal groups.

____ counters were divided into groups of 4; 16 ÷ 4 = ___ groups.
Answer:
16 ÷ 4 = 4 groups.
Explanation:
16 counters were divided into groups of 4; 16 ÷ 4 = 4 groups.
Problem Solving
Draw a model to solve. Then write a number sentence.
Question 3.
Nola has 16 bracelets. She hangs an equal number of bracelets on 2 hooks. How many bracelets are on each hook?
Answer:
16 ÷ 2 = 8 bracelets.
Explanation:
Given,
No of the bracelets Nola has = 16
She hangs an equal number of bracelets = 2 hooks
16 ÷ 2 = 8 bracelets.
Hence there are bracelets are on each hook.
Question 4.
Mathematical PRACTICE 4 Model Math Noah rolled 18 large snowballs to make snowmen. He used 3 snowballs for each snowman. How many snowmen did Noah make?
Answer:
18 ÷ 3 = 6 snowmen.
Explanation:
Given,
No of the snowballs Noah rolled to make snowmen = 18
No of snowman he used to make snowman = 3
18 ÷ 3 = 6 snowmen.
Hence there are 6 snowmen Noah made.
Question 5.
There are 8 mittens drying on the heater. Each student has 2 mittens, How many students have mittens drying on the heater?
Answer:
8 ÷ 2 = 4 students have mittens.
Explanation:
Given,
No of mittens drying on the heater = 8
No of the students has mittens = 2
8 ÷ 2 = 4 students have mittens.
Therefore there are 4 students who have mittens drying on the heater.
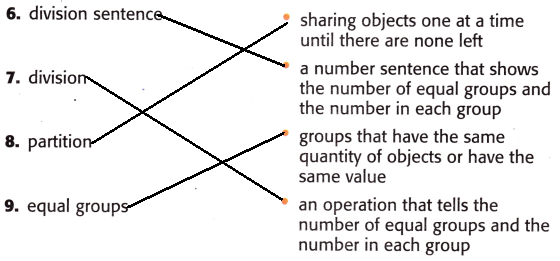
Vocabulary Check
Draw a line to connect each vocabulary word with its definition.

Answer:
I have drawn a line to connect each vocabulary word with its definition.
Explanation: