All the solutions provided in McGraw Hill My Math Grade 3 Answer Key PDF Chapter 13 Lesson 7 Area and the Distributive Property will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 3 Answer Key Chapter 13 Lesson 7 Area and the Distributive Property
Draw It
The grid shows a rectangle with a length of 6 units and a width of 5 units. If the length of this rectangle increased by 2 units, what would be the new area?

The area of the rectangle is ____________ square units.
Label this rectangle A.
1. Shade more unit squares so that the length of the rectangle is now increased by 2 units, but the width remains unchanged.
2. Label the additional rectangle formed by w what you shaded as Rectangle B. What is the area of Rectangle B?
3. Add the areas of rectangles A and B.
The area of the larger rectangle is ______________ square units.

Check: The length of the larger rectangle is 8 units. The width is 5 units. 8 × 5 = 40
Answer:
The area of the rectangle is 30 square units.
Area of rectangle A and B
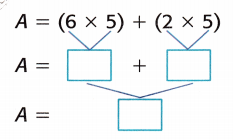
A = (6 × 5) + (2 × 5)
A = 30 + 10
A = 40
The area of the larger rectangle is 40 square units.
Try It
Use the Distributive Property to find the area of the rectangle.
1. Decompose one factor.
12 = 10 + 2
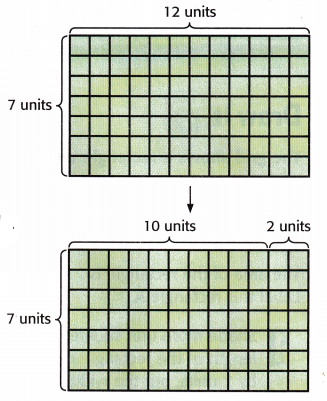
2. Find the area of each smaller rectangle. Then add.
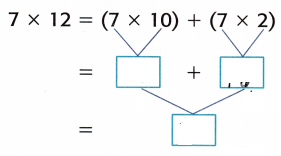
So, the area of the rectangle is ___________ square units.
Answer:
7 × 12 = (7 × 10) + (7 × 2)
= 70 + 14
= 84
So, the area of the rectangle is 84 square units.
Talk About It
Question 1.
Mathematical PRACTICE Justify Conclusions Refer to the second activity. If you decomposed 12 into 9 + 3 instead of 10 + 2, how would that have affected the result?
Answer:
No, it would not have affected the answer.
Question 2.
How can the Distributive Property help you find the area of rectangles with greater numbers?
Answer: It can break up the numbers and help you multiply and add numbers together easily.
Practice It
Use the Distributive Property to find the area of each rectangle.
Question 3.
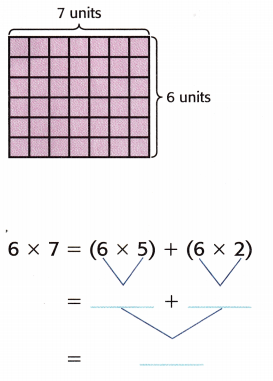
The area is _____________ square units.
Answer:
6 × 7 = (6 × 5) + (6 × 2)
= 30 + 12
= 42
The area is 42 square units.
Question 4.
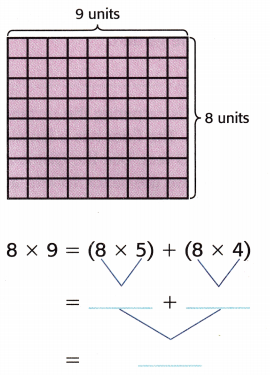
The area is _____________ square units.
Answer:
8 × 9 = (8 × 5) + (8 × 4)
= 40 + 32
= 72
The area is 72 square units.
Find the area of each rectangle. Use the Distributive Property to decompose the longer side into a sum. Show your steps.
Question 5.

The area is _______________ square centimeters.
Answer:
l = 11 cm
w = 4 cm
Area = 11 × 4
= 44 sq. cm
The area is 44 square centimeters.
Question 6.
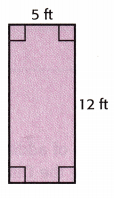
The area is _______________ square feet.
Answer:
l = 5 ft
w = 12 ft
Area = 5 × 12
= 60 sq.ft
The area is 60 square feet.
Apply It
Question 7.
Julia is planting vegetables in her rectangular garden. Her garden has a length of 8 feet and a width of 12 feet. Use the Distributive Property to decompose the factor 12 into a sum. Then find the area of the garden.

Answer:
Given,
Julia is planting vegetables in her rectangular garden. Her garden has a length of 8 feet and a width of 12 feet.
A = 8 × 12
A = (8 × 10) + (8 × 2)
= 80 + 16
= 96 sq. ft
Question 8.
Matthew is carpeting the rectangular floor in his bedroom. The floor has a length of 15 feet and a width of 9 feet. Use the Distributive Property to decompose the factor 15 into a sum. Then find the area of the floor.
Answer:
Given,
Matthew is carpeting the rectangular floor in his bedroom. The floor has a length of 15 feet and a width of 9 feet.
A = 15 × 9
A = (9 × 10) + (9 × 5)
A = 90 + 45
A = 135 sq. ft
Question 9.
Mathematical PRACTICE Reason Describe three ways to find the area of a rectangle with a length of 9 meters and a width of 4 meters.
Answer:
1. A = 9 × 4 = 36 sq .m
2. A = 4 × 9 = 36 sq .m
3. A = (9 × 2) + (9 × 2) = 18 + 18 = 36 sq .m
Question 10.
Mathematical PRACTICE Find the Error James needed to find the area of a rectangle with a length of 11 inches and a width of 9 inches. His steps are to the right. Find and correct his error.
9 × 11 = (9 × 10) + (9 × 2)
= 90 + 18
= 108
Answer:
The mistake happened at 9 × 2, it should have been (9 × 1) + (9 × 10) = 9 + 90 = 99
Write About It
Question 11.
How are the operations of addition and multiplication used when finding area using the Distributive Property?
Answer:
When you break up the numbers you are adding, multiplying the 2 numbers and add the products.
McGraw Hill My Math Grade 3 Chapter 13 Lesson 7 My Homework Answer Key
Practice
Question 1.
Use the Distributive Property to find the area of the rectangle.
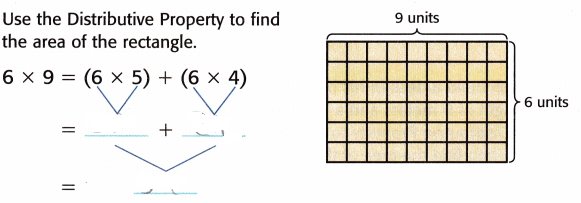
Answer:
6 × 9 = (6 × 5) + (6 × 4)
= 30 + 24
= 54 sq. units
Question 2.
Use the Distributive Property to find the area of the rectangle.
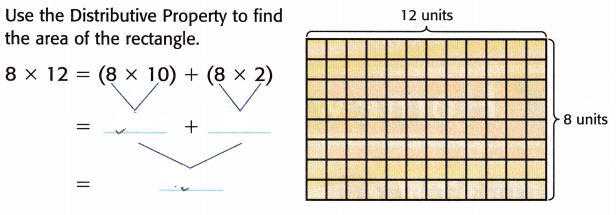
Answer:
8 × 12 = (8 × 10) + (8 × 2)
= 80 + 16 = 96 sq. units
Find the area of each rectangle. Use the Distributive Property to decompose the longer side. Show your steps.
Question 3.
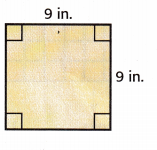
The area is _____________ square inches.
Answer:
s = 9 in.
Area = 9 × 9 = 81
The area is 81 square inches.
Question 4.
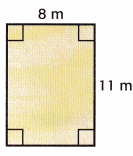
The area is _____________ square meters.
Answer:
l = 8 m
w = 11 m
Area = 8 × 11 = 88
The area is 88 square meters.
Problem Solving
Question 5.
Mathematical PRACTICE Identify Structure Erika is painting a- rectangular painting. The painting has a length of 12 inches and a width of 10 inches. Use the Distributive Property to decompose the factor 12. Then find the area of the painting.
Answer:
Given,
The painting has a length of 12 inches and a width of 10
A = 12 × 10 = 120
Thus the area of the painting is 120 sq. inches
Question 6.
Hector will build a deck in his backyard. The deck ‘has a length of 9 meters and a width of 8 meters. Use the Distributive Property to decompose the factor 9. Then find the area of the deck.
Answer:
Given,
The deck ‘has a length of 9 meters and a width of 8 meters
A = 9 × 8
= 72 sq. meters
Distributive Property
A = (9 × 4) + (9 × 4)
A = 36 + 36
A = 72 sq. meters
Thus the area of the deck is 72 sq. meters