All the solutions provided in McGraw Hill My Math Grade 3 Answer Key PDF Chapter 13 Check My Progress will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 3 Chapter 13 Check My Progress Answer Key
Check My Progress Page No. (777 – 778)
Vocabulary Check
Fill in the correct word(s) that completes the sentence.
area
perimeter
square unit
unit square
Question 1.
The distance around a figure is its _______________.
Answer: The distance around a figure is its perimeter.
Question 2.
A square with a side length of one unit is called a ______________.
Answer: A square with a side length of one unit is called a unit square
Question 3.
______________ is measured in square units and represents the number of those needed to cover a figure without overlapping.
Answer: area is measured in square units and represents the number of those needed to cover a figure without overlapping.
Concept Check
Estimate the perimeter of each figure in centimeters. Then measure the perimeter to the nearest centimeter.
Question 4.

Estimate: _______________
Actual: ______________
Answer:
L = 2 cm
W = 5 cm
Perimeter of the rectangl = 2(L + W)
P = 2(2 + 5)
P = 2 × 10
P = 20 cm
So, estimated perimeter is 20 cm.
Actual perimeter is 20 cm.
Question 5.

Estimate: _______________
Actual: ______________
Answer:
a = 3 cm
b = c = 4
Perimeter of the triangle = 3 + 4 + 4 = 11 cm
So, estimated perimeter is 11 cm.
Actual perimeter is 11 cm
Find the perimeter and area of each figure.
Question 6.
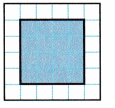
The perimeter is ______________ units.
The area is ______________ square units.
Answer:
s = 4 units
perimeter of a square = 4s
P = 4 × 4 = 16 units
Area of the square = s × s
A = 4 × 4 = 16 sq. units
Question 7.

The perimeter is ______________ units.
The area is ______________ square units.
Answer:
s = 2 units
perimeter of a square = 4s
P = 4 × 2 = 8 units
Area of the square = s × s
A = 2 × 2 = 4 sq. units
Area of the rectangle = 2 × 1 = 2 sq. units
Perimeter of the rectangle = 2(2 + 1) = 2 × 3 = 6
P = 8 + 6 + 6 + 6 + 6 = 32 units
A = 4 + 2 + 2 + 2 + 2 = 12 sq. units
The perimeter is 32 units.
The area is 6 square units.
Question 8.
Algebra Find the unknown side length if 34 in. the perimeter is 89 inches.
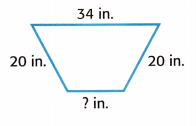
Answer:
P = a + b + c + d
89 = 34 + 20 + 20 + x
x = 89 – 74
x = 15 inch.
Problem Solving
Refer to the drawing at the right for Exercises 9 and 10.
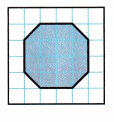
Question 9.
Jeremy will help his father build a patio. The drawing represents the patio. What is the area of the patio in square units?
Answer:
A = 14 sq. units
Question 10.
If each square unit represents 3 square feet, what is the area of the patio in square feet? Use repeated addition.
Answer: 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 = 42 sq. units
Test Practice
Question 11.
Each square unit on the figure represents one square meter. What is the area, in square meters, of the figure?
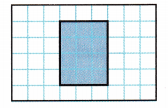
(A) 3 square meters
(B) 6 square meters
(C) 12 square meters
(D) 24 square meters
Answer:
L = 3
W = 4
Area of the rectangle = 3 × 4 = 12 sq. units
Option C is correct.
Check My Progress Page No. (803 – 804)
Vocabulary Check
Question 1.
Circle the figure that represents a composite figure. Explain why the other figures are not composite figures.

Answer:

Question 2.
Circle the formula that can be used to find the area of a rectangle.
A = l + w
A = l – w
A = l × w
Answer:
The formula used to find the area of a rectangle is A = l × w
Concept Check
For Exercises 3 and 4, refer to the rectangle shown.
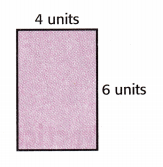
Question 3.
Tile the rectangle to find its area. Draw unit squares on the rectangle.
The area is _____________ square units.
Answer:
L = 4
W = 6
Area of the rectangle = lw
A = 4 × 6 = 24 sq. units
The area is 24 square units.
Question 4.
Algebra Write a multiplication equation that can be used to find the area of the rectangle without tiling it.
Answer:
Area of the rectangle = lw
A = l × w
Question 5.
Algebra Find the area of the rectangle. Write a multiplication equation.
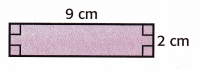
Answer:
L = 9 cm
W = 2 cm
Area of the rectangle = lw
A = 9 × 2 = 18 sq. cm
The area is 18 square cm.
Question 6.
Find the area of the rectangle. Use the Distributive Property to decompose the longer side. Show your steps.
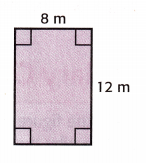
The area is ______________ square meters.
Answer:
L = 8m
W = 12m
Area of the rectangle = lw
A = 8 × 12 = 96 sq. m
The area is 96 square meters
Problem Solving
Refer to the drawing at the right for Exercises 7 and 8.
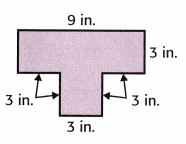
Question 7.
Seth painted the figure at the right on his wall. How many square inches of paint did he use?
Answer:
Figure 1:
L = 9 in
W = 3 in
Area = 9 × 3 = 27 sq. in.
Figure 2:
s = 3 in.
Area = 3 × 3 = 9 sq. in
Area = 27 + 9 = 36 sq. in.
Question 8.
Refer to Exercise 8. Decompose the composite figure in a different way to find its area. Show your steps.
Answer:
Figure 1:
L = 9 in
W = 3 in
Area = 9 × 3 = 27 sq. in.
Figure 2:
s = 3 in.
Area = 3 × 3 = 9 sq. in
Area = 27 + 9 = 36 sq. in.
Test Practice
Question 9.
Which equation can be used to find the area, in square feet, of a rectangle with a length of 8 feet and a width of 4 feet?
(A) 8 + 4 = 12
(B) 8 – 4 = 4
(C) 8 × 4 = 32
(D) 8 ÷ 4 = 2
Answer:
Given,
length = 8 ft
width = 4 ft
Area of the rectangle = 8 × 4 = 32 sq. ft
Option C is the correct answer.