All the solutions provided in McGraw Hill My Math Grade 3 Answer Key PDF Chapter 10 Lesson 8 Compare Fractions will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 3 Answer Key Chapter 10 Lesson 8 Compare Fractions
You can compare fractions when the two fractions refer to the same size whole.
Math in My World
Example 1
Ajay has \(\frac{3}{6}\) of his homework done. Yuki finished \(\frac{4}{6}\) of hers. Who has finished a greater part of their homework?

One Way:
Use fraction tiles.
Compare \(\frac{3}{6}\) and \(\frac{4}{6}\).
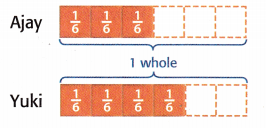
The models show that \(\frac{4}{6}\) has a greater size than \(\frac{3}{6}\).
So, \(\frac{4}{6}\) > \(\frac{3}{6}\).
Another Way:
Use a number line.
Represent each fraction on a number line.

\(\frac{4}{6}\) is closer to 1 whole. So, \(\frac{4}{6}\) > \(\frac{3}{6}\).
So, _____________ finished a greater part of her homework.
Answer:
Given that,
The fractions are \(\frac{4}{6}\), \(\frac{3}{6}\).
So, \(\frac{4}{6}\) > \(\frac{3}{6}\).
So, Ajay finished a greater part of her homework.
Example 2
Camille and Peter were reading a book. Camille read \(\frac{1}{4}\) of the book, while Peter read \(\frac{1}{3}\) of the same book. Who read a greater part of the book?
Compare \(\frac{1}{4}\) and \(\frac{1}{3}\).
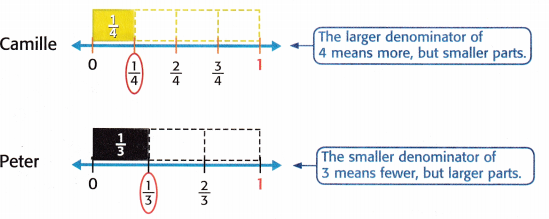
One-third is closer to 1 whole.
So, ![]() is greater than \(\frac{1}{4}\) or
is greater than \(\frac{1}{4}\) or ![]() > \(\frac{1}{4}\).
> \(\frac{1}{4}\).
So, _____________ read a greater part of the book.
Answer:
One-third is closer to 1 whole.
So, 1/3 is greater than \(\frac{1}{4}\) or 1/3 > \(\frac{1}{4}\).
So, Peter read a greater part of the book.
Talk Math
How can you compare two fractions that have the same numerator but different denominators?

Answer:
To compare the fractions with same numerator but different denominators means that fraction is greater than the which as the smaller denominator.
Guided Practice
Question 1.
Use the models to compare. Use >, <, or =.
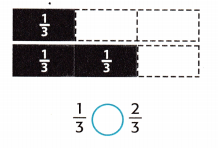
Answer:
Given that the fractions are 1/3, 2/3.
1/3 < 2/3
Independent Practice
Use the models to compare. Use >, <, or =.
Question 2.
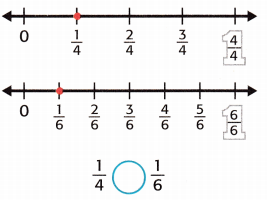
Answer:
Given that,
The fractions are 1/4, 1/6.
1/4 > 1/6.
Question 3.
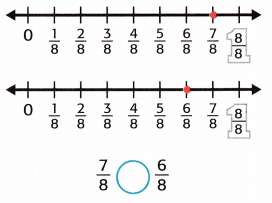
Answer:
Given that,
The fractions are 7/8, 6/8.
7/8 > 6/8
Question 4.
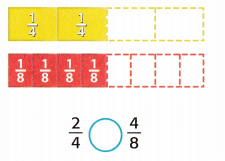
Answer:
Given that,
The fractions are 2/4, 4/8.
2/4 = 4/8.
Question 5.
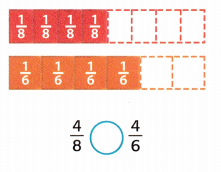
Answer:
Given that,
The fractions are 4/8, 4/6.
4/8 > 4/6
Use the number line for Exercises 6-8.
Question 6.
Circle all of the fractions on the number line that are greater than \(\frac{5}{8}\).
Answer:
Given that the fraction is \(\frac{5}{8}\).
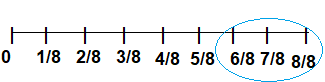
The circle fractions is greater than the 5/8.
Question 7.
Draw a box around all of the fractions on the number line that are less than \(\frac{3}{8}\).
Answer:
Given that the fraction is \(\frac{3}{8}\).
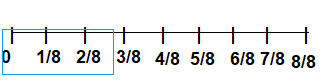
The fractions in the box is less than \(\frac{3}{8}\).
Question 8.
Write the fraction from the number line that is greater than \(\frac{3}{8}\) but less than \(\frac{5}{8}\). ![]()
Answer:
Given that,
The fractions is \(\frac{3}{8}\), \(\frac{5}{8}\).
The fraction greater than \(\frac{3}{8}\) and less than \(\frac{5}{8}\) is \(\frac{4}{8}\).
Problem Solving
Question 9.
Mathematical PRACTICE Explain to a Friend Alister makes a party mix with \(\frac{1}{3}\) cup of raisins and \(\frac{2}{3}\) cup of cereal. Are there more raisins or cereal? Explain.
Answer:
Given that,
Alister makes a party mix with \(\frac{1}{3}\) cup of raisins and \(\frac{2}{3}\) cup of cereal.
\(\frac{1}{3}\) = 1/3 = 0.33.
\(\frac{2}{3}\) = 2/3 = 0.66.
1/3 > 2/3.
Therefore there is more cup of raisins.
Question 10.
Debbie realized that more than 4- of her summer vacation has passed. Circle the fraction that is greater than \(\frac{4}{8}\).
\(\frac{5}{8}\) \(\frac{3}{8}\) \(\frac{2}{8}\)
Answer:
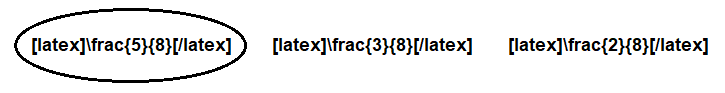
The circle part is greater than the \(\frac{4}{8}\).
HOT Problems
Question 11.
Mathematical PRACTICE Justify Conclusions Is \(\frac{1}{4}\) of the smaller waffle equal to \(\frac{1}{4}\) of the larger waffle? Explain.

Answer:
Given that,
\(\frac{1}{4}\) of the smaller waffle equal to \(\frac{1}{4}\) of the larger waffle.
It means one part of the small waffle is equal to one part of the larger waffle.
Therefore 1/4 = 1/4.
Question 12.
If you are comparing the fractions \(\frac{4}{8}\) and\(\frac{3}{8}\), how can you tell which fraction is greater without using models?
Answer:
Given that,
The fractions are \(\frac{4}{8}\) = 4/8 = 1/2 = 0.5.
\(\frac{3}{8}\) = 3/8 = 0.37
0.5 is greater than 0.37.
\(\frac{4}{8}\) is the greater fraction.
Question 13.
Building on the Essential Question How can fractions be compared?
Answer:
The fractions can be compared using the decimals or using the same denominator.
McGraw Hill My Math Grade 3 Chapter 10 Lesson 8 My Homework Answer Key
Practice
Use the models to compare. Use >, <, or =.
Question 1.
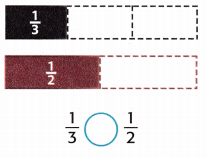
Answer:
Given that,
The fractions are 1/3, 1/2.
1/3 < 1/2
Question 2.
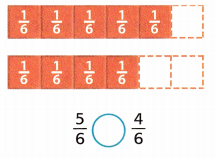
Answer:
Given that,
The fractions are 5/6, 4/6
5/6 > 4/6
Question 3.
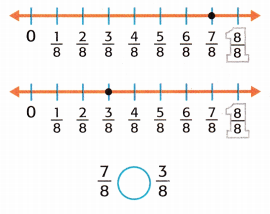
Answer:
Given that,
The fractions are 7/8, 3/8.
7/8 > 3/8.
Question 4.
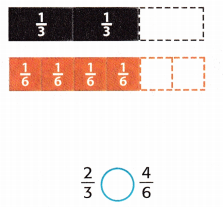
Answer:
Given that,
The fractions are 2/3, 4/6.
2/3 = 4/6.
Problem Solving
Question 5.
Mathematical PRACTICE Justify Conclusions Harvey practiced the piano for \(\frac{5}{8}\) of an hour. Annika practiced the piano for \(\frac{5}{6}\) of an hour. Use the models to determine who practiced the piano for a longer period of time.
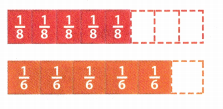
Answer:
Given that,
Harvey practiced the piano for \(\frac{5}{8}\) of an hour.
Annika practiced the piano for \(\frac{5}{6}\) of an hour.
5/6 > 5/8
Therefore the Harvey practiced the piano for longer period of time.
Question 6.
Mathematical PRACTICE Use Math Tools The average housecat sleeps about \(\frac{2}{3}\) of a day. Most people sleep about \(\frac{1}{3}\) of the day. Do housecats or people sleep for a greater fraction of the day? Graph both fractions on the number line to compare.
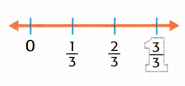
Answer:
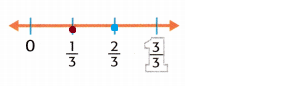
The red dot represents the Most people sleep.
The blue dot represent the average housecat sleeps.
2/3 is greater than 1/3.
Therefore the greater fraction of the day is \(\frac{2}{3}\). it is average housecat sleeps.
Test Practice
Question 7.
The number line shows which of the following fractions is less than \(\frac{2}{4}\)?
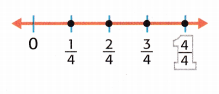
(A) \(\frac{1}{4}\)
(B) \(\frac{2}{4}\)
(C) \(\frac{3}{4}\)
(D) \(\frac{4}{4}\)
Answer:
Given that,
The fraction is \(\frac{2}{4}\).
The fractions less than \(\frac{2}{4}\) is \(\frac{1}{4}\).
Option A is the correct answer.