Long Division With Regrouping And With Remainder is an easy method. It is similar to Long Division With Regrouping And Without Remainder except it has no remainder. This article will include Long Division definition, how to do Long Division With Regrouping And Without Remainder. By going through this article completely you can also check the solved examples for a better understanding of the concept.
Also, Refer:
- Long Division Method without Regrouping with Remainder
- Long Division Without Regrouping and Without Remainder
Long Division – Definition
Long Division is a method used for dividing large numbers into groups or parts. The long division helps in breaking the division problem into a sequence of easier steps. Just like the standard division it also includes terminology like Dividend, divisor, Quotient, Remainder. The number that is being divided by is called Dividend. The number that is being divided is called Divisor. The answer to the division is called Quotient. The remainder is the leftover part after division.
How to do Long Division With Regrouping and With Remainder?
Consider the following steps for doing long division with Regrouping and with the remainder.
- Start with the first digit of the dividend. Divide the digit with a divisor.
- The answer is written as a quotient and subtract the number from the dividend.
- Bring down the next digit right side of the difference.
- Divide the number with a divisor.
- Write the answer as a quotient and subtract the number from the other number.
- Repeat the process. (if a number exists).
Here you can have a look at the solved examples of the long division method with regrouping and with the remainder.
Long Division Method with Regrouping and with Remainder Examples
Example 1:
Divide the numbers 779,2 by long division method with regrouping and with the remainder?
Solution:
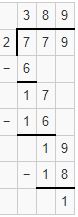
1. Begin with a hundred digit 7, Divide the hundred digit by 2. 7 is not completely divisible by 2. We know that 2*3=6. we will go for it.
7 Hundred÷2 ones=3Hundred.
2. Write the 3 as quotient and subtract the number from the hundred’s digit i.e. 7-6=1.
3. Bring down the tens digit 7 and place it after 1. It becomes 17. Now Divide it by 2.17 is not completely divisible by 2. we know that 2*8=16. We will go for it.
17 Tens÷2 ones=8Ten.
4. Write the 8 as quotient and subtract 16 from the number17 i.e. 17-16=1.
5. Bring down the one’s digit 9 and place it after 1. It becomes 19. Divide it by 2. 19 is not completely divisible by 2. We know that 2*9=18. We will go for it.
19 ones÷2 ones=9 ones
6. Write the digit 9 as quotient and subtract 18 from the number 19 i.e. 19-18=1.
7. Therefore, the division of 779,2 is 389 with 1 as the remainder.
Example 2:
Find the long division of the number 7969 by 3 with regrouping and with the remainder?
Solution:
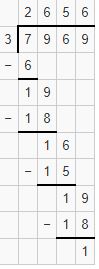
1. Begin with the thousand’s digit 7. Divide it by 3. 7 is not completely divisible by 3.We know that 3*2=6. We will go for it.
7 thousands÷3ones=2thousand.
2. Write 2 as Quotient and subtract 6 from 7 i.e. 7-6=1.
3. Bring down a Hundred digit 9 and place it after 1. It becomes 19. Divide it by 3.19 is not completely divisible by 3 and We know that 3*6=18. We will go for it.
19 Hundred÷3 ones=6 Hundred.
4. Write 6 as Quotient and subtract 18 from 19 i.e. 19-18=1.
5. Bring down tens digit 16. Divide it by 3. 16 is not completely divisible by 3. We know that 3*5=15. We will go for it.
16 Tens÷3 ones=5 Tens.
6. Write 5 as Quotient and subtract 15 from 16 i.e. 16-15=1.
7. Bring down One’s digit 9 and place it after 1. It becomes 19. Divide it by 3. 19 is not completely divisible by 3. We know that 3*6=18.
19 Ones÷3 ones=6 ones.
8. Write 6 as Quotient and 1 as the remainder.
Therefore, the division of 7969÷3 is 2656 with 1 as the Remainder.
Example 3:
Find the long division of the number 4936 by 3 with regrouping and with the remainder?
Solution:
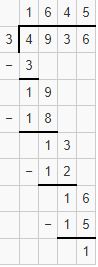
1. Begin with the thousand’s digit 4. Divide it by 3. 4 is not completely divisible by 3. We know that 3*1=3. We will go for it.
4 thousands÷3ones=1thousand.
2. Write 1 as Quotient and subtract 3 from 4 i.e. 4-3=1.
3. Bring down a Hundred digit 9 and place after 1. It becomes 19. Divide it by 3. 19 is not completely divisible by 3. We know that 3*6=18. We will go for it.
19 Hundred÷3 ones=6Hundred.
4. Write 6 as Quotient and subtract 18 from 19 i.e. 19-18=1.
5. Bring down tens digit 3 and place it after 1. It becomes 13. Divide it by 3. We know 13 is not completely divisible by 3. We know that 3*4=12. We will go for it.
13 Tens÷3 ones=4 Tens.
6. Write 4 as Quotient and subtract 12 from 13 i.e. 13-12=1.
7. Bring down One’s digit 6 and place it after 1. It becomes 16. Divide it by 3. We know that 3*5=15. We will go for it.
16 Ones÷3 ones=5 ones.
8. Write 5as Quotient and 1 as the remainder.
Therefore, the division of 5937÷3 is 1979 with 1 as the remainder.
Example 4:
Find the long division of the number 3759 by2 with regrouping and with the remainder?
Solution:
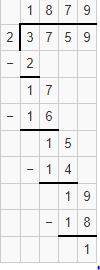
1. Begin with the thousand’s digit 3. Divide it by 2.
3 thousands÷2ones=1thousand.
2. Write 1 as Quotient and subtract 2 from 3 i.e. 3-2=1.
3. Bring down a Hundred digit 7 and place it after 1. It becomes 17. Divide it by 2. 17 is not completely divisible by 2, We know that 2*8=16. We will go for it.
17 Hundred ÷2 ones=8 Hundred
4. Write 8 as Quotient and subtract 16 from 17 i.e. 17-16=1.
5. Bring down tens digit 5 and place it after 1. It becomes 15. Divide it by 2. 15 is not completely divisible by 2. We know that 2*7=14.
15Tens÷2 ones=7 Tens.
6. Write 7 as Quotient and subtract 14 from 15 i.e. 15-14=1.
7. Bring down One’s digit 9 and place it after 1. It becomes 19. Divide it by 2.
19 Ones÷2 ones=9 ones.
8. Write 9 as Quotientwith remainder 1.
Therefore, the division of 3759÷2 is 1879 with 1 as the remainder.
Example 5:
Find the long division of 9399,2 with regrouping and with the remainder?
Solution:
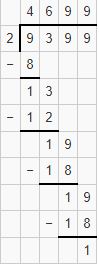
1. Begin with the thousand’s digit 9. Divide it by 2. 9 is not completely divisible by 2. We know that 2*4=8. We will go for it.
9 thousands÷2ones=4thousand.
2. Write 4 as Quotient and subtract 8 from 9 i.e. 9-8=1.
3. Bring down a Hundred digit 3 and place it after 1. It becomes 13. Divide it by 2.since 13 is not completely divisible by 2, we will go for 2*6=12.
13 Hundred÷2 ones=6Hundred.
4. Write 6 as Quotient and subtract 12 from 13 i.e. 13-12=1.
5. Bring down tens digit 9 and place it after 1. It becomes 19. Divide it by 2. 19 is not completely divisible by 2. We know that 2*9=18. We will go for it.
19 Tens÷2 ones=9 Tens.
6. Write 9 as Quotient and subtract 18 from 19 i.e. 18-19=1.
7. Bring down One’s digit 9 and place it after 1. It becomes 19. Divide it by 2.19 is not completely divisible by 2. We know that 2*9=18. We will go for it.
19 Ones÷2 ones=9 ones.
8. Write 9 as Quotient and 1 as the Remainder.
Therefore, the division of 9399÷2 is 4699 with the remainder as 1.