We included HMH Into Math Grade 8 Answer Key PDF Module 7 Review to make students experts in learning maths.
HMH Into Math Grade 8 Module 7 Review Answer Key
Vocabulary
elimination
substitution
system of
equations
Choose the correct term from the Vocabulary box.
Question 1.
A ____ is two or more equations that contain two or more variables.
Answer: A system of equations is two or more equations that contain two or more variables.
Question 2.
A method of solving a system of equations that involves adding system equations to remove a variable is called ____
Answer: A method of solving a system of equations that involves adding system equations to remove a variable is called elimination.
Question 3.
A method of solving a system of equations that involves replacing a variable with a number or another expression is called _____
Answer: A method of solving a system of equations that involves replacing a variable with a number or another expression is called substitution.
Concepts and Skills
Question 4.
North Shore Kayak and South Shore Kayak each charge a flat fee plus an hourly rate. The graph shows y, the cost in dollars, for renting a kayak from each company for x hours. Which statement about the companies is true?
A. The companies have the same hourly rate.
B. South Shore costs more when renting a kayak for 2 hours.
C. The flat fee is higher for North Shore than for South Shore.
D. The companies cost the same when renting a kayak for 1 hour.
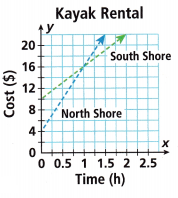
Answer: D. The companies cost the same when renting a kayak for 1 hour.
Question 5.
A graph of a system of two equations is shown. What is the solution of the system? Write the ordered pair.
(_____, _____)
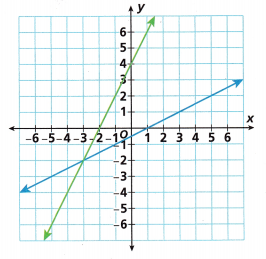
Answer:
A solution to a system of equations is a set of values for the variable that satisfy all the equations simultaneously.
In the above graph, we can see that two equations meet at the point (-3, -2)
So, the ordered pair is (-3, -2)
Question 6.
Use Tools Determine the solution of the system of equations shown. State what strategy and tool you will use to answer the question, explain your choice, and then find the answer.
y = x + 1
y = -2x + 4
Answer:
y = x + 1
y = -2x + 4
Substitute y = -2x + 4
-2x + 4 = x + 1
-2x – x = 1 – 4
-3x = -3
x = 1
Substitute x = 1 in the above equation
y = x + 1
y = 1 + 1
y = 2
The solution of system of equations are y = 2 and x = 1.
Determine the solution of each system of equations.
Question 7.
y = -6x + 4
y = 2 + 12 (___, ____)
Answer:
y = -6x + 4
y = 2 + 12
y = 14
Substitute y = 14 in the above equation.
14 = -6x + 4
14 – 4 = -6x
10 = -6x
x = -10/6
x = -5/3
Question 8.
3x + 2y = 9
4x – y = 34 (___, ____)
Answer:
3x + 2y = 9
4x – y = 34
3x + 2y = 9
3x = 9 – 2y
x = (9-2y)/3
4[(9-2y)/3] – y = 34
[(36-11y)/3 = 34]
36 – 11y = 34 × 3
36 – 11y = 102
-11y = 102 – 36
-11y = 66
y = -66/11
y = -6
3x + 2y = 9
3x + 2(-6) = 9
3x -12 = 9
3x = 9 + 12
3x = 21
x = 21/3
x = 7
Thus the solutions to the system of equations are x = 7 and y = -6.
Question 9.
A system of equations is shown. Which method could be used to eliminate a variable from the system?
5x + 6y = 28
4x + 2y = 14
A. Multiply the first equation by -4, and then add the equations.
B. Multiply the first equation by -2, and then add the equations.
C. Multiply the second equation by -3, and then add the equations.
D. Multiply the second equation by -2, and then add the equations.
Answer: C. Multiply the second equation by -3, and then add the equations.
5x + 6y = 28
4x + 2y = 14—- × (-3)
-12x – 6y = -42
5x + 6y – 28 -12x -6y + 42 = 0
-7x + 14 = 0
14 = 7x
x = 2
Question 10.
Select the number of solutions for each system of two linear equations.
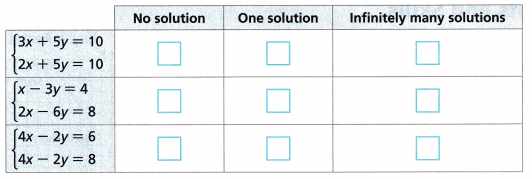
Answer:
i. 3x + 5y = 10
2x + 5y = 10
3x + 5y – 10 = 2x + 5y -10
3x + 5y -10 – 2x – 5y + 10 = 0
x = 0
It has infinite number of solutions.
ii. x – 3y = 4 ⇒ x – 3y – 4 = 0
2x – 6y = 8 ⇒ 2x – 6y – 8 = 0
x – 3y -4 – 2x + 6y + 8 = 0
-x + 3y + 4 = 0
x = 3y + 4
2 (3y + 4) + 5y = 10
6y + 8 + 5y = 10
11y + 8 = 10
11y = 2
y = 2/11
x – 3(2/11) = 4
x – 6/11 – 4 = 0
x – 4.54 = 0
x = 4.54
It has one solution.
iii. 4x – 2y = 6
4x – 2y = 8
4x – 2y – 6 – 4x + 2y + 8 = 0
-6 + 8 = 0
2 = 0
It has no solution.
Question 11.
Tickets for a high school basketball game cost $4 for adults and $3 for students. The school sells 120 tickets and makes $412 in ticket sales. The system of equations shown can be used to determine the number of adult tickets a and the number of student tickets s the school sold. How many adult tickets and how many student tickets did the school sell?
a + s = 120
4a + 3s = 412
____ adult tickets ____ student tickets
Answer:
Given,
Tickets for a high school basketball game cost $4 for adults and $3 for students.
The school sells 120 tickets and makes $412 in ticket sales.
a + s = 120— × 3 = 3a + 3s = 360
4a + 3s = 412
3a + 3s – 360 – 4a – 3s – 412 = 0
-a – 772 = 0
a = -772
Substitute a = -772 in the given equation
-772 + s = 120
s = 120 + 772
s = 892
772 adult tickets and 892 student tickets.
Question 12.
Corinne’s pumpkin weighs 28 ounces and is growing at a rate of 5 ounces per week. Ron’s pumpkin weighs 10 ounces and is growing at a rate of 13 ounces per week. Let t represent time in weeks and w represent weight in ounces. Which system of equations can be used to determine when the weights of the two pumpkins will be equal?
A.
w = 5 + 28t
w = 13 + 10t
B.
w = 5(t + 28)
w = 13(t + 10)
C.
w = 5t – 28
w = 13t – 10
D.
w = 5t + 28
w = 13t + 10
Answer:
Given,
Corinne’s pumpkin weighs 28 ounces and is growing at a rate of 5 ounces per week.
Ron’s pumpkin weighs 10 ounces and is growing at a rate of 13 ounces per week.
Let t represent time in weeks and w represent weight in ounces.
Corrine’s: w = 28 + 5t
Ron’s: w = 10 + 13t
So, the system of equations is
w = 5t + 28
w = 3t + 10
Option D is the correct answer.