Into Math Grade 8 Module 7 Lesson 6 Answer Key Apply Systems of Equations

We included HMH Into Math Grade 8 Answer Key PDF Module 7 Lesson 6 Apply Systems of Equations to make students experts in learning maths.

HMH Into Math Grade 8 Module 7 Lesson 6 Answer Key Apply Systems of Equations

I Can write and solve a system of equations to solve a real-world problem.

Step It Out

Question 1.
There are 12 people in an adventure club going to an adventure park. An adult’s pass is $55, a child’s pass is $42, and they spend a total of $569. How many adults and how many children go together to the park?

A. What equation can you write to represent the number of adults a and children c that are in the group?
+ = 12
Answer:
a + c = 12,

Explanation:
Given there are 12 people in an adventure club going to an adventure park. An adult’s pass is $55,
a child’s pass is $42 and they spend a total of $569, The equation I can write to represent the number of adults a and children c that are in the group are a + c = 12.

B. How much is an adult’s pass? How much is a child’s pass? What was the total spent on day passes?
What equation can you write to represent the total amount spent by the group?
a + c =
Answer:
Adult pass is $55, Child’s pass is $42 and Total spent on day passes is $569,
Equation: 55a  + 42c = 569,

Explanation:
Adult pass is $55, Child’s pass is $42 and Total spent on day passes is $569,
Equation to represent the total amount spent by the group is 55a  + 42c = 569.

C. You can use the two equations from Parts A and B to write a system of equations to solve the problem. Write the system of equations.
+ = 12
a + c =
Answer:
System of equations: a + c = 12 and 55a  + 42c = 569,

Explanation:
The two equations from Parts A and B to write a system of equations to solve the problem is
a + c = 12 and 55a  + 42c = 569.

D. Solve the system of equations using elimination.
a =
c =
Answer:
a = 5 and  c= 7,

Explanation:
Solving the system of equations: a + c = 12 and 55a  + 42c = 569 as a = 12 – c, substituting in
55a + 42c = 569, 55(12 – c) + 42c = 569, 660 – 55c + 42c = 569, 660 – 13c = 569,
13c = 660 – 569, 13c = 91, c = 91/13 = 7, Now a = 12 – 7 = 5, therefore a = 5, c = 7.

E. How many adults and how many children go together to the park?
__________ adults
__________ children
Answer:
5 adults and 7 children go together to the park,

Explanation:
Got a = 5, c = 7 means 5 adults and 7 children go together to the park.

Turn and Talk Is there another way to solve the system of equations? Explain.
Answer:
Yes,

Explanation:
Solving the system of equations: a + c = 12 and 55a  + 42c = 569 as c = 12 – a,
substituting in 55a + 42c = 569 as 55a + 42(12 – a) = 569, 55a + 504 – 42a = 569,
13a + 504 = 569, 13a = 569 – 504, 13a = 65, a = 65/13 = 5, substituting a = 5 in c = 12 – a,
we get c = 12 – 5 = 7.

Question 2.
Kailee is holding an event at a ballroom with tables that seat 6 people and tables that seat 4 people. Kailee orders a total of 12 tables for the 57 people coming to the event. How many tables of each kind should she order?

A. Let x represent the number of tables that seat 6 people and y represent the number of tables that seat 4 people. Complete the equation to represent the total number of tables.
+ =
Answer:
x + y = 12,

Explanation:
Given Kailee is holding an event at a ballroom with tables that seat 6 people and tables that seat 4 people. Kailee orders a total of 12 tables for the 57 people coming to the event. If x represent the number of tables that seat 6 people and y represent the number of tables that seat 4 people. The equation to represent the total number of tables are x + y = 12.

B. Complete the equation that represents the seating capacity of the tables Kailee orders, relative to her seating needs.
x + y = 57
Answer:
6x + 4y = 57,

Explanation:
Completed the equation that represents the seating capacity of the tables Kailee orders relative to her
seating needs as 6x + 4y = 57.

C. These two equations comprise the system of equations that represent the problem. Begin solving the system of equations by first solving one equation for y.
x + y = 12 → y =
Substitute the resulting expression for y into the second equation and solve for x.

Answer:

Explanation:
These two equations comprise the system of equations that represent the problem. Begin solving the system of equations by first solving one equation for y.
x + y = 12 → y = 12 – x, Substituting the resulting expression for y into the second equation and solving for x as 6x + 4(12 – x) = 57, 6x + 48 – 4x = 57, 2x = 57 – 48, 2x = 9, x = 9/2.

D. Does the value for x make sense for this problem? Why or why not?
Answer:
Yes,

Explanation:
Yes, the value of x = 9/2 make sense for this problem as y = 12 – x, we have y = 12 – 9/2 = 24 – 9/2 = 15/2, now checking x and y so we get 9/2 + 15/2 = (9 + 15)/2 = 24/2 = 12 which is same as x + y = 12.

E. Round the value for x up to the nearest whole number, and use that value to solve for y.
+ y = 12 → y =
She should order ___________ tables that seat 6 people and tables that seat 4 people.
Answer:
4 + y = 12, y = 8,
She should order 4 tables that seat 6 people and 8 tables that seat 4 people,

Explanation:
Rounding the value for x up to the nearest whole number and using that value to solve for y as x= 4.5 to 4, 4 + y = 12, y = 8, She should order 4 tables that seat 6 people and 8 tables that seat 4 people.

F. Substitute x and y into the second equation. If Kailee orders these tables, will she have enough seats for all attendees? Explain.
7() + 5() =
Answer:
7 X 4 + 5 X 8 = 68, Yes, she will have enough seats for all attendees,

Explanation:
Substituting x = 4 and y = 8 into the second equation 7 X 4 + 5 X 8 = 28 + 40 = 68 therefore if Kailee orders these tables, she will have enough seats for all attendees.

Turn and Talk If a value doesn’t make sense for the solution to a problem, do you always round the value up? Explain.
Answer:
Yes,

Explanation:
Yes, if a value doesn’t make sense for the solution to a problem, I do always round the value up because the final answer should always be rounded to reflect the number of significant digits in the result and normally I would not want to round before that if I can help it. If I am using a computer or calculator I should avoid using numbers that have been rounded as much as possible. Even if I round my final answer, I should store the “exact” value for future computations.

Question 3.
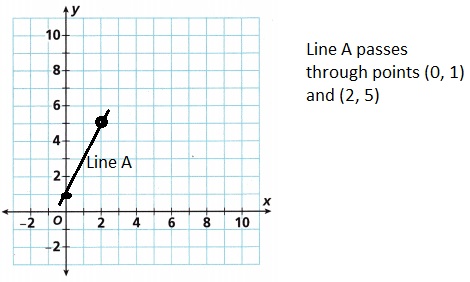
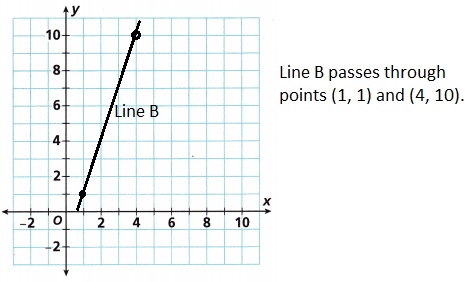
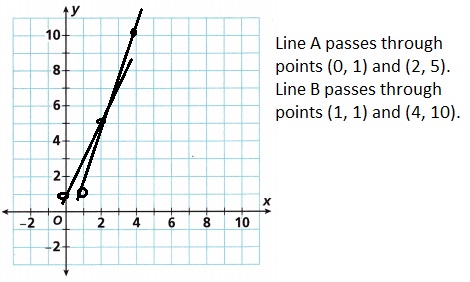
Line A passes through points (0, 1) and (2, 5). Line B passes through points (1, 1) and (4, 10).

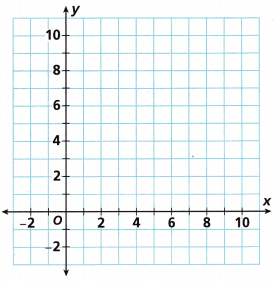
A. Plot the points for Line A and draw a line through them.
Answer:

Explanation:
Plotted the points (0, 1) and (2, 5) for Line A and drawn a line through them as shown above.

B. Plot the points for Line B and draw a line through them.
Answer:

Explanation:
Plotted the points (1, 1) and (4, 10) for Line B and drawn a line through them as shown above.

C. Do the lines intersect?
Answer:

Yes,

Explanation:
Yes the lines intersect.

D. Use the graph to estimate the point of intersection.
Answer:
(2,5),

Explanation:
Used the graph to estimate the point of intersection as (2,5).

E. How could you find the exact point of intersection?
Answer:
By using the graph where the point intersects,

Explanation:
I could find the exact point of intersection, By seeing the graph at which the point gets exactly intersected.

Check Understanding

Write and solve a system of equations to solve Problems 1-3.

Question 1.
The Spartan basketball team scored 108 points in last night’s game. They scored 48 baskets in all, making a combination of two-point and three-point baskets. There were no points due to free throws. How many three-point baskets did the Spartans make?
Answer:
System of equations are x + y = 48 and 2x + 3y = 108,
Three-point baskets did the Spartans make are 12,

Explanation:
Given the Spartan basketball team scored 108 points in last night’s game. They scored 48 baskets in all, making a combination of two-point and three-point baskets.
There were no points due to free throws, the system of equations are x + y = 48 equation (1) and 2x + 3y = 108 equation(2), Solving eqaution (1) x= 48 – y, Substituting x in equation(2) we get 2(48 – x) + 3 y = 108, 96 – 2x + 3y = 108, y + 96 = 108, y = 108 – 96, y = 12, Now x = 48 – 12 = 36, therefore three-point baskets did the Spartans make are 12.

Question 2.
Mr. Chen buys 5 tomato plants and 3 cucumber plants for $33.00. His neighbor buys 4 tomato plants and 2 cucumber plants of the same varieties for $24.90 at the same nursery. What is the cost of each type of plant?

Answer:
System of equations are 5t + 3c = 33, 4t + 2c = 24.90, Cost of tomato plant is $4.35 and
cost of cucumber plant is $3.75,

Explanation:
Given Mr. Chen buys 5 tomato plants and 3 cucumber plants for $33.00. His neighbor buys
4 tomato plants and 2 cucumber plants of the same varieties for $24.90 at the same nursery.
Let tomato plant be t and cucumber plant be c, the system of equations are 5t + 3c = 33 equation(1)
4t + 2c = 24.90 equation(2), Multiplying equation 1 by 2 and equation 2 by 3 and
subtracting equation (2) from (1) we get
12t + 6c = 74.7
-10t – 6c = 66.0
2t = 8.7, so t = 8.7/2 = 4.35 now substituting t in equation 1 we get 5 X 4.35 + 3c = 33,
21.75 + 3c = 33, 3c = 33 – 21.75 = 11.25, c = 11.25/3 = 3.75, therefore cost of tomato plant is $4.35 and cost of cucumber plant is $3.75.

Question 3.
One line passes through (0, 1) and (4, -7). A second line passes through (-1, -1) and (1, -5). Do the two lines intersect? If so, where? Show your work.
Answer:

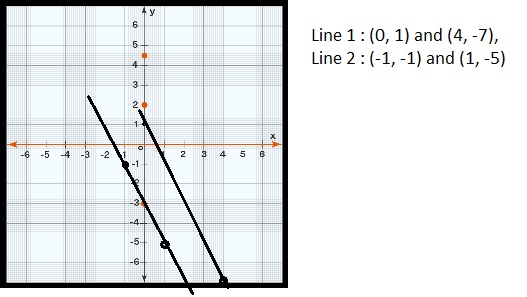
Explanation:
Given one line passes through (0, 1) and (4, -7) and a second line passes through (-1, -1) and (1, -5).
The two lines intersect do not intersect each other.

On Your Own

Question 4.
Model with Mathematics A museum charges different rates for adults and students. Mrs. Lopez’s class went to the museum last week and spent $232.50 on 25 tickets. How many students and how many adults went to the museum?

A. Write a system of equations to model the problem.
Answer:
System of equations to model the problem is a + s = 25, 14.50a + 8s = 232.50,

Explanation:
Given a museum charges different rates for adults and students. Mrs. Lopez’s class went to
the museum last week and spent $232.50 on 25 tickets, Let a be the adults and s be the students,
System of equations to model the problem is a + s = 25, 14.50a + 8s = 232.50.

B. Find the solution using any method.
Answer:
a = 5, s = 20,

Explanation:
The solution using method is solving equations a + s = 25 equation (1),
14.50a + 8s = 232.50 equation (2) we get a = 25 – s, substituting in equation (2) we get
14.50(25 – s) + 8s = 232.50, 362.50 – 14.50s + 8s = 232.50, 362.50 -232.50 = 6.5s,
130 = 6.5 s, s = 130/6.5 = 20, now a = 25 – 20 = 5.

C. What is the meaning of the solution in the context of the problem?
Answer:
Number of adults who went to the museum are 5 and number of students who went to the museum are 20,

Explanation:
The meaning of the solution in the context of the problem are number of adults who went to the museum are 5 and number of students who went to the museum are 20.

Question 5.
Tony is hiking on a trail when he sees his friend Nathan 30 feet in front of him.

A. Graph a system of equations modeling the situation.

Answer:
System of equations modeling the situation: n = t + 30, n = 4, t = 2,

B. Will Tony catch up to Nathan? Explain.
Answer:

Question 6.
Model with Mathematics The sum of two numbers is 18. The sum of the greater number and twice the lesser number is 25.
A. Let x represent the greater number and y represent the lesser number. Write a system of equations to find the numbers.
Answer:
System of equations are x + y = 18, x – 2y = 25,

Explanation:
Given the sum of two numbers is 18. The sum of the greater number and twice the lesser number is 25. Let x represent the greater number and y represent the lesser number.
The system of equations to find the numbers are x + y = 18 and x – 2y = 25.

B. Solve the system. What are the two numbers?
Answer:
The two numbers are x = 61/3 and y = -7/3,

Explanation:
Solving the system of equations x + y = 18 equation (1) and x – 2y = 25 equation (2) substituting x = 18 – y in equation(2) we get (18 – y) – 2y = 25, 18 – y – 2y = 25, 18 – 3y = 25, -3y = 25 – 18 = 7,
y = -7/3, x = 18 + 7/3 = 54 + 7/3 = 61/3, Therefore the two numbers are x = 61/3 and y = -7/3.

Question 7.
Two angles are complementary if the sum of their measures is equal to 90°. Georgia draws two complementary angles. One of the angles measures 15° more than 2 times the other angle’s measure.

A. Model with Mathematics Write a system of equations to represent the situation.
Answer:
System of equations: x + y = 90°, y = 2x + 15°,

Explanation:
Given two angles are complementary if the sum of their measures is equal to 90°. Georgia draws two
complementary angles. One of the angles measures 15° more than 2 times the other angle’s measure.
Let x be one angle and y be another angle, System of equations to represent the situation are
x + y = 90°, y = 2x + 15°.

B. What are the measures of the two angles?
Answer:
x = 25° and y = 75°,

Explanation:
The measures of the two angles are solving the system of equations x + y = 90°,
y = 2x + 15°, substituting y value as x + 2x + 15° = 90°, 3x + 15° = 90°, 3x = 90° – 15°,
3x = 75°, x = 75°/3 = 25°, So y = 2 X 25° + 15° = 50°+ 15° = 75°. Therefore the measures of the
two angles are x = 25° and y = 75°.

Question 8.

Open-Ended Write a problem that could be solved using the graph shown. Explain what happens and how it relates to the solution.

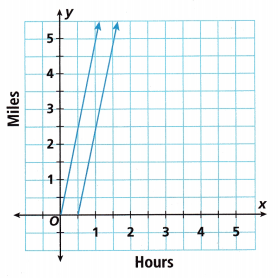
Answer:
Line 1 : y = 5x – 0.5, Line 2 : y = 5x -3, The two lines are parallel as their slopes are equal,

Explanation:
We have two lines one line1 is with points (0.5,2),(1,4.5) and line 2 is with points (1,2), (1.5,4.5),
slope for line 1 is 4.5 – 2/1-0.5 = 2.5/0.5= 5, y-intercept is 2 = 5(0.5) + b,
b= 2 – 2.5 = – 0.5, Equation of line 1 is y = 5x – 0.5, slope for line 2 is 4.5 – 2/1.5 – 1 = 2.5/0.5 = 5,
y-intercept is 2 = 5(1) + b, b = 2 – 5 = -3, Equation of line 2 is y = 5x -3, As the two lines have same slope the lines are parallel to each other.

Question 9.
Reason Mrs. Bennett gives her math class a test worth 145 points. Some of the questions are worth two points and some are worth five points. Is there enough information to determine how many five-point questions are on the test? If so, how many? If not, what additional information is needed?
Answer:
No, there is not enough information, Number of questions in the test,

Explanation:
Given Mrs. Bennett gives her math class a test worth 145 points. Some of the questions are
worth two points and some are worth five points.
There is not enough information to determine how many five-point questions are on the test.
The additional information needed is number of questions in the test.

Question 10.
The Fairplay sporting goods store sells two different models of a popular fitness tracker. In one month the store sold 42 trackers for a total of $6574.

A. Model with Mathematics Write a system of equations that represents the situation.
Answer:
System of equations: A + B = 42, 127A + 189B = 6574,

Explanation:
Given the Fairplay sporting goods store sells two different models of a popular fitness tracker.
In one month the store sold 42 trackers for a total of $6574.
and model A sells each at $127 and model B sells at $189, So system of equations are A + B = 42 and
127A + 189B = 6,574.

B. How many of each type of tracker were sold?
Answer:
Model A type of tracker 22 were sold, Model B type of tracker 20 were sold,

Explanation:
Solving system of equations: A + B = 42 and 127A + 189B = 6574 we get B = 42 – A substituting
value of B in 127A + 189(42 -A) = 6574, 127A + 7,938 – 189A = 6,574, 7,938 – 6,574 = 62A,
62A = 1,364, A = 1,364 ÷ 62 = 22, So B = 42 – 22 = 20, therefore model A type of tracker 22 were sold and model B type of tracker 20 were sold.

Question 11.
Bowling costs $6 per game and virtual golf costs $0.50 per hole. Bowling takes 30 minutes per game and virtual golf takes 7.5 minutes per hole. Toni spends 1 hour and $8 between the two activities.
A. Model with Mathematics Write a system of equations relating b, the number of games of bowling played, to g, the number of holes of virtual golf played.
Answer:
System of equations is 6b + 0.5g = 8, 30b + 7.5g = 60,

Explanation:
Given bowling costs $6 per game and virtual golf costs $0.50 per hole. Bowling takes 30 minutes per
game and virtual golf takes 7.5 minutes per hole.
Toni spends 1 hour and $8 between the two activities. Modelling with Mathematics writing a system of equations relating b the number of games of bowling played,
to g the number of holes of virtual golf played as 6b + 0.5g = 8, 30b + 7.5g = 60.

B. Solve the system you wrote and interpret your solution.
Answer:
Number of games of bowling played are 1,
Number of holes of virtual golf played 4,

Explanation:
Solving the system of equations is 6b + 0.5g = 8, 30b + 7.5g = 60,
6b = 8 – 0,5g, b = (8 – 0.5g)/6, Substituing as 30(8 – 0.5g)/6 +7.5g = 60,
5(8 – 0.5g) + 7.5g = 60, 40 – 2.5g + 7.5g = 60, 5g = 60 – 40 = 20, g = 20/5 = 4,  now b = (8 – 0.5 X 4)/6, b = 8 – 2/6= 6/6 = 1, therefore number of games of bowling played are 1,
number of holes of virtual golf played 4.

Question 12.
The table shows two options provided by an internet service provider.

A. Model with Mathematics Write a system of equations modeling this situation, where c represents the total cost for m months of service.
Answer:
System of equation are c = 100 + 55m, c = 30 + 75m,

Explanation:
Given two options provided by an internet service provider,
System of equations modeling this situation, where c represents the total cost for m months of service are c = 100 + 55m, c = 30 + 75m.

B. After how many monthly payments will the cost of the two options be the same? Explain.
Answer:
3.5 months,

Explanation:
The cost of the two options will be the same after equating both equations and solving as 100 + 55m = 30 + 75m, 100 – 30 = 75m – 55m, 70 = 20m, m = 70/20 = 3.5, therefore the cost of two options will be the same after 3.5 months.

C. Construct Arguments Which option would you recommend for someone who is only going to stay in town for 5 months? Why?
Answer:
Option 1,

Explanation:
To recommend for someone who is only going to stay in town for 5 months checking with both options as 1. c = 100 + 55m, c = 100 + 55 X 5 = 100 + 275 = $375,
2. c = 30 + 75m = 30 + 75 X 5 = 30 + 375 = $405, As option 1 is less than option 2 so we recommend
option 1.

Question 13.
Model with Mathematics Alicia bought 4 sandwiches and 5 bowls of soup, spending $38.50. Adam spent $47.25 to buy three sandwiches and nine bowls of soup. Write and solve a system of equations to find out the cost of each sandwich and each bowl of soup.

Answer:
System of equations: 4s + 5b = 38.50, 3s + 9b = 47.25, Cost of sandwich is $5.25,
cost of bowl of soup is $3.5,

Explanation:
Given Alicia bought 4 sandwiches and 5 bowls of soup, spending $38.50. Adam spent $47.25 to buy three sandwiches and nine bowls of soup. Writing and solving a system of equations to find out the cost of each sandwich and each bowl of soup as let s be cost of sandwiches and
b be cost of bowl of soup so 4s + 5b = 38.50, 3s + 9b = 47.25, s = 47.25 – 9b/3,
Substituting 4(47.25 – 9b)/3 + 5b = 38.50, 4(47.25 – 9b) + 15b = 38.50 X 3,
189 – 36b + 15b = 115.5, 189 – 115.5 = 21b, 73.5 = 21b, b = 73.5/21 = 3.5, Now s = 47.25 – 9 X 3.5/3,
s = 47.25 – 31.5/3 = 15.75/3 = 5.25. Therefore cost of sandwich is $5.25 and cost of bowl of soup is $3.5.

Lesson 7.6 More Practice/Homework

Question 1.
A builder is developing a neighborhood of one-bedroom and two-bedroom houses. The builder wants to build 12 houses and has 88 windows. The one-bedroom houses need 6 windows and the two-bedroom houses need 9 windows.

A. Model with Mathematics Write and solve a system of equations to represent the situation.
Answer:
System of equations: o + t = 12, 6o + 9t = 88,

Explanation:
Given a builder is developing a neighborhood of one-bedroom and two-bedroom houses.
The builder wants to build 12 houses and has 88 windows. The one-bedroom houses need
6 windows and the two-bedroom houses need 9 windows.
Let o be one-bedroom houses and t be two-bedroom houses, System of equations are o +  t = 12,
6o + 9t = 88.

B. How many of each type of house should the builder build?
Answer:
One-bedroom houses – 20/3, Two-bedroom houses – 16/3,

Explanation :
To find each type of house should the builder build are solving o +  t = 12,
6o + 9t = 88, t = 12 – o, substituting as 6o + 9(12 – o) = 88, 6o + 108 – 9o = 88,
108 – 88 = 3o, 20 = 3o, o = 20/3, So t = 12 – 20/3 = 36 -20/3 = 16/3,
therefore each type of house should the builder build are:
One-bedroom houses – 20/3 and two-bedroom houses – 16/3.

Question 2.
Math on the Spot Doug has 45 coins worth $9.00. The coins are all quarters or dimes. How many of each type of coin does Doug have?
Answer:
Doug has 30 quarters and 15 dimes,

Explanation:
Given Doug has 45 coins worth $9.00. The coins are all quarters or dimes.
Number of each type of coin does Doug have let x = number of quarters, y = number of dimes,
The total number of coins is 45. Therefore, Total number of coins: x + y = 45,
Total amount of the coins is $9. Therefore Total cost of the coins: 0.25x + 0.1y = 9,
Therefore x + y = 45 and 0.25x + 0.1y = 9, solving 0.1x + 0.1y = 4.5, 0.1 y = 4.5 – 0.1x, so substituting
0.25x + 0.1y = 9, 0.25x + (4.5 – 0.1x) = 9, 0.15x = 4.5, x = 4.5 / 0.15, x = 30,
y = 45 – 30 = 15, therefore Doug has 30 quarters and 15 dimes.

Question 3.
An young horse, Alex, is chasing an older horse, Champ. Alex is 60 meters behind Champ. Graph a system of equations to solve the problem. Will Alex catch up to Champ? If so, when? If not, why not?

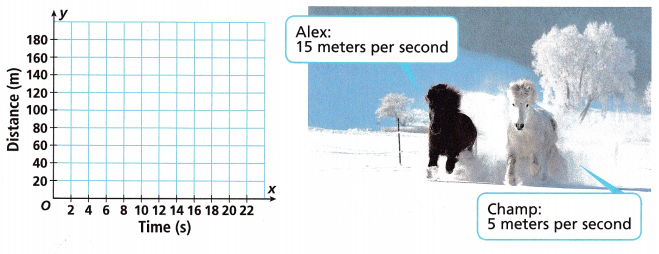
Answer:
System of equations: c = A – 60,

Question 4.
Reason A family owns two cars. One car gets 35 miles per gallon and the other car gets 27 miles per gallon. In one week the family drove a total of 480 miles and used 16 gallons of gas. Can you determine the number of miles the family drove each car? Explain.
Answer:
System of equations: x + y = 16, 35x + 27y = 480,
Number of miles the family drove each car is one car 6 miles and other car 10 miles,

Explanation:
Given a family owns two cars one car gets 35 miles per gallon and the other car gets
27 miles per gallon. In one week the family drove a total of 480 miles and used 16 gallons of gas.
Let one car be x and other car be y so the system of equations are x + y = 16,
35x + 27y = 480, Solving y = 16 – x, 35x + 27(16 – x) = 480, 35x + 432 – 27x = 480,
8x = 480 – 432, 8x = 48, x = 48/8 = 6, therefore number of miles the family drove each car is one car 6 miles and other car 10 miles.

Test Prep

Question 5.
The Greenery landscaping company puts in an order for 2 pine trees and 5 hydrangea bushes for a neighborhood project. The order costs $150. They put in a second order for 3 pine trees and 4 hydrangea bushes that cost $144.50. What is the cost for one pine tree?
$ ____________
Answer:
The cost for one pine tree is $17.5,

Explanation:
Given the greenery landscaping company puts in an order for 2 pine trees and 5 hydrangea
bushes for a neighborhood project. The order costs $150.
They put in a second order for 3 pine trees and 4 hydrangea bushes that cost $144.50.
Let p be oine trees and h be hydrangea bushes, so system of equations are 2p + 5h = 150 and
3p + 4h = 144.50 solving p = (150 -5h)/2, substituting 3(150 – 5h)/2 + 4h = 144.50,
450 – 15h + 8h = 289, 450 – 289 = 7h, 7h = 161, h = 161/7 = 23, now p = 150 – 5 X 23/2 =
p = 150 – 115/2, p = 35/2 or p = 17.5, therefore the cost for one pine tree is $17.5.

Question 6.
Sonia is older than her brother Eddie. The sum of their ages is 38. The difference is 14. How many years old are Sonia and Eddie?
Sonia: years old
Eddie: years old
Answer:
Sonia is 26 years old, Eddie is 12 years old,

Explanation:
Given Sonia is older than her brother Eddie. The sum of their ages is 38.
The difference is 14. Let Sonia be s and Eddie is e, we have s + e = 38 and s – e = 14, solving
s = 38 – e, substituting we get 38 – e – e = 14, 38 – 14 = 2e, 24 = 2e, e = 24/2 = 12,
now s = 38 – 12 = 26, therefore Sonia is 26 years old and Eddie is 12 years old.

Question 7.
The Chenery School sold a total of 78 tickets for the spring concert. Advance tickets sold for $5.00 and tickets purchased the night of the concert cost $10.50. If the total revenue for the night was $533, how many advance tickets were sold?
___________ tickets
Answer:
52 advance tickets were sold,

Explanation:
Given the Chenery School sold a total of 78 tickets for the spring concert. Advance tickets sold for $5.00 and tickets purchased the night of the concert cost $10.50.
The total revenue for the night was $533, Let advance tickets be a and night tickets be n so
a + n = 78, 5a + 10.5n = 533, Solving a = 78 – n,
substituting 5(78 – n) + 10.5n = 533, 390 – 5n + 10.5n = 533,
5.5n = 533 – 390 = 143, n = 143/5.5 = 26, Now a = 78 – 26 = 52, therefore 52 advance tickets were sold.

Check:
5 X 52 + 10.5 X 26 = 260 + 273 = 533 which is true.

Question 8.
Two angles are supplementary. This means that the sum of the two angles is equal to 180°. One of the angles measures 20 degrees more than three times the other angle. What is the measure of the larger angle?
(A) 40°
(B) 120°
(C) 140°
(D) 200°
Answer:
(C) 140°,

Explanation:
Given two angles are supplementary. This means that the sum of the two angles is
equal to 180°. One of the angles measures 20 degrees more than three times the other angle.
Let x be one angle which is smaller angle and y be the other angle which is larger angle as y = 3x + 20° and x + y = 180°, Solving y = 3(180°- y) + 20°, y = 540° – 3y + 20°,
4y = 560°, y = 560°/4 = 140°, so x = 180° – 140° = 40°,
therefore the measure of the larger angle is 140° matches with (C).

Spiral Review

Question 9.
Which two triangles are similar? How do you know?

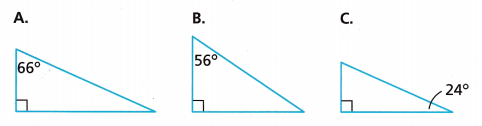
Answer:
Triangles A and C are similar,

Explanation:
Given 3 triangles as we know the sum of angles of right angled triangles is 180° and one angle will be 90°, So triangle A has one angle 90° other angle 66° and another unknown angle is x so x + 90° + 66° = 180°, x = 180° – 156° = 24° which matches with angle of traingle C, therefore triangles A and C are similar.

Question 10.
A line passes through the origin and (4, 6). What are two other points on this line?
Answer:
(2,3) and (2.6,4),

Explanation:
Given a line passes through the origin and (4, 6) the two other points onthis line are we can divide
x and y by 2 we get x = 4/2 = 2 and y = 6/2 = 3, so one point is (2,3) and we divide x and y by 1.5
we get  x = 4/1.5 = 2.666 and y = 6/1.5 = 4 other point is (2.6,4), therefore the two other points on this line are  (2,3) and (2.6,4).

Question 11.
What is an equation of the line with slope -3 through the point (3, 5)?
Answer:
Equation is y = -3x + 14 or 3x + y = 14,

Explanation:
The gradient(slope) y-axis intercept form of a straight line is y = mx +b, where m is the gradient(slope), b is the y-axis intercept we are given a gradient of -3, therefore y = -3x +b,
using the given point (3, 5) to solve for b we have 5 = -3 X 3 + b, b= 5 + 9 = 14, therefore equation is y = -3x + 14 or 3x + y = 14.