We included HMH Into Math Grade 8 Answer Key PDF Module 7 Lesson 1 Represent Systems by Graphing to make students experts in learning maths.
HMH Into Math Grade 8 Module 7 Lesson 1 Answer Key Represent Systems by Graphing
I Can graph a pair of linear equations and draw a conclusion from the graph.

Spark Your Learning
Natasha is comparing two rock climbing gyms in her town. Each gym charges a fixed fee for gear rental (shoes, harness, etc.) and an hourly fee for climbing. The graph shows the total cost at each gym based on the time spent climbing.
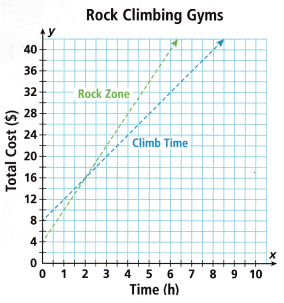

Turn and Talk What information do you get by comparing the y-intercepts of the lines? What information do you get by comparing the slopes of the lines?
Build Understanding
1. Cody is comparing the total costs of two climbing gyms. Each gym charges a fixed fee for gear rental and an hourly fee for climbing. Cody graphs a pair of equations, as shown, to help him compare
the costs.
A. What does the slope represent in this context?
____________________
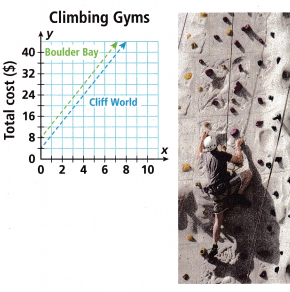
B. How do the slopes of the graphs compare? What does this tell you about the rock climbing gyms?
________________________
C. What does the y-intercept represent in this context?
________________________
D. What do the y-intercepts of the graphs tell you about the rock climbing gyms?
________________________
________________________
________________________
E. What does the difference in the y-intercepts mean in this context?
________________________
F. Which gym is a better deal if Cody plans to climb for 2 hours? if Cody plans to climb for 5 hours? How do you know?
________________________
________________________
G. Is there ever a situation in which Boulder Bay will cost less than Cliff World? Why or why not?
Turn and Talk Suppose Cliff World increases their gear rental fee to $6 but keeps their hourly rate the same. Does this change the answer to any of the Task 1 questions? Explain.
2. A mobile hotspot is a portable device that provides Wi-Fi. Both Cool Connect and Mobile Me offer mobile hotspots for have a total monthly cost of y, which includes a fixed fee plus a charge for the gigabytes (GB) of data you use, x.
A. Graph and label each equation on the coordinate plane.
Given that the equations are
Cool connect y = 0.5x + 7
Mobile me y = 2x + 1
Let us consider x = number of gigabytes.
In cool connect
If x = 1 then y = 0.5(1) + 7 = 7.5
If x = 2 then y = 0.5(2) + 7 = 8
If x = 3 then y = 0.5(3) + 7 = 8.5
If x = 4 then y = 0.5(4) + 7 = 9
Mobile me
If x = 1 then y = 2(1) + 1 = 3
If x = 2 then y = 2(2) + 1 = 5
If x = 3 then y = 2(3) + 1 = 7
If x = 4 then y = 2(4) + 1 = 9
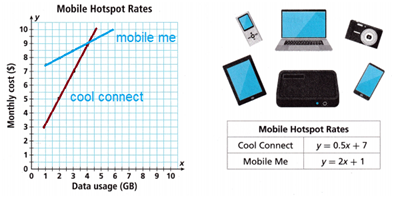
B. What is the slope of each line? What do the slopes tell you?
____________________
____________________
____________________
____________________
Answer:
Given that the equations are
Cool connect y = 0.5x + 7
Mobile me y = 2x + 1
The equations are in the form of y = mx + c
m = slope and c = y intercept.
The slope of the Cool connect is 0.5
The slope of the Mobile Me is 2.
C. What is the y-intercept of each line? What do the y-intercepts tell you?
____________________
____________________
Answer:
Given that the equations are
Cool connect y = 0.5x + 7
Mobile me y = 2x + 1
The equations are in the form of y = mx + c
m = slope and c = y intercept.
The y intercept of the Cool connect is 7
The y intercept of the mobile me is 1.
Y intercept tells the monthly cost.
D. What does the point of intersection of the lines represent?
____________________
____________________
Answer:
It the intersection point monthly cost for gigabytes is the same.
E. When does one mobile hotspot cost less than the other? Explain your thinking.
____________________
____________________
____________________
____________________
Answer:
Given that the equations are
Cool connect y = 0.5x + 7
Mobile me y = 2x + 1
Let us consider x = number of gigabytes.
In cool connect
If x = 1 then y = 0.5(1) + 7 = 7.5
Mobile me
If x = 1 then y = 2(1) + 1 = 3
For Cool connect 1 giga bytes for 1 month is 7.5
For Mobile me 1 giga bytes for 1 month is 3
The mobile hotspot for mobile me is less than the mobile me.
3. Two shops that rent snorkeling equipment have their pricing information shown. Each store charges a fixed fee for gear rental (snorkel, mask, fins) and an hourly rate. The total cost y for renting equipment for x hours at The Sea Shack is given by the equation y = 2x + 3. The total cost for Water Town is given in the table.
A. Graph and label each equation on the coordinate plane.
__________________________
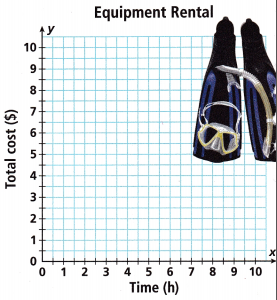
Answer:
Given that,
The equation for the sea shack is y = 2x + 3
If x = 1 then y = 2(1) + 3 = 5
If x = 2 then y = 2(2) + 3 = 7
If x = 3 then y = 2(3) + 3 = 9
The points of the water town is (1,5), (2,7) (3,9)
Both the sea shack and the water town as the same coordinates.
B. What do you notice about the graphs?
__________________________
Answer:
From the graph
The sea shack and the water town as the same total cost.
C. What do the y-intercepts and the slopes tell you?
__________________________
__________________________
__________________________
Answer:
The slop of the sea shack and the water town is 2
The y intercept of the sea shack and the water town is 3.
D. Which shop is the better deal? Explain.
__________________________
__________________________
Check Understanding
Use the information to solve Problems 1—4.
Jovan is considering two job offers. Each company pays a fixed monthly salary plus a commission based on the amount of sales. The graph shows the income potential for each job.
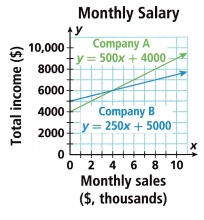
Question 1.
Which company pays a greater monthly salary? Explain.
Answer:
Given that,
The monthly salary of company A is y = 500x + 4000.
The monthly salary of Company B is y = 250x + 5000.
Here 500x and 250 are the salaries of Company A and company B.
The 4000 and 5000 are the commission.
Company A has a greater salary.
Question 2.
Which company pays a greater commission? Explain.
Answer:
Given that,
The monthly salary of company A is y = 500x + 4000.
The monthly salary of Company B is y = 250x + 5000.
Here 500x and 250 are the salaries of Company A and company B.
The 4000 and 5000 are the commission.
Company B has the greater commission.
Question 3.
If Jovan plans to have monthly sales of $5000, which job pays more?
Answer:
Given that,
The monthly salary of company A is y = 500x + 4000.
The monthly salary of Company B is y = 250x + 5000.
Here x = number of sales.
The number of sales = 5000.
The monthly salary of company A is y = 500(5000) + 4000.
= 2,504,000
The monthly salary of Company B is y = 250(5000) + 5000.
= 1,255,00
Therefore company A jobs pay more.
Question 4.
For what value of monthly sales do the two companies pay the same total income?
Answer:
Given that,
The monthly salary of company A is y = 500x + 4000.
The monthly salary of Company B is y = 250x + 5000.
If the company A has the number of sales x = 5 then
The monthly salary of company A is y = 500(5) + 4000.
= 6500.
If the company A has the number of sales x = 6 then
The monthly salary of Company B is y = 250(6) + 5000.
= 6500.
For company A the x value is 5 and For company B the x value is 6 For these values both companies have the same monthly income.
On Your Own
Use the graph comparing the cost of two ice skating rinks to answer Problems 5—7. Each rink charges a fixed fee for skate rentals and an hourly fee for skating.
Question 5.
Compare the slopes of the lines. What do they tell you in this context?
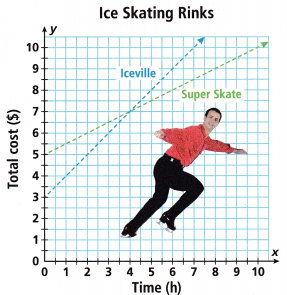
Answer:
The formula for the slop of the graph = change in y/change in x
The change in x for Iceville is x = 3
The Change in y for the Iceville y = 3
The slope of the Iceville = change in y/change in x = 3/3 = 1
The change in x for Super Skate is x = 3.5
The Change in y for the Super skate is y = 2
The slope of the Super skate = change in y/change in x = 2/3.5 = 0.57
The slope of Iceville is greater than the slope of Super skate.
Question 6.
Compare the y-intercepts of the graphs. What does this tell you in this context?
Answer:
The formula for the y-intercept is y = mx + c
m = slope.
The slope of the Iceville = 1
The slope of the Super skate = 0.57
The y-intercept of the Iceville is y = x + c
The y-intercept of the Super skate is y = 0.57x + c
Question 7.
Financial Literacy Under what circumstances does Super Skate charge less? Explain.
Answer:
Use the graph comparing two phone plans to answer Problems 8—10. Each plan includes a fixed monthly fee, plus a fee based on the number of hours used.
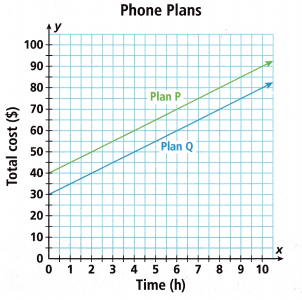
Question 8.
Compare the slopes of the lines. What do they tell you in this context?
Answer:
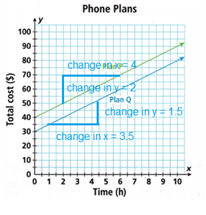
The formula for the slop of the graph = change in y/change in x
The slope of green line is = 2/4 = ½ = 0.5.
The slope of blue line is 1.5/3.5 = 0.42
The slope of green line greater than the blue line.
Question 9.
Compare the y-intercepts of the lines. What do they tell you in this context?
Answer:
The formula for the y intercept is y = mx + c
m = slope.
The slope of green line is = 2/4 = ½ = 0.5.
The slope of blue line is 1.5/3.5 = 0.42
The y intercept of the green line is y = 0.5x + c
The y intercept of the blue line is y = 0.42x + c
Question 10.
Financial Literacy Which plan offers a better deal? Does it depend on how long Suki expects to talk on the phone?
Answer:
Question 11.
There are two taxi companies in Kara’s town. The total cost y for a ride based on distance driven x (in miles) for XYZ Taxi is given by the equation y = 0.5x + 4. The total cost for Quick Ride is given in the table.
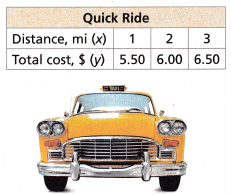
A. Graph and label the equation representing XYZ Taxi. Graph the data from the table for Quick Ride onto the coordinate plane and connect the points with a line.
Answer:
Given that,
The equation of the XYZ Taxi is y = 0.5x + 4.
The total cost = y
The distance driven = x
If x = 1 then y = 0.5(1) + 4 = 4.5
If x = 2 then y = 0.5(2) + 4 = 5
If x = 3 then y = 0.5(3) + 4 = 5.5
If x = 4 then y = 0.5(4) + 4 = 6
The coordinates of Quick Ride is (1, 5.50), (2, 6), (3,6.50)
The equation of Quick Ride is y = 0.5x + 5
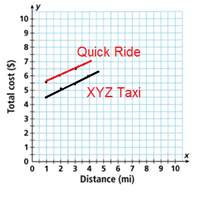
B. Calculate, compare, and interpret the slopes and the y-intercepts.
____________________
Answer:
Given that,
The equation of the XYZ Taxi is y = 0.5x + 4.
The equation of Quick Ride is y = 0.5x + 5
The cost of 1 mile for the XYZ Taxi is 4.5
The cost of 1 mile for the Quick ride is 5.5
The slop of the XYZ Taxi and Quick Ride is 0.5
The y intercept of the XYZ taxi is 4.
The y intercept of the Quick Ride is 5.
The XYZ Taxi and the Quick Ride is not intercepted.
The cost of 1 mile of XYZ Taxi is less than the Quick ride.
C. Reason What can you conclude from your graph?
____________________
Answer:
From the graph
The cost of 1 mile of XYZ Taxi is less than the Quick ride.
Question 12.
Use Structure The total cost in dollars y of a bus pass for x months in City A is given by y = 30x + 5. The total cost in City B is given by y = 30x + 4.5. After graphing both equations on your own paper, which city offers a better deal? How do you know?
Answer:
Question 13.
Mitchell is comparing the cost of frozen yogurt at two different shops. He makes a graph relating the number of ounces of yogurt on the x-axis to the cost of the yogurt on the y-axis. The graph for each shop is a straight line and the lines intersect at (4, 3.25). What can you conclude from this?
Answer:
I’m in a Learning Mindset!
How do I know if representing multiple equations is an appropriate challenge for me?
Lesson 7.1 More Practice/Homework
Use the graph comparing the cost of two laundry services to answer Problems 1—3. Each service charges a fixed fee and a price per pound of laundry.
Question 1.
Compare the slopes. What does this tell you?
Answer:
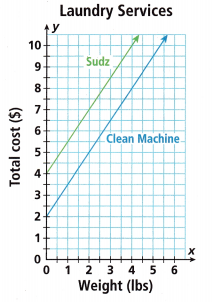
Question 2.
Compare the y-intercepts. What does this tell you?
Answer:
Question 3.
Financial Literacy Which service offers a lower total price? Explain.
Answer:
Question 4.
Compare the costs of two tablet computers. In addition to the cost of the tablet, there is a monthly data fee.
A. Graph and label the equations on the coordinate plane shown.
Answer:

Given that the equations are
Brand A = y = 50x + 100
Brand B = y = 25x + 200
Let us consider number of months = x
In Brand A
If x = 1 then y = 50(1) + 100 = 150
If x = 2 then y = 50(2) + 100 = 200
If x = 4 then y = 50(4) + 100 = 300
If x = 8 then y = 50(8) + 100 = 500
In Brand B
If x = 1 then y = 25(1) + 200 = 225
If x = 2 then y = 25(2) + 200 = 250
If x = 4 then y = 25(4) + 200 = 300
If x = 8 then y = 25(8) + 200 = 400
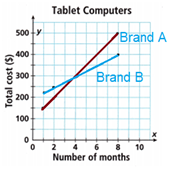
B. Financial Literacy Which tablet has a lower monthly data fee? Explain.
Answer:
Brand A monthly fee = 150
Brand B monthly fee = 225
The Brand A monthly fee is lower.
C. Construct Arguments If the plan is to use the tablet for eight months, which tablet costs less overall? Explain.
___________________
___________________
___________________
Answer:
Given that the equations are
Brand A = y = 50x + 100
Brand B = y = 25x + 200
Let us consider number of months = x
For Brand A
If x = 8 then y = 50(8) + 100 = 500
For Brand B
If x = 8 then y = 25(8) + 200 = 400
For eight months the Brand B fee is less than The Brand A.
Test Prep
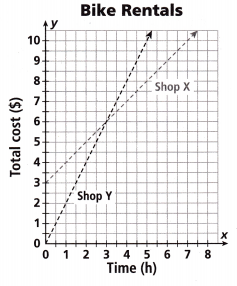
Use the graph to answer Problems 5-6.
Question 5.
Based on the graph, which of the following is true?
A. For a 1-hour rental, Shop X is a better deal.
B. For a 6-hour rental, both shops have the same cost.
C. Shop Y is a better deal for any number of hours.
D. It costs $6 to rent a bike for 3 hours at either shop.
Answer:
In the given graph the shop x and the shop y are intersecting at the point (3, 6).
So, it costs $6 to rent a bike for 3 hours at either shop.
Option D is the correct answer.
Question 6.
If you plan to rent a bike for 5 hours, how much do you save by choosing Shop X rather than Shop Y?
A. $0.50
B. $1.00
C. $2.00
D. $2.50
Answer:
Time = 5 hours
The total cost of shop Y is $10
The total cost of shop X is $8
10 – 8 = $2
Thus option C is the correct answer.
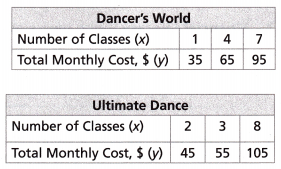
Question 7.
There are two dance studios. The tables show the total monthly cost y for each studio based on the number of classes taken that month x. Graph the data from each table on your own paper and connect the points with a line. What can you conclude from your graph?
Answer:
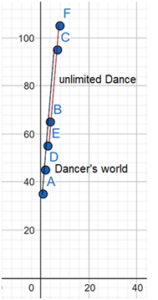
In both the classes the total monthly cost is increased by 10 when the classes are increased by 1.
Spiral Review
Question 8.
Can you conclude from the figure that ∆ABC is similar to ∆DEF? Explain.
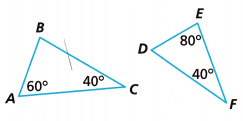
Answer:
Some of the angles in the triangle = 180 degrees
In triangle ABC.
angle A + angle B + angel C = 180 degrees.
60 degrees + 40 degrees + angle C = 180 degrees
100 degrees + angle C = 180 degrees.
Angle C = 180 – 100 = 80 degrees.
In triangle DEF
angle D + angle E + angel F = 180 degrees.
60 degrees + 40 degrees + angle D = 180 degrees
100 degrees + angle D = 180 degrees.
Angle D = 180 – 100 = 80 degrees.
Therefore that ∆ABC is similar to ∆DEF.
Question 9.
In the figure, ∠Q is congruent to ∠T, and ∠R is congruent to ∠U. What are the measures of ∠P and ∠S?
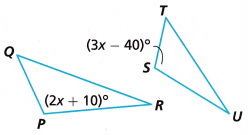
Answer:
2x + 10 = 3x – 40
10 + 40 = 3x – 2x
x = 50
So, the measures of ∠P and ∠S = 50°
For Problems 10-11, tell whether each equation has no solution or infinitely many solutions.
Question 10.
3(x+ 2) = x + 2x + 2
Answer:
Given that,
3(x+ 2) = x + 2x + 2
3x + 6 = x + 2x + 2
3x + 6 = 3x + 2
Subtract 6 from both sides
3x + 6 – 6 = 3x + 2 – 6
3x = 3x -4
Subtract 3x from both sides
3x – 3x = 3x -4 – 3x
0 = -4
Therefore the equation has no solution.
Question 11.
1.5y + y + 10 = 2.5(y + 4)
Answer:
Given that,
1.5y + y + 10 = 2.5(y + 4)
2.5y + 10 = 2.5y + 10
Subtract 10 from both sides
2.5y + 10 – 10 = 2.5y + 10 – 10
2.5y = 2.5y
Subtract 2.5y on both sides
2.5y – 2.5y = 2.5y – 2.5y
0=0
Therefore the equation has no solution.