We included HMH Into Math Grade 8 Answer Key PDF Module 6 Lesson 4 Construct Functions to make students experts in learning maths.
HMH Into Math Grade 8 Module 6 Lesson 4 Answer Key Construct Functions
I Can construct functions based on verbal descriptions, tables, and graphs.
Spark Your Learning
A scuba diver descends from the surface of the ocean at a constant rate of 5 feet per minute to a maximum depth of 130 feet. The diver’s depth in feet y is a function of the number of minutes x since the diver began descending. What do you know about the function?


Turn and Talk Consider a function where x represents a number of people. Is this function discrete or continuous? What must be true of all x-values? Explain.
Build Understanding
1. The parking lot near the scuba company opens for the day at 6:00 a.m. Between 7:00 a.m. and 11:00 a.m., cars park at a constant rate of 50 per hour. At 10:00 a.m., 165 cars are parked in the lot. Write an equation that represents the situation in the form y = mx + b.

A. Write the ordered pair that represents 165 cars parked at 10:00 a.m. What does each coordinate of the point represent?
___________________
___________________
___________________
B. What is the slope of the function? Use the slope and the point from Part A to find the y-intercept and write the equation of the line.
___________________
C. Can time be a fractional number? Why or why not?
__________________
D. Can the number of cars be a fractional number? Explain.
__________________
E. Is this function discrete or continuous? Why?
__________________
__________________
F. What are some restrictions for the possible values of y? Why?
__________________
__________________
__________________
G. What are some restrictions for the possible values of x?
__________________
H. What does the y-intercept of the function represent in this equation?
__________________
Step It Out
2. A factory produces mobile phones at a constant rate. The table shows four ordered pairs whose points exist on the graph of the function representing the factory’s output. In the ordered pairs, x is the number of shifts worked and y is the number of mobile phones produced. Write the equation of the linear function that includes these points in the form y = mx + b.

A. Complete the sentence to describe how to find the slope of the graph of the function.
Find the change in ![]() -values divided by the change in
-values divided by the change in ![]() -values.
-values.
Answer:
The change in y values is divided by the change in x values.
B. Any two given points can be used to find the slope of the line. Use (2, 240) and (5, 600) to find the slope of the line.
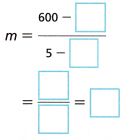

Answer:
Given points are (2, 240), (5,600)
slope = m = y2 – y1/x2 – x1.
m = (600-240)/(5-2)
m = 360/3 = 120
C. Use the x- and y-values from (2, 240) and the slope from Part B to solve for the y-intercept b.
240 = ![]() (2) + b
(2) + b
![]() =
= ![]() + b
+ b
b = ![]()
Answer:
Given that,
x and y values are (2, 240)
Slope = 120
240 = 120(2) + b
240 = 240 + b
240 – 240 = b
0 = b
D. Write the equation of the line.
_______________________
Answer: The equation of the line is y = 120x
E. is this function discrete or continuous? Explain.
_______________________
_______________________
F. Are there any restrictions on the domain or range values? Explain.
_______________________
_______________________
Turn and Talk Why does it make sense for the function to have a y-intercept of 0?
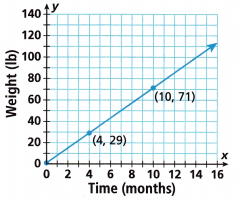
3. The following graph shows the weight of a newborn giant panda from birth to 16 months of age. Write the linear function in the form y = mx + b.
B. Use the x- and y-values from any point to solve for the y-intercept b.
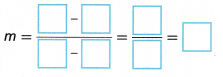
C. write the equation of the line.

Answer:
Given that the coordinates points are
(x1, y1) = (4, 29)
(x2, y2) = (10, 71)
The equation of the line is in the form of y = mx + b
Slope = m = y2 – y1/x2 – x1
= 71 – 29/ 10 – 4
= 42/6
Slope = 7
y-intercept b = y – mx
b = 29 – 7(4)
y intercept b = 1
The equation of the line is y = 7x + 1
Check Understanding
Question 1.
Write a linear function with a slope of 4 that includes the point (-1, 3).
Answer:
The equation of the line is in the form of y = mx + b
Points (x, y) = (-1, 3)
Slope = 4
b = y – mx
= 3 – 4(-1)
= 3 + 4
= 7
The linear function is y = 4x + 7
Question 2.
Write a function for the line that includes the points (4, -5) and (8, -7).
Answer:
The equation of the line is in the form of y = mx + b
The points are (x1, y1) = (4, -5)
(x2, y2) = (8, -7)
Slope = m = y2 – y1/ x2 – x1
= -7 – (-5)/ 8 – 4
= -2/4
m = -1/2
b = y – mx
b = – 5 – (-1/2) (4)
= -5 – (-2)
= – 5 + 2
b = -3
Therefore the function for the line is y = -1/2x – 3.
Question 3.
Sullivan is filling a swimming pool and graphs the amount of water in the pool as a function over time. Explain whether the function is discrete or continuous.
Answer:
It is a continuous function. Because both the time and the water in the pool are continuously increasing.
On Your Own
Use the graph and information to answer Problems 4-9.
Bridget has 13 gallons of gasoline to use for her lawn-mowing business. She uses gasoline in the lawn mower at a constant rate. Let x represent the number of lawns mowed and y represent the 10 amount of gasoline remaining. Look at the graph of this function. Construct the function for this scenario.
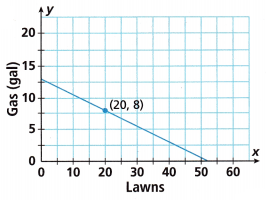
Question 4.
Model with Mathematics What is the equation of the line?
Answer:
Given that,
Bridget has 13 gallons of gasoline.
The remaining gasoline = 10.
(x1, y1) = (13, 10)
(x2, y2) = (20, 8)
The equation of the line is in the form of y = mx + b
Slope = m = y2 – y1/x2 – x1
= 8 – 10/20 – 13
Slope = -2/7
b = y – mx
= 10 – (-2/7) (13)
= 10 + 3.71
b = 13.71
The equation of the line is y = -2/7x + 13.71
Question 5.
What is the initial value of the function and what does it represent?
Answer:
Initial value = y-intercept = b
The initial value is 13.71. It represents the remaining gasoline.

Question 6.
What is the slope and what does it mean?
Answer: The slope of the equation is -2/7. It represents the difference between gas and lawns.
Question 7.
Reason Is the function discrete or continuous? Why?
Answer: It is a discrete function because the gas and the lawns are continuously decreasing.
Question 8.
Attend to Precision What Is the domain? Explain any restrictions.
Answer: Domain restrictions allow us to create functions defined over numbers that work for our purposes. If the function is a rational function and the denominator is 0 for some value or values of x
Question 9.
Attend to Precision What Is the range? Explain any restrictions.
Answer: A restricted range is a range of values that have been condensed, or shortened. the range of the function is the set of all values that f takes.
Question 10.
Model with Mathematics Sabrina collects trading cards. She buys packages of 12 trading cards to add to her collection. After she adds 16 packages to her existing collection, she has a total of 274 cards. Write a function to model the size of Sabrina’s collection.
Answer:
Given,
She buys packages of 12 trading cards to add to her collection.
After she adds 16 packages to her existing collection, she has a total of 274 cards.
Each package = 12
x + (12 × 16) = 274
x + 192 = 274
x = 274 – 192
x = 82

Question 11.
Construct a linear function that represents the table of values shown.
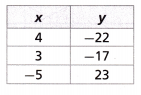
Answer:
From the table the equation is y = – 4x – 2.
If x = 4 then y = -5(4) – 2 = 22
If x = 3 then y = -5(3) – 2 = -17
If x = -5 then y = -5(-5) – 2 = 23
The linear function that represents the table is -4x – 2.
Question 12.
Write a function representing the line that includes the points (3, 3) and (-6, 15).
Answer:
Given that,
The points are (x1, y1) = (3, 3)
(x2, y2) = (-6, 15)
The equation of the line is in the form of y = mx + b
Slope = m = y2 – y1/x2 – x1
= 15 – 3/-6 – 3
= 12/-9
Slope = 4/-3
b = y – mx
= 3 – (-4/3) (3)
= 3 + 4
b = 7
The function representing the line is y = -4/3x + 7
Question 13.
Write a linear function for the line with a slope of -5 that passes through the point (7, 3).
Answer:
Given that,
The slope = -5
The points = (7, 3)
The linear equation of the line is in the form of y = mx + b
3 = -5(7) + b
3 = -35 + b
b = 35 + 3
b = 38
Therefore the linear function of the line is y = -5x + 38.
Question 14.
Reason If you know one point on the graph of a line, what other piece of information do you need in order to construct the function representing that line in the form y = mx + b? Explain.
Answer:
The one point on the graph of the line means it is (x, y) points.
We need the other piece of information to construct the function y = mx + b. Because to find the slope we need two points.
One point is not enough to construct the function y = mx + b
Question 15.
Open Ended The graph of a function passes through the point (2, 18). Choose another point on the graph and write the linear function representing those two points in the form y = mx + b.
Answer:
Given that the points are (2, 18)
You can choose another point on the graph is (3, 20)
The equation is in the form of y = mx + b
Slope = m = y2 – y1/ x2 – x1
= 20 – 18/ 3 – 2
= 2/1
Slope = 2
b = y – mx
b = 18 – 2(2)
= 18 – 4
b = 14
The linear function representing the two points is y = 2x + 14.
I’m in a Learning Mindset!
How can writing a linear function given points be a challenge? Is it still a challenge?
Lesson 6.4 More Practice/Homework
Question 1.
Model with Mathematics Cassidy is selling popcorn for a fundraiser sale at the price shown. He purchases a total of 150 containers of popcorn to sell. After he sells 15 containers, he will make a total profit, after his upfront costs, of $5.50. Cassidy’s profit, after upfront costs, can be modeled by a linear function in the form y = mx + b.
A. What is the slope of the line that models the function?
______________________

B. How much were Cassidy’s upfront costs?
______________________
C. Will the function be discrete or continuous? Explain.
______________________
D. Write the function that models Cassidy’s profit.
______________________
E. What is the domain of the function?
______________________
F. What is Cassidy’s profit or loss if he does not sell any popcorn?
______________________
G. What is Cassidy’s profit if he sells all of the popcorn?
______________________
H. What is the range of the function?
______________________
Answer:
The domain and the range of the function describe the possible profit or loss from the sale of popcorn and the number of popcorn units.
Given that the number of containers sole is countable, the function will be discrete.
Cost of containers = Revenue – Profit
Cost of the containers = 1.5 × 25 – 5.5 = 32
y = 1.5x – 32
The domain is the 150 containers
domain = 0 ≤ x ≤ 150
When no popcorn is sold, we have;
x = 0, which gives;
y = 1.5 × 0 – 32 = -32
If he does not sell any popcorn, the loss is $32
If all the popcorn are sold, we have
x = 150
y = 1.5 × 150 – 32 = 193
The profit if all the popcorn are sold = $193
The range of the function are the possible y values, which is the possible profit or loss
Range = -32 ≤ y ≤ 193
For Problems 2-3, write a function for the line with the given slope that passes through the point.
Question 2.
passes through the point (4, 5); slope = –\(\frac{1}{4}\)
Answer:
Given that the points are (4, 5)
The slope is -1/4
The function of the line is in the form of f(x) = mx + b
b = f(x) – mx
b = 5 – (-1/4) (4)
b = 5 + 1
b = 6
The function of the line is f(x) = -1/4x + 6
Question 3.
contains the point (2, 1); slope = 5
Answer:
The function of the line is f(x) = mx + b
Slope = m
(x, y) = (2,1)
Slope = 5
b = f(x) – mx
= 1 – 5(2)
= 1- 10
b = -9
Therefore the function of the line is f(x) = 5x – 9.
Question 4.
Math on the Spot Write the equation of the line that passes through (-3, 1) and (2, -1) in slope-Intercept form.
Answer:
Given that the points are
(x1, y1) = (-3, 1)
(x2, y2) = (2, -1)
The equation of the line is in the form of y = mx +c
Slope = m = -1-1/2 -(-3)
= -2/5
= -2/5
c = y – mx
c = 1 – (-2/5) (-3)
c = -1/5
The equation of the line is y = 2/5x -1/5.
Test Prep
Question 5.
Complete the equation of the line that passes through (-2, 6) and (-1, 18) in slope-intercept form.
y = ![]() x +
x + ![]()
Answer:
Given that the points are
(x1, y1) = (-2, 6)
(x2, y2) = (-1, 18)
The equation of the line is in the form of y = mx +c
Slope = m = 18 – 6/-1-(-2)
= 16/1
= 16.
c = y – mx
c = 6 – 16(-2)
= 6 + 32
y intercept = c = 38
The equation of the line is y = 16x + 38.
Question 6.
The cost c to rent a car for d days is shown in the table. Which equation represents this function?
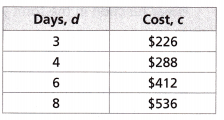
A. c = 75.3d
B. c = 72d – 40
C. c = 67d
D. c = 62d + 40
Answer:
Given that c = 75.3d
If d = 3 then c = 75.3(3) = 225.9
c = 72d – 40
If d = 3 then c = 72(3) – 40 = 176
c = 67d
If d = 3 then c = 67(3) = 201
c = 62d + 40
If d = 3 then c = 62(3) + 40 = 226
Option A is the correct answer.
Question 7.
Choose the function that represents the graph on the coordinate plane.
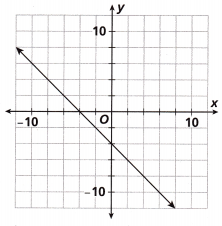
A. y = -4x
B. y = -4x – 4
C. y = -x – 4
D. y = -x + 4
Answer:
The coordinate points from the graph is (-2, 0) and (0, -2)
We know that the equation of the line is y = mx + c
Slope = m = y2 – y1/x2 – x1
= -2-0/0 – (-2)
= -2/2
= -1.
c = y – mx
c = -2 – (-1) (-2)
c = -2 – 2
c = -4
The equation of the line is y = -x – 4.
Option C is the correct answer.
Question 8.
The graph of a function has a slope of -6, passes through the point (-3, 4), and is a straight line. Choose all the statements that must be true.
A. The graph will pass through the point (1, 20).
B. The graph will pass through the point (-1, 8).
C. The graph represents a discrete function.
D. The function has a y-intercept at (0, -14).
Ë. The constant rate of change is -6.
Answer:
Question 9.
Is a function that can be graphed as a solid line discrete or continuous?
Answer: Discrete functions have to scatter plots as graphs and continuous functions have lines or curves as graphs. If a continuous function has a graph with a straight line, then it is referred to as a linear function
Spiral Review
Question 10.
Solve for x: 7x – 14 = 14 – 7x.
Answer:
Given that the equation is
7x – 14 = 14 – 7x.
7x – 14 – 14 + 7x = 0
14x – 28 = 0
14x = 28
x = 28/14
x = 2
Question 11.
Complete the table representing a linear function.
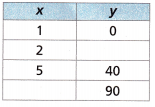
Answer: