Into Math Grade 8 Module 6 Lesson 2 Answer Key Derive and Interpret y = mx + b

We included HMH Into Math Grade 8 Answer Key PDF Module 6 Lesson 2 Derive and Interpret y = mx + b to make students experts in learning maths.

HMH Into Math Grade 8 Module 6 Lesson 2 Answer Key Derive and Interpret y = mx + b

I Can derive the equation for a line in the form y = mx + b given the slope of the line and a point.

Spark Your Learning

Based on data from a science experiment, Sierra graphs Lines A, B, and C. Compare the lines. How are the graphs the same? How are the graphs different?

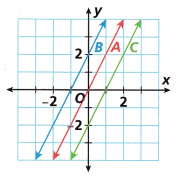
Turn and Talk What would be the equation of a line that passes through the origin and the point (1, -2)? Explain.

Build Understanding

1. The y-intercept of a graph is the y-coordinate of the point where the graph crosses the y-axis, or the value of y when x equals 0. A line that passes through the origin can be represented by an equation of the form y = mx.
A. Consider a line with slope m and y-intercept b. Write the ordered pair that represents the y-intercept.
______________________
B. Recall that slope is rise over run, or the ratio of change in y to change in x. Complete the equation for the slope m of the line using the point from Part A and another point on the line (x, y).

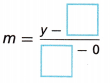
C. Solve the equation from Part B for y.

The y = mx + b form of the equation of a line is called slope-intercept form.
D. Identify the slope and y-intercept of each graph.

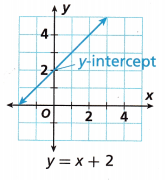
slope: ____
y-intercept: ____
Answer:
Given that the equation is y = x + 2
The equation is in the form of y = mx + c
The slope = 1
y-intercept = 2

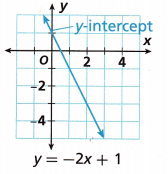
slope: ____
y-intercept: ___
Answer:
Given that the equation is y = -2x + 1
The equation is in the form of y = mx + c
The slope = -2
y-intercept = 1

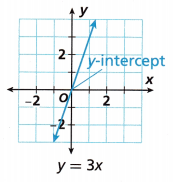
slope: ____
y-intercept: ____
Answer:
Given that the equation is y = 3x + 0
The equation is in the form of y = mx + c
The slope = 3
y-intercept = 0

E. How do the coefficient m of x and the constant b in each equation relate to the slope and y-intercept?
Answer: When the linear function is solved for y then the coefficient of x is the slope and the constant b is the y-intercept.

Step It Out

2. A. Is the slope of Line A positive or negative? Is the slope of Line B positive or negative?
________________
B. Find the slope of each line.
Line A: Line B:

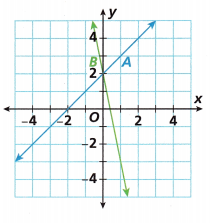
C. What are the y-intercepts of the lines?
_____________________
D. Write the equation of Line A in slope-intercept form.
y = x +
E. Write the equation of Line B in slope-intercept form.
y = x +

3. A line has a slope m = -1. One point on the line is (2, 4). Substitute the x, y, and m values into the slope-intercept form of an equation to find the y-intercept. Then write the equation of the line in slope-intercept form.

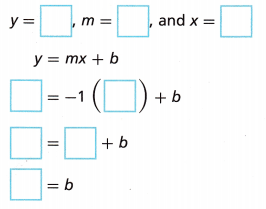
The y-intercept is ____.
The equation of the line is y = x + .
Answer:
Given that,
y = 4, m = -1, x = 2
The equation of the line is y= mx + b
4 = -1(2) + b
4 = -2= b
b = 4 + 2
b = 6
The y-intercept is 6
The equation of the line is y = -1x + 6.

Turn and Talk Will the graph of y = 3x – 3 pass through the origin? If so, how do you know? If not what is the y-intercept?

Linear functions contain only points that lie on a straight line. Some examples of nonlinear functions are:
yx = 5 y = \(\frac{2}{x}\) y = x² + 2

Connect to Vocabulary
The equation of any line can be written in the form y = mx + b. The graphs of functions whose equations cannot be put into this form are not straight lines. Such functions are called nonlinear functions.

4. Solve each equation for y. Then determine whether the function is linear or nonlinear.
A. 5y = 13x – 9
_______________
Given that the equation is 5y = 13x -9
y = 13x – 9/5.
If x = 1 then y = 13(1) – 9/5 = 0.8
If x = 2 then y = 13(2) – 9/5 = 3.4
If x = 3 then y = 13(3) – 9/5 = 6
Therefore the given equation is linear. Because the x and y are continuously increasing.
B. \(\frac{y}{6}\) = 1
_______________
C. xy = 25
_______________
Answer:
Given that the equation is xy = 25
y = 25/x
If x = 1 then y = 25/1 = 25.
If x = 2 then y= 25/2 = 12.5
If x = 3 then y = 25/3 = 8.33
Therefore the given equation is nonlinear. Because the x value increases then the y value decreases.

Nonlinear functions contain points that do not lie on a straight line with the other points. For example, the formula for the area of a square. A = s², is nonlinear because it contains the points
(1, 1), (3, 9), and (4, 16), which do not all lie on a straight line.

5. Graph three points for each equation on your own paper. Is the equation linear or nonlinear? List the 3 points you used.

A. \(\frac{7}{2}\) = x – y
_________________
Answer:

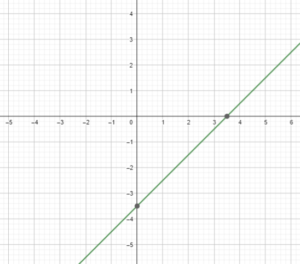
It is linear graph.

B. y = x² + x + 1
_________________
Answer:

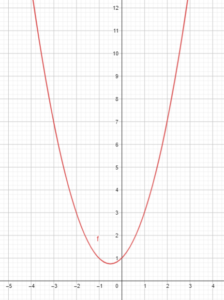
It is not a linear equation.

C. y – 3 = \(\frac{5 x}{2}\)
_________________
Answer:

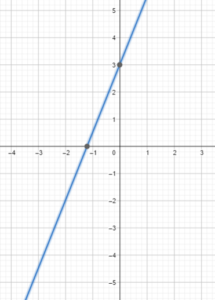
It is a linear equation.

Check Understanding

Question 1.
The slope of a line is -3, and a point on the line is (4, -1). Can the equation of the line be expressed in slope-intercept form? If so, what is the equation? Does the line pass through the origin? How do you know?
Answer:
Given that,
The slope of the line is -3
The point of the line is (4, -1)
The equation of the line is y = mx + b
-1 = -3(4) + b
-1 = -12 + b
-1 + 12 = b
b = 11
Therefore the equation of the line is y = -3x + 11
If x = -1 then y = -3(-1) + 11 = 14
If x = 0 then y = -3(0) + 11 = 11
If x = 1 then y = -3(1) + 11 = 8
The equation does not passes through the origin, because no one point is (0, 0).

Question 2.
Is the graph of y = x² + 2 a straight line? Explain.
Answer:
Given that
The equation is y = x² + 2
If x = 0 then y = 0² + 2 = 2
If x = 1 then y = 1² + 2 = 3
If x = 2 then y = 2² + 2 = 6
Here x increases y increases, so the given equation is straight line.

On Your Own

Use the information to answer Problems 3-4.

Abha is climbing a mountain. While covering 20 yards of horizontal distance, Abha’s elevation increases by 40 yards. Consider Abha’s climb as a linear function.

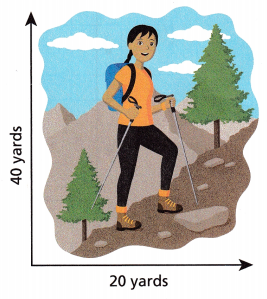
Question 3.
What is the slope of her climb?
Answer:
Given that,
Abha is climbing a mountain.
She is covering 20 yards in horizontal distance.
Abha’s elevation is increased by 40 yards.
The slope of the climb = 40 yards/20 yards = 2.
The slope of her climb is 2.

Question 4.
When would the slope of Abha’s climb be negative?
Answer:

Question 5.
Does the line 54y = 13x pass through the origin? How do you know?
Answer:
Given equation is 54y = 13x
y = 13/54x
y = 0.24x
If x = -1 then y = 0.24(-1) = -0.24
If x = 0 then y = 0.24(0) = 0
If x = 1 then y = 0.24(1) = 0.24
The points are (-1, -0.24), (0, 0), (1, 0.24).
The equation is pass through the origin. Because the x and y values are 0.

Question 6.
Daliyah is given one point on a line as (3, -1) and the slope of the line as -5.

A. What is the y-intercept of the line?
Answer:
The equation of the line is in the form of y = mx + b
The point is (3, -1)
The slope is -5.
-1 = -5(3) + b
-1 = -15 + b
-1 + 15 = b
14 = b
The line of equation is y = -5x + 14
The y-intercept is 14.

B. Write the equation of the line.
Answer:
The equation of the line is in the form of y = mx + b
The point is (3, -1)
The slope is -5.
-1 = -5(3) + b
-1 = -15 + b
-1 + 15 = b
14 = b
The line of equation is y = -5x + 14

Question 7.
Open Ended Write one linear and one nonlinear equation.
Answer:
The linear equation is y = 1.5x + 2.
The nonlinear equation is y = 3x + 2.

For Problems 8—9, write the equation in slope-intercept form, identify the sign of the slope, and state whether the line passes through the origin.

Question 8.
2y – 3x = 4
Answer:
Given that
2y – 3x = 4
The slope-intercept form of the line is y = mx + b
2y = 3x + 4
y = 3x + 4/2
y = 1.5x + 2
The equation of the line is y = 1.5x + 2
The sign of the slope is positive.
If x = -1 then y = 1.5(-1) + 2 = 0.5
If x = 0 then y = 1.5(0) + 2 = 2
If x = 1 then y = 1.5(1) + 2 = 3.5
The points are (-1, 0.5), (0, 2), (1, 3.5).
If both the x and y points are 0 then the line passes through the origin.
The given equation is not pass through the origin.

Question 9.
-5 = -y – 3x
Answer:
The slope-intercept form of the line is y = mx + b
The equation is
-5 = -y – 3x
-5 + y = -3x
y = -3x + 5
The slope of the equation is negative.
If x = -1 then y = -3(-1) + 5 = 8
If x = 0 then y = -3(0) + 5 = 5
If x = 1 then y = -3(1) + 5 = 2
The points are (-1, 8), (0, 5), (1, 2).
If x and y values of the point are zero then it passes through the origin.
The equation did not passes through the origin.

For Problems 10—11, write the slope-intercept form of the line with the given slope and point.

Question 10.
m = 4; (2, 3)
Answer:
Given that,
m = 4
Point = (2, 3)
The slope-intercept form of the line is y = mx + b
Therefore 3 = 4(2) + b
3 = 8 + b
b = 3 – 8
b = -5
The equation of the line is y = 4x – 5.

Question 11.
m = -2; (5, 1)
Answer:
Given that,
The slope = m = -2
Point = (5, 1)
The slope intercept form of the line is y = mx + b
Therefore 1 = -2(5) + b
1 = -10 + b
b = 1 + 10
b = 11
The equation of the line is y = -2x + 11.

Question 12.
Reason Which graph is steeper, y = -20x + 1 or y = 10x + 1?
Answer:
If we have a greater slop then it is steeper.
The slope of y = -20x + 1 = -20
The slope of y = 10x + 1 is 10.
The graph y = 10x + 1 have the greater steeper.

Question 13.
A. On the coordinate plane provided, plot the points (-2, -2), (-1, 1), and (1, 7). Connect the points with a straight line.

_______________
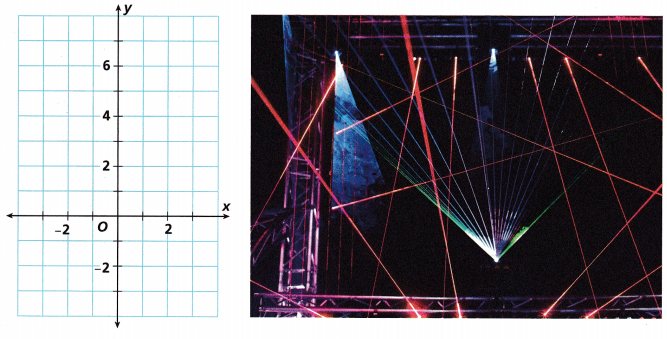
Answer:
Given that the coordinate points are (-2, -2), (-1, 1), (1, 7).

B. For each 1 unit increase in x, how much does y increase? What is the name for this value?
_______________
Answer:

C. Does the line pass through the origin? What is the y-intercept?
_______________
Answer: No, the line does not pass through the origin.
The Y-intercept is 4.

D. What is the equation of the line in slope-intercept form?
_______________
Answer:

E. Is the line with the equation y = 3x + 1 parallel to the line from Part A? Explain. (Hint: Graph the lines.)
_______________
Answer:

I’m in a Learning Mindset!

How is finding parallel lines to an equation in slope-intercept form a challenge?

Lesson 6.2 More Practice/Homework

Question 1.
Reason Tasha wants to graph a line that is parallel to the line with equation y = 3x. Give two examples of linear equations that represent lines she could draw: one that is above the original line and one that is below the original line.
Answer:
Given that,
The equation is y = 3x
If the two lines are parallel then the slope of two lines are equal.
The slope is 3
The equation above y = 3x is y = 3x + 2
The + 2 shifts the line up by 2 on the y axis.
The equation below y = 3x is y = 3x – 3
The -3 shifts the line down by 3 on the y axis.

Question 2.
Shyann is trying to figure out if the line with equation y = 5683x + 976 will pass through the origin. Will the line pass through the origin? How do you know?
Answer:
Given that the equation is
y = 5683x + 976
If x = -1 then y = 5683(-1) + 976 = -4707
If x = -2 then y = 5683(-2) + 976 = -10,390
If x = 0 then y = 5683(0) + 976 = 976
If x = 1 then y = 5683(1) + 976 = 6,659
If x = 2 then y = 5683(2) + 976 = 12,342
The coordinate points are (-1, -4707), (-2, -10,390), (0, 976), (1, 6,659), (2, 12,342).
If x and y values of the point are zero then it passes through the origin.
The equation of the line is not passes through the origin.

Question 3.
Paulo identifies one point on a line as (6, 3), and he knows that the slope is 2. How can he derive the equation of the line?
Answer:
Given that the points is (6, 3).
The slope = 2
The equation of the line is in the form of y = mx + b
3 = 2(6) + b
3 = 12 + b
b = 3 – 12
b = -9
Therefore the equation of the line is y = 2x – 9

Question 4.
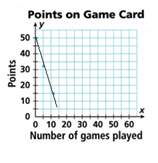
Math on the Spot An arcade deducts 3.5 points from a 50-point game card for each game played. The linear equation y = -3.5x + 50 represents the number of points y on a card after x games played. Graph the equation using the slope and y-intercept.

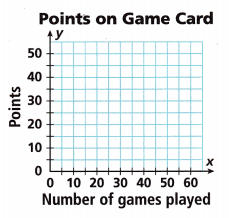
Answer:
Given that the linear equation is y = -3.5x + 50
If x = 0 then y = -3.5(0) + 50 = 50
If x = 5 then y = -3.5(5) + 50 = 32.5
If x = 10 then y = -3.5(10) + 50 = 15
The points are (0, 50), (5, 32.5), (10, 15).

For Problems 5-6. wrIte each equation In slope-Intercept form and identify the y-intecept

Question 5.
5 = 10x – 5y
Answer:
Given that the equation is 5 = 10x – 5y
The slope intercept form of the equation is y = mx + c
-5y = 5 – 10x
5y = 10x -5
y = 10x – 5/5
y = 2x – 1
Therefore the equation in slope-intercept form is y = 2x – 1.

Question 6.
12x = -4y – 8
Answer:
The slope intercept form of the equation is y = mx + c
The equation is 12x = – 4y – 8
12x + 8 = -4y
y = 12x + 8/-4
y = -3x -2
Therefore the equation in slope-intercept form is y = -3x – 2

For Problems 7-8, find the slope of the graph of the linear equation and indicate whether the graph rises or falls.

Question 7.
y = 3x – 11
Answer:
Given that,
The equation is y = 3x – 11
If x = 0 then y = 3(0) – 11 = -11
If x = 1 then y = 3(1) – 11 = 3 – 11 = -8
If x = 2 then y = 3(2) – 11 = 6 – 11 = -5
Therefore the equation is nonlinear and the graph falls down.

Question 8.
y = –\(\frac{1}{2}\)x + 2
Answer:
Given that the equation is
y = -1/2x + 2
If x = 1 then y = -½(1) + 2 = 1.5
If x = 2 then y = -½(2) + 2 = 1
If x = 3 then y = -½(3) + 2 = 0.5
Therefore the equation is nonlinear and the graph falls down.

For Problems 9-10, identify the function as linear or nonlinear.

Question 9.
y = \(\frac{3}{2}\)x + 9
Answer:
Given that the function is
y = 3/2x + 9
If x = 1 then y = 3/2(1) + 9 = 10.5
If x = 2 then y = 3/2(2) + 9 = 12
If x = 3 then y = 3/2(3) + 9 = 13.5
Therefore the function is linear. Because the x and y values are continuously increasing.

Question 10.
y = \(\frac{3}{2 x}\) + 9
Answer:
Given that,
y = 3/2x + 9
If x = 1 then y = 3/2(1) + 9 = 10.5
If x = 2 then y = 3/2(2) + 9 = 12
If x = 3 then y = 3/2(3) + 9 = 13.5
Therefore the function is linear. Because the x and y values are continuously increasing.

Test Prep

Question 11.
Find the equation of a line with slope -2 that contains the point (-3, 3).
y = x –
Answer:
Given that,
Slope = -2
Point = (-3, 3)
The equation of the line is y = mx + b
3 = -2(-3) + b
3 = 6 + b
b = 3 – 6
b = -3
Therefore the equation is y = -2x -3.

For Problems 12—14, complete each statement for the equation y = \(\frac{1}{2}\)x – \(\frac{1}{2}\)

Question 12.
Is the equation linear or nonlinear? _______________
Answer:
Given that the equation is
y = 1/2x – ½
If x = 0 then y = ½ (0) – ½ = – 0.5
If x = 1 then y = ½ (1) – 1/2 = 0
If x = 2 then y = ½ (2) – ½ = 0.5
If x = 3 then y = ½ (3) – ½ = 1
Therefore the given equation is linear. Because the x and y values are continuously increasing.

Question 13.
Is the equation a function? __________
Answer:
The equation is y = 1/2x – ½
If x = 0 then y = ½ (0) – ½ = – 0.5
If x = 1 then y = ½ (1) – 1/2 = 0
If x = 2 then y = ½ (2) – ½ = 0.5
If x = 3 then y = ½ (3) – ½ = 1.
The function of an equation means that has only one answer for y for every x.
Therefore the given equation is a function.

Question 14.
The graph crosses the y-axis at (o, ____).
Answer:
Given that the equation is
y = 1/2x – ½
If x = 0 then y = ½ (0) – ½ = – 0.5
The graph crosses the y axis at (0. -0.5).

Question 15.
Roscoe has a pie baking business. His profit is given by the linear equation y = 15x — 5. Sheena has a cake baking business. Her profit is given by an equation with a graph that is parallel to the graph of the equation for Roscoe’s profit. Which equation could be the equation for Sheena’s business?
A. y = 15x + 10
B. y = 3x – 1
C. y = 5x – 5
D. y = -15x – 3
Answer: A. y = 15x + 10
Explanation:
Given,
Roscoe has a pie baking business. His profit is given by the linear equation y = 15x — 5. Sheena has a cake baking business.
Her profit is given by an equation with a graph that is parallel to the graph of the equation for Roscoe’s profit.
y = mx + b
Because the two lines are parallel to each other.
So, they have the same slope.
Hence y = 15x + 10

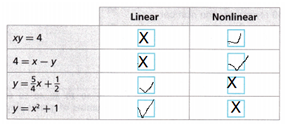
Question 16.
Identify whether each equation is linear or nonlinear.

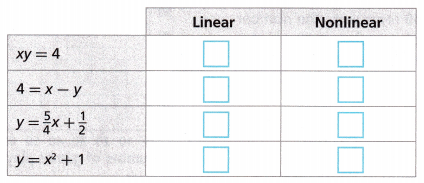
Answer:
Given that,
xy = 4
y = 4/x
If x = 1 then y = 4/1 = 4
If x = 2 then y = 4/2 = 2
It is a nonlinear equation.
4 = x – y
y = x – 4
If x = 1 then y = 1 – 4 = -3
If x = 2 then y = 2 – 4 = -2
It is a nonlinear equation.
y = 5/4 x + 1/2.
If x = 1 then y = 5/4(1) + 1/2 = 1.75
If x = 2 then y = 5/4(2) + 1/2 = 3
It is a linear equation.
y = x² + 1
If x = 1 then y = 1²  + 1 = 2
If x = 2 then y = 2²  + 1 = 5
It is a linear equation

Spiral Review

Question 17.
Mr. Chin asked his class to solve for y in the equation 8(3y – 5) = 9(y – 5) – 1. Explain how to solve for y. Then solve.
Answer:
8(3y – 5) = 9(y – 5) – 1
24y – 40 = 9y – 45 – 1
24y – 40 = 9y – 46
24y – 9y = 40 – 46
15y = -6
y = -6/15
y = -2/5

Question 18.
Luna knows a line crosses the y-axis at (0, -1). She also knows that the point (3, 2) is on the line. What is the slope of this line?
Answer:
Given,
Luna knows a line crosses the y-axis at (0, -1).
She also knows that the point (3, 2) is on the line.
m = (y2 – y1)/(x2-x1)
m = (2-(-1))/3
m = 3/3
m = 1

Question 19.
The slope of a line is 3. The point (1, 4) is on the line, Is the point (0, 1) on the line?
Answer:
slope = 3
passes point = (1, 4)
y – y1 = m(x – x1)
y – 4 = 3(x – 1)
y – 4 = 3x – 3
y = 1
1 – 4 = 3x – 3
-3 + 3 = 3x
x = 0
So yes the point (0, 1) on the line.