Into Math Grade 8 Module 5 Lesson 2 Answer Key Derive y = mx

We included HMH Into Math Grade 8 Answer Key PDF Module 5 Lesson 2 Derive y = mx to make students experts in learning maths.

HMH Into Math Grade 8 Module 5 Lesson 2 Answer Key Derive y = mx

I Can write the equation of a line given a graph or a table of values.

Spark Your Learning
Asiah’s literature class is studying a new book. To complete the assigned reading on time, she has made a schedule. Asiah records her progress in a graph. What can you interpret from the graph?

Turn and Talk How would the graph look differently if she read more pages per day?

Build Understanding

1. Use the graph of Asiah’s reading to answer the following questions.
A. The number of pages that Asiah has cumulatively read increases by

B. The graph shows the number of pages that Asiah has read at the end of each day. Complete the table, including a general expression for the number of pages Asiah will read in x days.

C. Use the variable y to stand for the number of pages that Asiah has read. Write an equation to model the number of pages read after x days.
____________________________
D. From the point at 1 day to the point at 2 days, how much does the graph rise?
____________________________
E. What is the slope, or rise over run, for Asiah’s graph? Explain your reasoning.
____________________________
F. How is the slope related to the unit rate of this proportional relationship?
____________________________
G. Look at the equation from Part C. What do you notice about the equation when you compare it to the slope from Part E?
____________________________
H. Asiah decides she wants to adjust her schedule so she will finish the book earlier than the due date. How will this change the slope? Explain your reasoning.
____________________________
____________________________

Step It Out

2. Don is a gifted wood carver, and he has started selling his wood carvings online. He tracks the total number of carvings sold.

A. The ratios of carvings sold to months in business (are / are not) equal for each row in the table. The relationship between the number of months in business and the number of carvings sold (is /is not) a
proportional relationship.
B. Sketch a graph of the relationship described by the table. Explain how the line supports your conclusion from Part A.

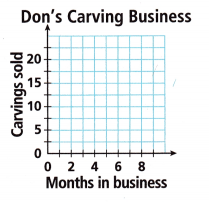
The graph of the relationship (is / is not) a straight line passing through the origin, so the relationship (is/is not) proportional.
C. Complete the rise over run to find the slope of the line.
The slope is
D. Complete the linear equation to model Don’s sales.

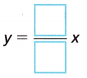
Connect to Vocabulary
A linear equation is an equation whose solutions form a straight line on a coordinate plane.

E. Use the graph to predict the number of carvings sold after being in business for 10 months.
_______________
F. Use the equation to predict the number of months needed for Don to sell 30 carvings online.
_______________

3. A digital thermometer records the temperature each hour. The graph shows how the temperature T has been changing each hour h.


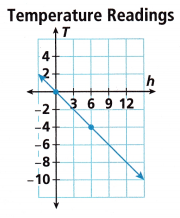
A. Describe how the temperature changes from midnight, h = 0, to 3 AM.
The temperature drops °C.
B. Between h = 0 and h = 3, describe the rise and run of the graph.
The rise is and the run is .
C. Use the rise over run to write the slope of the graph.
The slope is ____.
D. Write an equation of the line in the form T = mh.
_______________________
Answer:
T = kh
when h = 6 and T = -4
-4 = 6k
k = -2/3
T = -2/3h
T = -2/3 × 3 = -2
Thus the temperature drops 2°C

Turn and Talk A line is modeled by the equation y = mx. Explain how the value of m affects the graph of the line.
Answer:
We have the slope-intercept form of a straight line given by y = mx + b, where m is the slope and b is the y-intercept.
If b = 0
then y = mx

Check Understanding

Question 1.
The Nguyen family is traveling cross-country, driving 300 miles each day. Let x represent the number of days in the trip and let y represent the total number of miles driven. Write an equation to model their trip.
Answer:
Given,
The Nguyen family is traveling cross-country, driving 300 miles each day.
Let x represent the number of days in the trip and let y represent the total number of miles driven.
y = 300x
Thus the equation to model their trip is y = 300x

Question 2.
Write the equation for the line passing through points (0, 0), (4, 5), and (8, 10).
Answer:
From the coordinate, (0, 0), we can conclude that the y-intercept of the line is 0.
(4, 5) and (8, 10)
Slope = (y2-y1)/(x2-x1)
m = (10 – 5)/(8 – 4)
m = 5/4
Thus the equation of the line is y = 5/4x

On Your Own

Question 3.
Reason A clothing store is going out of business. To sell their remaining inventory, the managers drop the price of each item $5 at the end of each week until the item sells.

A. After 5 weeks, how will the price of an item have changed?
________________________
Answer:
1 week = $5
5 weeks = x
x = 5 × $5 = $25
After 5 weeks the price of an item will be changed to $25.

B. A line is drawn to model the relationship between the number of weeks and the change in price. Is the slope of this line positive or negative? Explain.
________________________
Answer:

C. Write the equation of the line.
________________________
Answer:

Question 4.
A line passes through the origin, (5, -15), and (-1, 3).
A. Explain how to find the slope of the line.
Answer:
Let the analytical formula of the straight line be y = kx + b
(5, -15), and (-1, 3)
Slope = (y2-y1)/(x2-x1)
m = (3+15)/(-1-5)
m = 18/-6
m = -3

For Problems 5-8. write the equation of the line shown.

Question 5.

_______________
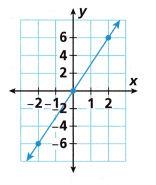
Answer:
We have two points (x1, y1) and (x2, y2)
(6, 2) and (-2, -3)
Slope = (y2-y1)/(x2-x1)
m = (-3-2)/(-2-6)
m = 5/8

Question 6.

_______________
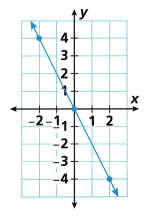
Answer:
We have two points (x1, y1) and (x2, y2)
(-2, 4) and (2, -4)
Slope = (y2-y1)/(x2-x1)
m = (-4-4)/(2+2)
m = -8/4
m = -2

Question 7.

_______________
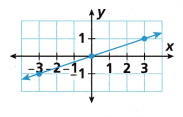
Answer:
We have two points (x1, y1) and (x2, y2)
(3, 1) and (-3, -1)
Slope = (y2-y1)/(x2-x1)
m = (-1-1)/(-3-3)
m = -2/-6
m = 1/3

Question 8.

_______________
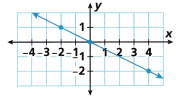
Answer:
We have two points (x1, y1) and (x2, y2)
(-2, 1) and (4, -2)
Slope = (y2-y1)/(x2-x1)
m = (-2-1)/(4+2)
m = -3/6
m = -1/2

For Problems 9-10, sketch the graph of the line represented by the equation. Plot and label three points on each line.

Question 9.
y = \(\frac{5}{3}\)x

Answer:

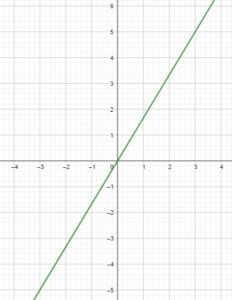
Question 10.
y = –\(\frac{1}{4}\)x

Answer:
x = 0
y = 1/4(0)
y = 0
x = 1
y = 1/4(1)
y = 1/4
x = 2
y = 1/4(2)
y = 1/2

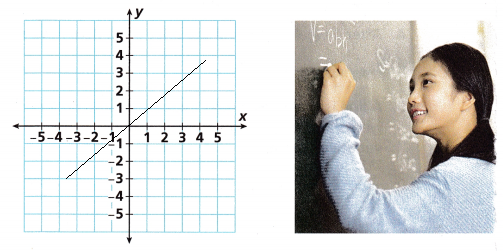
For Problems 11-12, write an equation that models the relationship shown in the table.

Question 11.

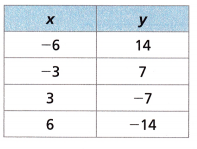
Answer:
Let the analytical formula of the straight line be y = kx + b
(-6, 14) and (-3, 7)
14 = -6k + b
b = 0
14 = -6k
k = -7/3
y = -7/3x

Question 12.

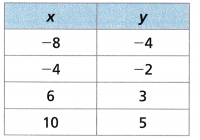
Answer:
Let the analytical formula of the straight line be y = kx + b
(-8, -4) and (-4, -2)
-8k + b = -4
b = 0
-8k = -4
k = 1/2
y = 1/2 x

For Problems 13-14, write an equation for the line described.

Question 13.
a line passing through the origin and (-2.5, 5)
_______________________
Answer:
The line passing through the origin.
y = kx
x = -2.5 and y = 5
5 = k . -2.5
k = -5/2.5
k = -2
So, slope is -2

Question 14.
a line passing through the origin and (3a, 5g)
Answer:
The line passing through the origin.
y = kx
x = 3a and y = 5g
5g = k . 3a
k = 3a/5g . x
So, the equation is y = 5g/3a . x

I’m in a Learning Mindset!

What challenge did I face when writing an equation that modeled the relationship in the table for Problem 12?
______________________________
______________________________

Lesson 5.2 More Practice/Homework

Question 1.
Sean tutors math students to earn extra money.

A. How much would Sean earn from 4 hours of tutoring?
______________________________
______________________________
Answer:
Sean earn $20 per hour
4 hours = 4 × 20 = $80

B. Write an equation to model Sean’s earnings, y, after x hours.
______________________________
Answer:
y = 20x
where x represents number of hours and y represents earnings.

Question 2.
Attend to Precision An inch is exactly 2.54 centimeters. Write an equation to convert the number of inches x to the corresponding length in centimeters.
Answer:
Given,
An inch is exactly 2.54 centimeters.
1 cm = 0.39 inch
y = 2.54x

Question 3.
Write an equation of the line passing through the points (-5, -25), (0, 0), and (3, 15).
Answer:
(-5, -25), (0, 0), and (3, 15)
-25 = m(-5) + b ⇒ 5m – b = 25
0 = m(0) + b ⇒ b = 0
5m – 0 = 25
5m = 25
m = 5
5m – b = 25
5(5) – b = 25
25 – b = 25
25 – 25 = b
b = 0
y = mx + b
y = 5x + 0
y = 5x

Question 4.
Math on the Spot The graph shows the distance Caleb runs over time.
A. Identify four points on the line.
_______________________
Answer: Four points on the line are (0, 0), (8, 1), (16, 2) and (24, 3)

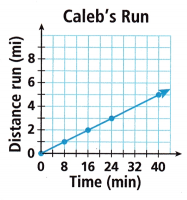
B. Determine the slope of the line.
_______________________
Answer:
8 min = 1 mile
1 min = 1/8 mile
y = kx
k = 1/8
So, the slope of the line is 1/8.

C. Write an equation of the line.
_______________________
Answer:
If y = kx + b
k = 1/8 and b = 0
Thus the equation of the line is y = 1/8 x

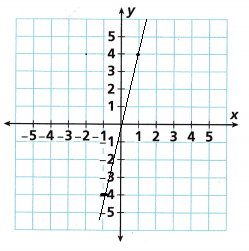
Question 5.
Sketch the graph of the line y = 4x.

Answer:
y = 4x
x = 0
y = 4(0) = 4
x = 1
y = 4(1) = 4
x = 2
y = 4(2) = 8
x = -1
y = 4(-1) = -4
x = -2
y = 4(-2) = -8

Question 6.
Write an equation that models the relationship shown in the table.

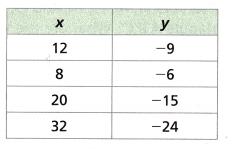
Answer:
-9/12 = -3/4
So, the equation would be,
y = -4/3 x
y = -3/4(12) = -9
y = -3/4(8) = -6
y = -3/4(20) = -15
y = -3/4(32) = -24

Test Prep

Question 7.
What is the equation of the line passing through the points (-2, 5), (0, 0), and (4, -10)?
A. y = –\(\frac{5}{2}\)x
B. y = –\(\frac{2}{5}\)x
C. y = \(\frac{2}{5}\)x
D. y = \(\frac{5}{2}\)x
Answer:
Given points (-2, 5), (0, 0), and (4, -10)
-2m + b = 5
m(0) + b = 0
b = 0
5 = -2m
m = -5/2
y = -5/2x
Thus option A is the correct answer.

Question 8.
Write the equation of the line passing through the points (0, 0), (2, 1), and (-2, -1).
y = x
Answer:
y = ax² + bx + c
4a + 2b = 1
4a – 2b = -1
8a = 0
a = 0
4a + 2b = 1
0 + 2b = 1
b = 1/2
So, y = 1/2x

Question 9.
The value of a house has been increasing by $5000 each year. Write an equation to show how the value will have changed x years from now.
y = x
Answer:
Given,
The value of a house has been increasing by $5000 each year.
y = 5000x

Question 10.
Graph y = \(\frac{2}{3}\)x.

Answer:

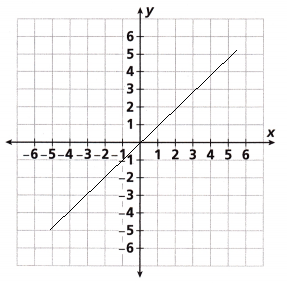
Spiral Review

Question 11.
Triangle ABC has vertices (1, 4), (5, 6), and (3, 10). It is reflected across the y-axis, forming Triangle A’B’C’. What are the vertices of the new triangle?
Answer:
Given,
Triangle ABC has vertices (1, 4), (5, 6), and (3, 10). It is reflected across the y-axis, forming Triangle A’B’C’.
A'(-1, 4), B'(-5, 6) and C'(-3, 10)

Question 12.
Quadrilateral ABCD is dilated by a scale factor of 2, with the center of dilation at the origin. The vertices of ABCD are A(0, 0), 8(5, 0), C(5, 3), and 0(0, 3). What are the coordinates of the image of Vertex C under the dilation?
Answer:

Question 13.
Solve the equation 3x – 2(x + 1) = 2x – 7.
Answer:
3x – 2(x + 1) = 2x – 7
3x – 2x – 2 = 2x – 7
x – 2x = 2 – 7
-x = -5
x = 5