Into Math Grade 8 Module 5 Lesson 1 Answer Key Explain Slope with Similar Triangles

We included HMH Into Math Grade 8 Answer Key PDF Module 5 Lesson 1 Explain Slope with Similar Triangles to make students experts in learning maths.

HMH Into Math Grade 8 Module 5 Lesson 1 Answer Key Explain Slope with Similar Triangles

I Can determine the slope of a line and use it to find additional points on the line.

Spark Your Learning
A line passes through the origin. Two right triangles each have one side along the line and another side on the x-axis. How is ∆OAC related to ∆OBD?

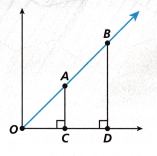
Turn and Talk Amie drew a different line through the origin and drew two new right triangles that have one side along the x-axis. How are her triangles different from the ones shown above? How are they the same?

Build Understanding

1. Points on the line represent the vertical and horizontal distances a person would travel while climbing the path before steps were built to make the climb easier.

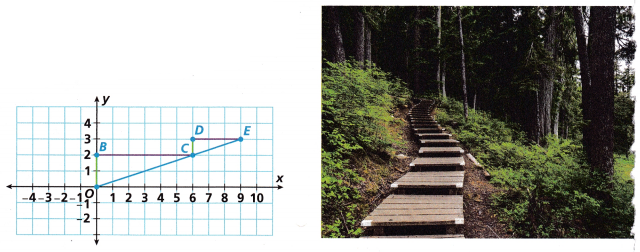
A. Write a sequence of transformations that maps one triangle onto the other to show that ∆OBC is similar to ∆CDE.

Connect to vocabulary
The hypotenuse of a right triangle is the side opposite the right angle. The legs of a right triangle are the sides adjacent to the right angle.

B. Complete the following based on ∆OBC and ∆CDE.

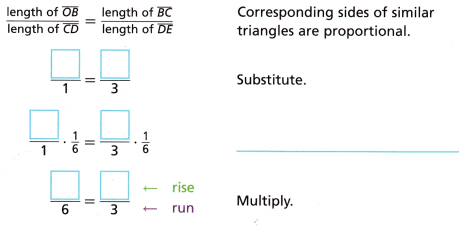
C. When moving from one point to another along a line, the change in the y-coordinates is the nse and the change in the x-coordinates is the run. The legs of ∆OBC and ∆CDE can help you visualize the rise and run. What does Part B show you about the rise-to-run ratios in ∆OBC and ∆CDE?

Step It Out

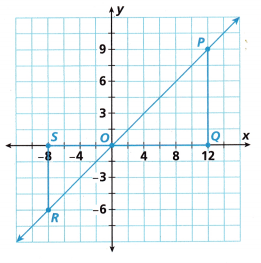
2. A skateboard ramp is shown on a coordinate plane.


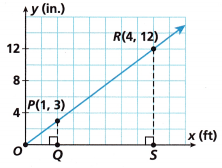
A. Line OP passes through the origin, Point P, and Point R.
The coordinates of Point Q are , and the coordinates of Point S are .
B. Does this line represent a proportional relationship? Explain.
________________________
C. Since the run between the origin and Point P is 1, the unit rate is equal to the rise-over-run ratio. Find the unit rate of the relationship modeled by the line. Complete the equation using the coordinates of Point P and the origin.

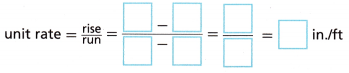
Connect to Vocabulary
A rate is a comparison of two quantities that have different units. A unit rate is a rate with a denominator of one unit.

D. A vertical line segment from Point R to the x-axis forms a right triangle, ∆ORS. Complete the statements to show ∆OPQ is similar to ∆ORS.
m∠POQ is equal to m∠. ∠OQP and ∠ are right angles, so they are also (congruent / similar). By the AA Similarity Postulate, ∆QPQ is similar to ∆.
E. Find the rise-over-run relationship modeled by the line, using the coordinates of Point R and the origin.

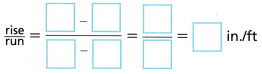
Connect to Vocabulary
Slope is a measure of the steepness of a line and is described by the ratio of the line’s rise to its run. A horizontal line has slope 0, and a vertical lines slope is undefined.

F. Describe the slope of the line. The rise-over-run ratio, or slope, between the origin and Point P is (equal to / not equal to) the rise-over-run ratio, or slope, between the origin and Point R. The slope of the line is (constant /not constant).

3. Points M(2, 3) and N(x, -6) lie on the same line. The line also passes through the origin.

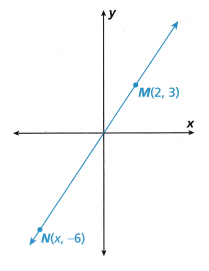
A. For a line passing through the origin, what do you notice about measuring rise over run from the origin to another point on the line?
________________________
________________________

B. Find the rise over run from the origin to Point M.

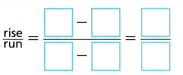
Answer:

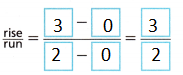
C. The rise-over-run ratio, or slope, of any line is constant. Use this ratio to write an equation that can help you find the x-coordinate of Point N.


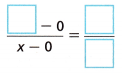
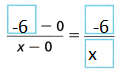
D. Use proportional reasoning to solve for x.
x = ___
-6 = 3/2 (x)
-6 × 2 = 3x
-12/3 = x
x = -4

Turn and Talk Explain, using the rise and the run, wny the slope or a horizontal line is 0.

Check Understanding

Question 1.
Explain how dilation scale factors can help you identify points on a line passing through the origin given one additional point.
Answer:

Question 2.
A line passes through the origin and (5, 3). Identify two additional points on this line.
Answer:
A line passes through the origin and (5, 3).
The two additional points are (-5, -3) and (-5, 3).

On Your Own

Question 3.
A road sign is posted showing a road has a 10% grade, meaning the ratio of vertical to horizontal distance is 10%, or \(\frac{1}{10}\). If a car driving on the road rises from an elevation of
543 feet above sea level to an elevation of 768 feet above sea level, how far has the car traveled horizontally?

Answer:
Given,
A road sign is posted showing a road has a 10% grade, meaning the ratio of vertical to horizontal distance is 10%, or \(\frac{1}{10}\).
If a car driving on the road rises from an elevation of 543 feet above sea level to an elevation of 768 feet above sea level.
h = 768-543 = 225 ft
tanθ = 1/10 = h/x = 225/x
x = 225 × 10 = 2250
y = √(x² + h²)
y = √2250² + 225²
y = 2261.22 ft

Question 4.
Attend to Precision Line l passes through the origin and the point (4, 5). Suppose point (x, y) also lies on Line l.
A. The slope of Line e from the origin to (4, 5) is ________________________
Answer:

B. Why is the slope of Line l from the origin to (x, y) the same as the slope from the origin to (4, 5)?
Answer:

Question 5.
Are Triangles OPQ and ORS similar? If so, give a sequence of transformations that maps △OPQ onto △ORS.

Answer:

For Problems 6—9. find the value of k given that both points lie on a line passing through the origin.

Question 6.
(5, 10) and (-3, k)
Answer:
Given that both points lie on a line passing through the origin.
(0, 0) and (5, 10)
m = (y2-y1)/(x2-x1)
m = (10-0)/(5-0) = 10/5 = 2
Substitute (-3, k) in y = mx
k = 2(-3)
k = -6

Question 7.
(-12, -2) and (k, 8)
Answer:
Given that both points lie on a line passing through the origin.
(0, 0) and (-12, -2)
m = (y2-y1)/(x2-x1)
m = (-2-0)/(-12-0) = -2/-12 = 1/6
Substitute (k, 8) in y = mx
8 = 1/6(k)
8 × 6 = k
k = 48

Question 8.
(k, 7) and (-81, -9)
Answer:
Given that both points lie on a line passing through the origin.
(0, 0) and (-81, -9)
m = (y2-y1)/(x2-x1)
m = -81/-9 = 9
m = 9
Substitute (k, 7) in y = mx
7 = 9k
k = 7/9

Question 9.
(k, -24) and (5, 40)
Answer:
Given that both points lie on a line passing through the origin.
(0, 0) and (5, 40)
m = (y2-y1)/(x2-x1)
m = (40-0)/(5-0)
m = 40/5 = 8
Substitute (k, -24) in y = mx
-24 = 8k
k = -3

Question 10.
At the bottom of a mountain, a ski lift starts four feet above the ground. At the top of the mountain, the lift is 1356 feet higher. If the lift ascends one foot for every four feet it travels west, how far west of the starting position is the lift at the top of the mountain?

Answer:
Given,
At the bottom of a mountain, a ski lift starts four feet above the ground. At the top of the mountain, the lift is 1356 feet higher.
1356 – 4 = 1352 feet
1352 × 4 = 5408 feet
So, the ski lift travels 5408 feet west.

For Problems 11—13. use the given information.

STEM Kylie is preparing for the science fair which will take place in six weeks. She has three plants that she has grown from seeds, which she considers to have height o centimeters, and she is measuring their heights as she applies different treatments to each.

Question 11.
The first plant is receiving Plant Food A. After 4 weeks, it is 10 centimeters tall, as shown. If it continues growing at this rate, how tall will it be after 6 weeks?
Answer:
Given,
The first plant is receiving Plant Food A. After 4 weeks, it is 10 centimeters tall, as shown.
6 × (10 ÷ 4)
6 × 2.5 = 15 centimeters
Thus the plant will be 15 centimeters tall after 6 weeks.

Question 12.
The second plant is receiving Plant Food B. After 3 weeks, it is 10 centimeters tall. If it continues growing at this rate, how tall will it be after 6 weeks?
Answer:
Given,
The second plant is receiving Plant Food B. After 3 weeks, it is 10 centimeters tall.
10 ÷ 3 = 3.3
3.3 × 6 = 19.8 ≈ 20 centimeters

Question 13.
The third plant is planted in the same soil as the others, but it receives only light and water. After 2 weeks, it is 6 centimeters tall. If it continues growing at this rate, how tall will it be after 6 weeks?
Answer:
Given,
The third plant is planted in the same soil as the others, but it receives only light and water.
After 2 weeks, it is 6 centimeters tall.
So, the ratio is 2 week:6 centimeter
2/2 = 1 and 6/2 = 3
So, the ratio is 1:3
We multiply those by the number of weeks: 6
1 × 6 = 6 and 3 × 6 = 18
The ratio is 6:18
Thus the plant will be 18 centimeters after 6 weeks.

Use Repeated Reasoning In Problems 14—16, a point is given that lies on a line passing through the origin. Identify four additional points that lie on the line. Include two points with positive coordinates and two points with negative coordinates.

Question 14.
(17, 51) ________________________
Answer:
The four additional points are (17, 51), (-17, -51), (-17, 51) and (17, -51)

Question 15.
(72, 18) ________________________
Answer: The four additional points are (72, 18), (-72, -18), (-72, 18) and (72, -18)

Question 16.
(-8, -5) ________________________
Answer: The four additional points are (-8, -5), (8, 5), (-8, 5) and (8, -5)

Question 17.
A line passes through (6, 3), (8, 4), and (n, -2). Find the value of n.
Answer:
A line passes through (6, 3), (8, 4), and (n, -2).
m = (y2-y1)/(x2-x1)
m = (4-3)/(8-6) = 1/2
y = 1/2x + b
We need to find the value of b.
Let’s use (8,4) point and plug it into our linear equation: y = 1/2x+b
4 = 1/2(8) + b
4 – 4 = b
b = 0
The problem gives us (n, -2)
-2 = 1/2(n)
-2 × 2 = n
n = -4

Question 18.
A line passes through (-2, 4), (-4, 8), and (n, -4). Find the value of n.
Answer:
A line passes through (-2, 4), (-4, 8), and (n, -4).
m = (y2-y1)/(x2-x1)
m = (8-4)/(-4+2) = 4/-2 = -2
y = -2x + b
We need to find the value of b.
Let’s use (-4,8) point and plug it into our linear equation: y = -2x+b
8 = (-2)(-4) + b
b = 8 – 8 = 0
b = 0
y = -2x
The problem gives us (n, -4) where -4 y, so we plug in -4 as y in the equation to get:
-4 = -2n
n = 2

I’m in a Learning Mindset!

How was finding additional points that lie on a line an appropriate challenge for me?

Lesson 5.1 More Practice/Homework

Use the graph to answer Problems 1-4.

Question 1.
How is ∆PQR related to ∆STU?

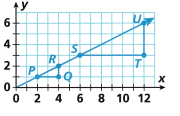
Answer:
∆PQR is similar to ∆STU.
As shape of both the triangles is the same.

Question 2.
Describe a sequence of transformations that maps ∆PQR onto ∆STU.
Answer:

Question 3.
Identify one pair of corresponding angles and describe what you know about them.
Answer:

Question 4.
What is the ratio of the length of the vertical side to the length of the horizontal side of each triangle? What is the slope of the line?
Answer:

Question 5.
Model with Mathematics A person casts a shadow that aligns with the shadow of a tree. The person is 5.5 feet tall, and casts a shadow 8.25 feet long. The treets shadow measures 22.5 feet long.
A. Write an equation you can use to find the tree’s height.
________________________
Answer:

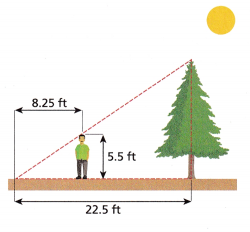
B. How tall is the tree? How far is the person 22.5 ft standing from the tree?
________________________
Answer:

Question 6.
Open Ended Explain how it is possible to find the slope of a line given any two points on the line.
Answer:
Yes, by using the formula for finding the slope of the line in two points form.
Suppose any two points on the line be (x1, y1) and (x2, y2)
Slope of the line = (y2-y1)/(x2-x1)

Test Prep

Question 7.
A line passes through the origin, (3, 5), and (-12, b). What is the value of b?
A. -20
B. -1o
C. -7
D. 20
Answer:
m = (5- 0)/(3 – 0)
m = 5/3
y = mx
b = (5/3) (-12)
b = 5 × -4
b = -20
Thus option A is the correct answer.

Question 8.
A line passes through the origin and (8, 2). Select all points that lie on this line.
A. (-8, -2)
B. (-4, -1)
C. (-2, -8)
D. (-1, 1)
E. (16, 4)
F. (40, 10)
Answer:
m = (0-2)/(0-8) = -2, -8
x = -2 and y = -8
So, (-2, -8) is the answer.

Question 9.
A line passes through the origin, (-1, 1), and (4, n). Find the value of n.
n = __
Answer:
m = (1-0)/(-1-0) = -1
y = mx
n = (-1)(4)
n = -4

Spiral Review

Question 10.
Find the value of x. Then find the measure of each angle.
________________________

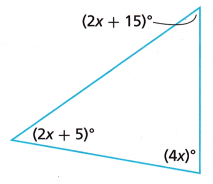
Answer:
We know that,
Sum of angles = 180°
(2x + 15) + (2x + 5)° + 4x° = 180°
2x + 2x + 4x + 20 = 180°
8x + 20 = 180°
8x = 180° – 20°
8x = 160°
x = 160/8
x = 20°
Now substitute the value of x in the given angle measures.
2x + 15
2(20) + 15 = 40 + 15 = 55°
2x + 5
2(20) + 5 = 45°
4x = 4(20) = 80°

Question 11.
Ben can buy 5 notebooks for $6.75 at Store A or 3 notebooks for $4.50 at Store B. Which store offers the better value?
Answer:
Given,
Ben can buy 5 notebooks for $6.75 at Store A
Cost of  notebook = 6.75/5 = $1.35
So, the cost of 1 book in store A is $1.35
3 notebooks for $4.50 at Store B
Cost of 1 notebook = $4.50/3 = $1.50
Store A offers a better price than Store B.

Question 12.
Describe a transformation that maps ABCD onto A’B’C’D’.

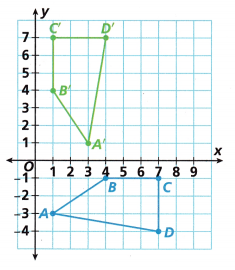
Answer:
A transformation is a general term for four specific ways to manipulate the shape and/or position of a point, line, or geometric figure.
The above graph is a reflection in 90 degrees anticlockwise direction.)