We included HMH Into Math Grade 8 Answer Key PDF Module 4 Lesson 1 Develop Angle Relationships for Triangles to make students experts in learning maths.
HMH Into Math Grade 8 Module 4 Lesson 1 Answer Key Develop Angle Relationships for Triangles
I Can find an unknown angle measure in a triangle.
Spark Your Learning
The angles of a triangle have a relationship with each other. Draw three unique triangles. What do you notice about the measures of the interior angles of the triangles?


Turn and Talk What conjecture can you make about the sum of the measures of the angles of a triangle?
Build Understanding
1. What is the sum of the measures of the three interior angles of a triangle?
A. Find the sum of the measures of the angles in each of the three triangles.
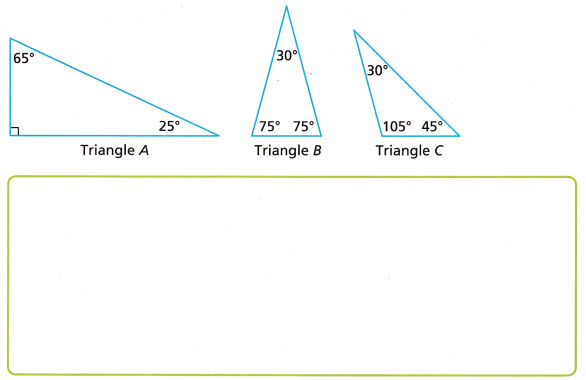
Answer:
Triangle A:
90° + 25° + 65°
90° + 90° = 180°
Triangle B:
75° + 75° + 30° = 150° + 30° = 180°
Triangle C:
105° + 45° + 30° = 150° + 30° = 180°
B. What do you notice about the sum of the measures of the three triangles?
____________________
Answer:
The sum of the measures of the three triangles is 180°
C. Do you think this is true for all triangles? Explain.
____________________
The Triangle Sum Theorem states that the measures of the three interior angles of a triangle sum to 180°.
D. The angles in a triangle measure 2x, 3x, and 4x degrees. Write and solve an equation to determine the angle measures.
____________________
____________________
Answer:
The angles in a triangle measure 2x, 3x, and 4x degrees.
The sum of the measures of the three triangles is 180°
2x + 3x + 4x = 180°
9x = 180°
x = 180/9
x = 20°
2x = 2 × 20 = 40°
3x = 3 × 20 = 60°
4x = 4 × 20 = 80°
Turn and Talk Discuss how to find a missing measure of an angle in a triangle when the other two angle measures are given.
Step It Out
The Triangle Sum Theorem can be used to draw conclusions about a triangle’s interior angles.
2. The dashed line segment represents an extension of one side of the triangle. Together with the right side of the triangle, the segment forms an angle, ∠4.

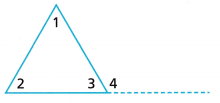
A. What is the sum of the measures of ∠3 and ∠4?
__________________
Answer:
the sum of the measures of ∠3 and ∠4 is 180°
B. An exterior angle of a polygon is an angle formed by one side of the polygon and the extension of an adjacent side. Which angle in the diagram is an exterior angle?
_____________
Answer: ∠4 is an exterior angle.
C. If the measure of ∠3 is 60°, what is the measure of ∠4?
_______________________
Answer:
∠3 = 60°
∠3 + ∠4 = 180°
60°+ ∠4 = 180°
∠4 = 180° – 60°
∠4 = 120°
D. If the measure of ∠3 is 60°, what is the sum of the measures of ∠1 and ∠2?
______________
Answer:
∠3 = 60°
∠1 + ∠2 + ∠3 = 180°
∠1 + ∠2 + 60° = 180°
∠1 + ∠2 = 180° – 60° = 120°
Thus the sum of the measures of ∠1 and ∠2 is 120°
E. Which angle has a measure equal to the sum of the measures of ∠1 and ∠2?
______________________________
Answer:
∠4 = 120°
∠1 + ∠2 = 180° – 60° = 120°
So, ∠4 has a measure equal to the sum of the measures of ∠1 and ∠2.
F. A remote interior angle of an exterior angle of a polygon is an angle that is inside the polygon and is not adjacent to the exterior angle. Which two angles in the diagram are remote interior angles in relation to Angle 4?
_____________________________
Answer: ∠1 and ∠2 are the remote interior angles in relation to Angle 4.
G. If the sum of the measures of ∠1 and ∠2 is 115°, what is the measure of ∠4?
_______________________
Answer:
If the sum of the measures of ∠1 and ∠2 is 115° then the measure of ∠4 is 115°.
Turn and Talk A triangle has exterior Angle P with remote interior Angles Q and R. Can you determine which angle has the greatest measure? Why or why not?
3. A machinist is drawing a triangular piece of an industrial machine.
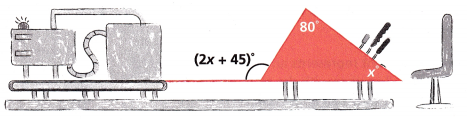
A. Write an equation and solve to find the value of x. Show your work.
___x + ___ = x + ___
__x – x = 80 – ___
x = ___
Answer:
2x + 45° = x + 80°
2x – x = 80° – 45°
x = 35°
B. What is the measure of the unknown remote interior angle?
_____________________
Answer: the measure of the unknown remote interior angle is 35°
C. Use the value of x from Part A to find the measure of the exterior angle.
2x + 45 = 2(___) + 45 = ___ + 45 = ___
Answer:
2x + 45
2(35) + 45
70° + 45° = 115°
Connect to Vocabulary
The measure of an exterior angle of a triangle is greater than either of the measures of the remote interior angles. This is the Exterior Angle Theorem.
D. What is the measure of the exterior angle?
__________________
Answer: the measure of the exterior angle is 115°
Check Understanding
Question 1.
Two angles of a triangle have measures of 30° and 45°. What is the measure of the remaining angle?
Answer:
Given,
Two angles of a triangle have measures of 30° and 45°.
Sum of three angles of a triangle = 180°
30°+ 45° + x° = 180°
75° + x° = 180
x° = 180° – 75°
x° = 105°
Question 2.
Dana draws a triangle with one angle that has a measure of 40°.
A. What is the measure of the angle’s adjacent exterior angle?
______________
Answer:
Dana draws a triangle with one angle that has a measure of 40°.
180°- 40° = 140°
Thus the measure of the angle’s adjacent exterior angle is 140°
B. What is the sum of the measures of the remote interior angles for the exterior angle adjacent to the 40° angle?
______________
Answer:
140° + 40° = 180°
Question 3.
An exterior angle of a triangle has a measure of 80°, and one of the remote interior angles has a measure of 20°. Write and solve an equation to find the measure of the other remote interior angle.
Answer:
Given,
An exterior angle of a triangle has a measure of 80°,
180° – 80° = 100°
and one of the remote interior angles has a measure of 20°.
180° – 20° – 100° = 60°
On Your Own
Question 4.
A puppeteer is making a triangular hat for a puppet. If two of the three angles of the hat both measure 30°, what is the measure of the third angle?
Answer:
x + 30° + 30° = 180
x + 60° = 180°
x = 180° – 60°
x = 120°
The triangle is an isosceles triangle and the measure of the third angle is 120°
Question 5.
Construct Arguments Can a triangle have two obtuse angles? Explain your answer.
Answer:
No, a triangle does not have two obtuse angles
Sum of three angles of a triangle = 180°
100 + 100 = 200° (Not possible)
Question 6.
STEM In engineering, equilateral triangles can support the most weight and so are commonly found in the design of bridges and buildings. Equilateral triangles are triangles with three congruent sides and three congruent angles. What are the measures of the angles of an equilateral triangle?
Answer:
x + x + x = 180°
3x° = 180°
x = 180/3
x = 60°
Question 7.
A triangle has one 30° angle, an unknown angle, and an angle with a measure that is twice the measure of the unknown angle. Find the measures of the triangle’s unknown angles and explain how you found the answer.
Answer:
Given,
A triangle has one 30° angle, an unknown angle, and an angle with a measure that is twice the measure of the unknown angle.
x + 2x + 30° = 180°
3x + 30° = 180°
3x = 180° – 30°
3x = 150°
x = 150/3
x = 50°
2x = 2 × 50 = 100°
For Problems 8-10, find the measures of the unknown third angles.
Question 8.

_____________
Answer:
Sum of three angles of a triangle is 180°
31.5° + 90° + x° = 180°
121.5° + x° = 180°
x° = 180° – 121.5°
x° = 58.5°
Thus the unknown angle is 58.5°
Question 9.
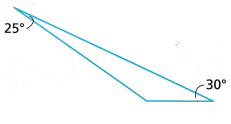
_____________
Answer:
Sum of three angles of a triangle is 180°
25° + x° + 30° = 180°
55° + x° = 180°
x° = 180° – 55°
x° = 125°
Thus the unknown angle is 125°
Question 10.
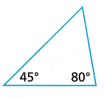
Answer:
Sum of three angles of a triangle is 180°
45° + 80° + x° = 180°
125° + x° = 180°
x° = 180° – 125°
x° = 155°
Thus the unknown angle is 155°
Question 11.
Open Ended The measure of an exterior angle of a triangle is x°. The measure of the adjacent interior angle is at least twice x. List three possible solutions for x.
Answer:
The measure of an exterior angle of a triangle is x°.
The measure of the adjacent interior angle is at least twice x.
x° + θ = 180°
θ = 180° – x ≥ 2x°
180° ≥ 3x°
0° < x ≤ 60°
Any three numbers in (0, 60).
Question 12.
The measure of an exterior angle of a triangle is 40°. What is the sum of the measures of the corresponding remote interior angles?
Answer:
The measure of an exterior angle of a triangle is 40°.
2x + 40° = 180°
2x = 180 – 40
2x = 140
x = 140/2
x = 70°
Thus the sum of the measures of the corresponding remote interior angles is 140°
Question 13.
Steven is building a fin for his surfboard. In order to make the fin, he needs to know the value of x in the following diagram. Use your knowledge of triangle angle relationships to find the value of x.

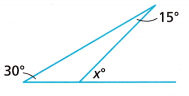
Answer:
Sum of three angles of a triangle is 180°
30° + 15° + y° = 180°
45° + y° = 180°
y° = 180° – 45°
y = 135°
135° + x = 180°
x° = 180° – 135°
x° = 45°
Question 14.
Find the value of x in the diagram. Explain how you found the answer.
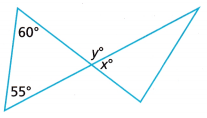
Answer:
x = y
y + 60° + 55° = 180°
y + 115° = 180°
y = 180° – 115°
y = 65°
So, x = 65°
I’m in a Learning Mindset!
What did I learn from applying my knowledge of interior angles of a triangle to find the missing exterior angle in Problem 13 that I can explain clearly to a classmate?
Lesson 4.1 More Practice/Homework
Question 1.
Find the value of x using your knowledge of the relationship between interior and exterior angles.
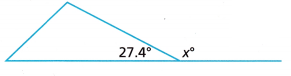
Answer:
Sum of interior and exterior angles is 180°
27.4° + x° = 180°
x° = 180° – 27.4°
x = 152.6°
Question 2.
Math on the Spot Find the unknown measure in the triangle.
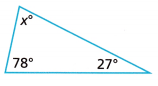
Answer:
x° + 78° + 27° = 180°
x° + 105° = 180°
x° = 180° – 105°
x° = 75°
Question 3.
Construct Arguments Can the measure of an exterior angle of a triangle ever exceed 180? Explain your reasoning.
Answer: An exterior angle of a triangle cannot be a straight line because a triangle has 180° in adding all the three angles of a triangle.
Question 4.
STEM The measure of the angle formed at the center of an oxygen atom in a water molecule is about 105°. The angles formed at each hydrogen atom are congruent. What is the size of the angle at each hydrogen atom?
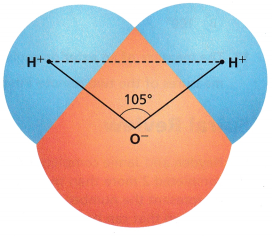
Answer:
Congruent angles are the ones that are the same in value, in the attached image we can see the atom, the O atom forms 105 with both H atoms, if we use trigonometry we have
x + x + 105° = 180°
2x + 105° = 180°
2x = 180 – 105
2x = 75
x = 75/2
x = 37.5°
Question 5.
Open Ended One of the angles in a triangle measures 90°. Name three possibilities for the measures of the remaining two angles.
Answer:
One of the angles in a triangle measures 90°
30° + 60° + 90° = 180°
90° + 45° + 45° = 180°
90° + 50° + 40° = 180°
Question 6.
Find the value of x in the following diagram.
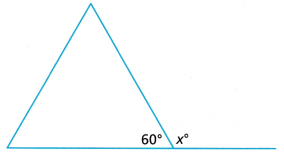
Answer:
x° + 60° = 180°
x° = 180° – 60°
x° = 120°
Thus the measure of angle x is 120.
Test Prep
Question 7.
Complete the táble by entering the measures of the unknown angles for the following two triangles.

Answer:
Sum of three angles = 180°
Triangle 1:
30° + 60° + x = 180
90° + x° = 180°
x° = 180° – 90°
x° = 90°
Triangle 2:
45° + 20° + y = 180°
65° + y = 180°
y = 180° – 65°
y = 115°

Question 8.
If an exterior angle of a triangle has a measure of 35°, what is the measure of the adjacent interior angle?
Answer:
35° + x = 180°
x = 180 – 35
x = 145°
Thus the measure of the adjacent interior angle is 145°
Question 9.
Find the value of x.
x = ____
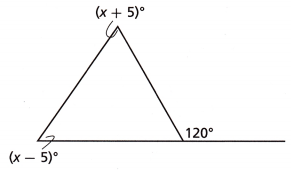
Answer:
120° + y = 180°
y = 180° – 120°
y = 60°
(x – 5)° + (x + 5)° + 60 = 180°
x – 5 + x + 5 + 60 = 180
2x + 60 = 180
2x = 180 – 60
2x = 120
x = 120/2 = 60
x = 60°
x – 5 = 60 – 5 = 55°
x + 5 = 60 + 5 = 65°
Question 10.
The measures of an exterior angle of a triangle and its adjacent interior angle add to what value?
A. 90°
B. 100°
C 180°
D. 360°
Answer: The measures of an exterior angle of a triangle and its adjacent interior angle is equal to 180 degrees.
So, option C is the correct answer.
Question 11.
The measure of an exterior angle of a triangle and the sum of the measures of the two remote interior angles are _____________
Answer: The measure of an exterior angle of a triangle and the sum of the measures of the two remote interior angles are 180 degrees.
Spiral Review
Question 12.
Hayden and Jamie completed 20 math problems together. Jamie completed 2 more than twice the number that Hayden completed. Let p represent the number of math problems Hayden completed. Write an equation that can be used to find the number of math problems that Jamie completed.
Answer:
Let p represent the number of Math problems Hayden completed.
Let 2p+2 represent the number of Math problems Jamie completed.
2p + 2 + p = 20
3p + 2 = 20
3p = 20 – 2
3p = 18
p = 18/3 = 6
p = 6
Thus Hayden completed 6 math problems.
2p + 2 = 2(6) + 2 = 12 + 2 = 14
Thus Jamie completed 14 Math problems.
Question 13.
Does the equation 5(x – 3) = 10x – 15 have one solution, infinitely many solutions, or no solution?
Answer:
5(x – 3) = 10x – 15
5x – 15 = 10x – 15
5x – 10x = 15 – 15
-5x = 0
x = 0
Thus x = 0 has infinite number of solutions.
Question 14.
Find the value of x, given that 4(3x + 2) = 44.
Answer:
Given,
4(3x + 2) = 44
12x + 8 = 44
12x = 44 – 8
12x = 36
x = 36/12
x = 3