We included HMH Into Math Grade 8 Answer Key PDF Module 2 Review to make students experts in learning maths.
HMH Into Math Grade 8 Module 2 Review Answer Key
Vocabulary
center of dilation
congruent
enlargement
reduction
similar
transformation
translation
Tell whether each statement is true or false. If it is false, correct the underlined word to make the statement true.
Question 1.
The image of dilation is always congruent to the preimage. _________
Answer: True
For a dilation, corresponding angles of the image and preimage are congruent. True, because the image and preimage are congruent, so the corresponding angles are congruent. O B. False, because the image and preimage are congruent, so the corresponding angles are similar.
Question 2.
The preimage of a reduction is larger than the image. _________
Answer: True
That’s because, in a reduction, you’re mapping multiple inputs to a single output.
– An enlargement has a scale factor greater than 1 and the image has a long distance from the point of dilation than the pre-image. A reduction has a scale factor between 0 and 1 and shrinks on the coordinate plane.
Question 3.
Lines through each pair of corresponding vertices in a dilation intersect at the centre of dilation. ___________
Answer: True
The centre of dilation can be anywhere on the coordinate plane as long as the lines that connect each pair of corresponding vertices between the original and dilated image intersect at the centre of dilation.
Question 4.
A dilation is a type of translation that enlarges or reduces a figure. ___________
Answer: The given statement is true.
Dilation is a transformation, which is used to resize the object. Dilation is used to make the objects larger or smaller. This transformation produces an image that is the same as the original shape.
Concepts and Skills
Question 5.
Use Tools Triangle R’S’T is a dilation of Triangle RST. What is the scale factor of the dilation? State what strategy and tool you will use to answer the equation, explain your choice, and then find the answer.
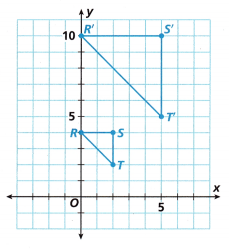
Answer:
You can go for calculating the scale factor with the help of the following formula:
Scale factor = scaled size/real size
real size = 5
scaled size = 2
scale factor = 5/2 = 2.5
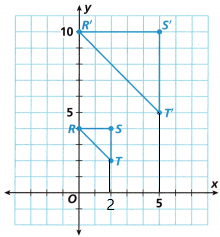
Question 6.
Select the sequence of transformations that results in figures that are similar but not congruent.
A. 180° rotation, dilation with a factor of \(\frac{1}{4}\)
B. translation 3 units up, 90° clockwise rotation
C. reflection across the x-axis, translation 6 units right
D. 90° counterclockwise rotation, reflection across the y-axis
Answer:
Question 7.
Are Triangles GHJ and LMN similar? Explain your reasoning.
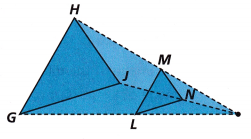
Answer:
Both are similar.
Reason:
When the size of a shape is increased or reduced then the image of the shape will be similar to the pre-image. The similar figures have dimensions equal in proportion.
Draw the image of each dilation in the coordinate plane. The centre of each dilation is the origin.
Question 8.
Triangle ABC is dilated by a scale factor of 3 to form Triangle A’B’C’.
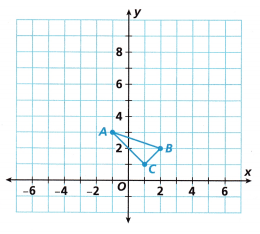
Answer:
Dilation is a transformation, which is used to resize the object. Dilation is used to make the objects larger or smaller. This transformation produces an image that is the same as the original shape. But there is a difference in the size of the shape. A dilation should either stretch or shrink the original shape. This transformation is expressed by the term scale factor.
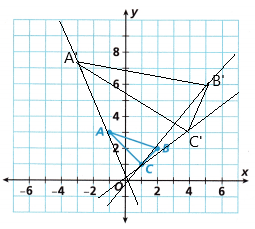
In the above figure, we can see, that the triangle ACB is transformed into a bigger triangle, i.e., A’B’C’ after the dilation process. Hence, it is the case of enlargement of the size of an object or shape.
Question 9.
Quadrilateral FGHJ is dilated by a scale factor of \(\frac{1}{2}\) to form Quadrilateral F’G’H’J’.
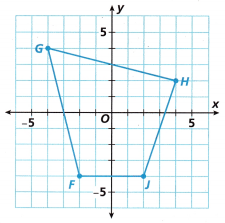
Answer:
Dilation is a transformation, which is used to resize the object. Dilation is used to make the objects larger or smaller. This transformation produces an image that is the same as the original shape. But there is a difference in the size of the shape. A dilation should either stretch or shrink the original shape. This transformation is expressed by the term scale factor.
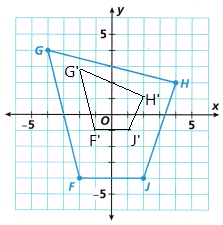
In the above figure, FGHJ is transformed into a small quadrilateral, i.e., F’G’H’J’ after the dilation process. Hence, it is the case of the reduction of the size of an object or shape.
Question 10.
Quadrilaterals LMNP and WXYZ are similar. Which sequence of transformations could be used to obtain Quadrilateral WXYZ from Quadrilateral LMNP?
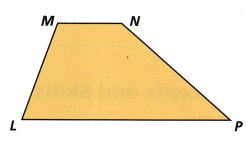
A. 180° rotation, dilation
B. vertical translation, dilation
C. dilation, reflection across a horizontal line
D. reflection across a horizontal line, vertical translation
Answer:
Options C and D
– This type of translation is called reflection because it flips the object across a line by keeping its shape or size constant.
– This type of translation expands or contracts the object by keeping its orientation or shape the same. This is also known as resizing
Question 11.
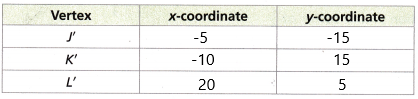
Triangle JKL has vertices 7(-1, -3), K(-2, 3), and L(4, 1). It is dilated by a scale factor of 5, with the origin as the centre of dilation, to produce Triangle J’K’L’. Complete the table with the coordinates of the vertices of the image of the dilation.

Answer:
Dilating points on a coordinate plane with a centre of dilation at the origin is fairly easy; just multiply its x– and y-coordinates by the scale factor.
Dilating points on a coordinate plane with a centre of dilation at the origin is fairly easy; just multiply its x– and y-coordinates by the scale factor.
J’ = (5(-1), 5(-3)) = (-5, -15)
K’ = (5(-2), 5(3)) = (-10, 15)
L’ = (5(4), 5(1)) = (20, 5)
Question 12.
Triangle DEF has vertices D(-4, 0), E( 1, 3), and F(3, -4). It is dilated by a scale factor of \(\frac{3}{4}\), with the centre of dilation at the origin. Use words from the box to complete the sentences about the dilation.
The image of the dilation is _____ than the preimage. The image of Vertex D is on the ___. The image of Vertex F has a ____ x-coordinate.

Answer:
The centre of dilation is a fixed point in the plane. Based on the scale factor and the centre of dilation, the dilation transformation is defined. If the scale factor is more than 1, then the image stretches. If the scale factor is between 0 and 1, then the image shrinks.
The given vertices:
D(-4, 0), E( 1, 3), and F(3, -4)
Dilating points on a coordinate plane with a centre of dilation at the origin is fairly easy; just multiply its x– and y-coordinates by the scale factor.
Given scale factor = 3/4
D’ = (3/4(-4), 3/4(0)) = (3, 0)
E’ = (3/4(1), 3/4(3)) = (3/4, 9/4)
F’ = (3/4(3), 3/4(-4)) = (9/4, 3)
The image of the dilation is smaller than the preimage. The image of Vertex D is on the x-axis. The image of Vertex F has a positive x-coordinate.