We included HMH Into Math Grade 8 Answer Key PDF Module 2 Lesson 3 Understand and Recognize Similar Figures to make students experts in learning maths.
HMH Into Math Grade 8 Module 2 Lesson 3 Answer Key Understand and Recognize Similar Figures
I Can describe a sequence of transformations that exhibits the similarity between two figures.
Spark Your Learning
To make a design for a phone case, start with Parallelogram ABCD. Then dilate the parallelogram using a vertex as the centre of dilation. Finally, translate the dilated parallelogram. Draw a possible final image for the figure and label it A’B’C’D’. Show your work.


How are the sides and angles of ABCD and A’B’C’D’ the same? How are they different?
Turn and Talk Use the same translation first, followed by the same dilation. Would the answers to the above questions be different? Explain.
Build Understanding
1. Use the shapes shown to make a customized phone case.
Connect to Vocabulary
Two figures are similar if one can be obtained from the other by a transformation or sequence of transformations that may include a dilation.
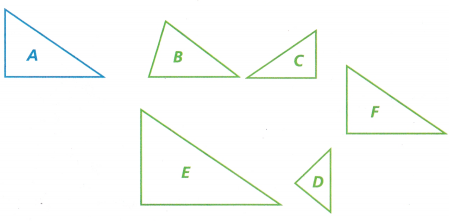
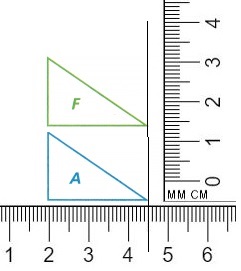
A. Which triangles are similar to Triangle A? You can use tracing paper, a protractor, and/or a ruler to help you decide which triangles are similar.
_________________
Answer:
Triangle A is similar to Triangle F.
Explanation:
By using a protractor, and/or a ruler triangle A and F are similar as shown below.
B. For each of the similar triangles you identified, describe a transformation or sequence of transformations that take Triangle A to the other triangle.
Answer:
Triangle A is congruent to Triangle F.
Explanation:
A transformation is the movement of a figure.
There are four types of transformations:
(i)Reflection,
(ii) Rotation,
(iii) Translation,
(iv) Dilation.
A transformation can either be a congruent or similar shape to the original image.
Congruent means that the shape or figure retains its size, shape, length, and angles of the original shape. Rotations, reflections, and translations give congruent figures.
They have the exact shape but they can turned, slid, or flipped.
A similar shape is a shape that is has been resized.
It has the same corresponding angle measurements but the side lengths are different.
To keep a shape similar, the sides must be in proportion with each other,
which means that they are growing or shrinking at the same rate.
Since, similar shapes have the same angle measurements and have proportional side lengths,
the missing angles and side lengths can be found from one shape to the other.
Dilations result in similar shapes.
C. Is Triangle A similar to Triangle B? Why or why not?
Answer:
No,
Triangle A is not similar to triangle B.
Explanation:
By measuring with tools, both the triangles are not matching.
D. Add another triangle to your design. Dilate Triangle B using a scale factor of 1 and then rotate the image to form Triangle G. How are Triangle B and Triangle G related? Explain.
Answer:
Dilate Triangle B using a scale factor of 1 and then rotate the image to form Triangle G,
for a scale factor of 1 there will be no change in the shape and size of the figure.
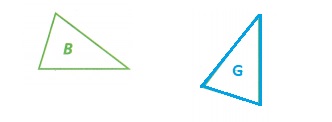
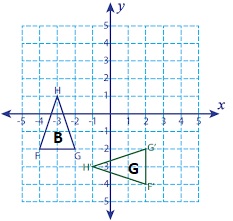
Triangle B is called pre image and triangle G is called image.
Explanation:
The pre-image is the initial figure or original shape.
The image is the figure after the transformation and on a graph.
A rotation is a turn around a center point.
In a rotation, the distance from each point on the shape to the center remains the same.
A rotation is identified by a shape turning a specific amount degrees, usually 90, 180, or 270 degrees,
around a point either clockwise or counterclockwise.
This means with each rotation performed four things are given.
First the shape, then the direction of rotation, which is clockwise or counterclockwise,
followed by the degree of turn and the point of rotation which is commonly the origin of a graph.
Turn and Talk If two figures are congruent can you always conclude that they are similar? Why or why not?
Answer:
Yes, Similar figures are always congruent, whereas the congruent figures are not necessarily similar.
Explanation:
Two triangles are said to be congruent if all three corresponding sides are equal,
and all the three corresponding angles are equal in measure.
These triangles can be slides, rotated, flipped and turned to be looked identical.
If repositioned, they coincide with each other. The symbol of congruence is’ ≅’.
The meaning of congruence in Maths is when two figures are similar to each other,
based on their shape and size.
Step It Out
2. Use a coordinate plane to draw figures for a custom phone case. Include several similar figures in the design, as shown on the graph.
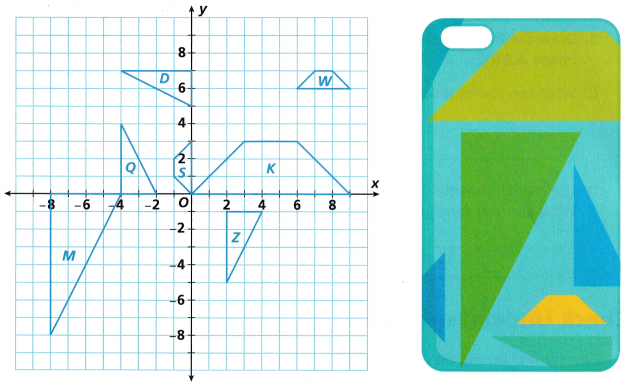
A. For each pair of similar figures, describe a sequence of transformations that can be used to map the first figure to the second figure.
Figure K to Figure W
Answer:
Figure K is dilated to figure W, with dilation scale factor k = \(\frac{1}{3}\)
Polygon K with co ordinates ABCD is changed to P’Q’R’S’
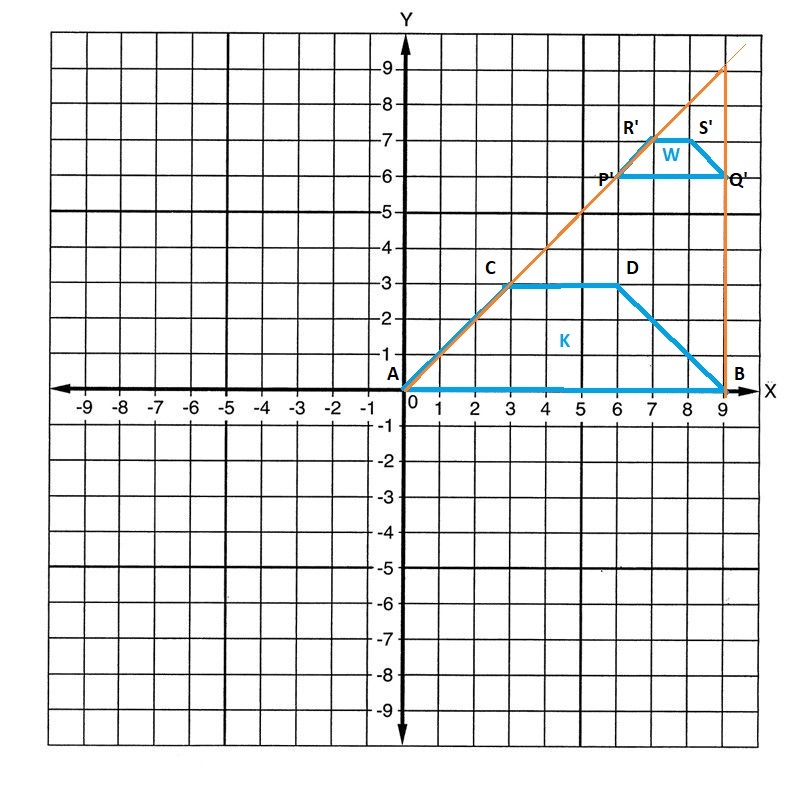
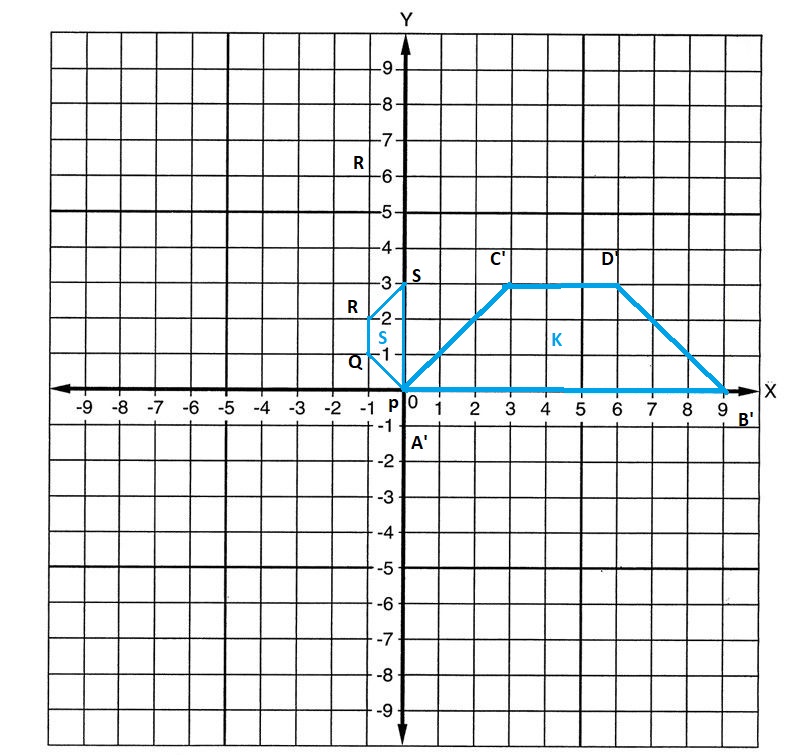
Figure S to Figure K
Explanation:
Figure S is dilated to figure K, with dilation scale factor k = 3
Polygon S with co ordinates PQRS is changed to A’B’C’D’ with multiplication of 3,
and rotate clock wise to 90 degrees right side, as shown below figure.
B. Which pair of similar figures can be mapped from one to the other by the given sequence of transformations?
a dilation with scale factor \(\frac{1}{2}\) and center of dilation (0, 0), followed by a reflection across the x-axis
Answer:
Reflection and dilation is the sequence of transformation.
Figure Q to Figure M.
Explanation:
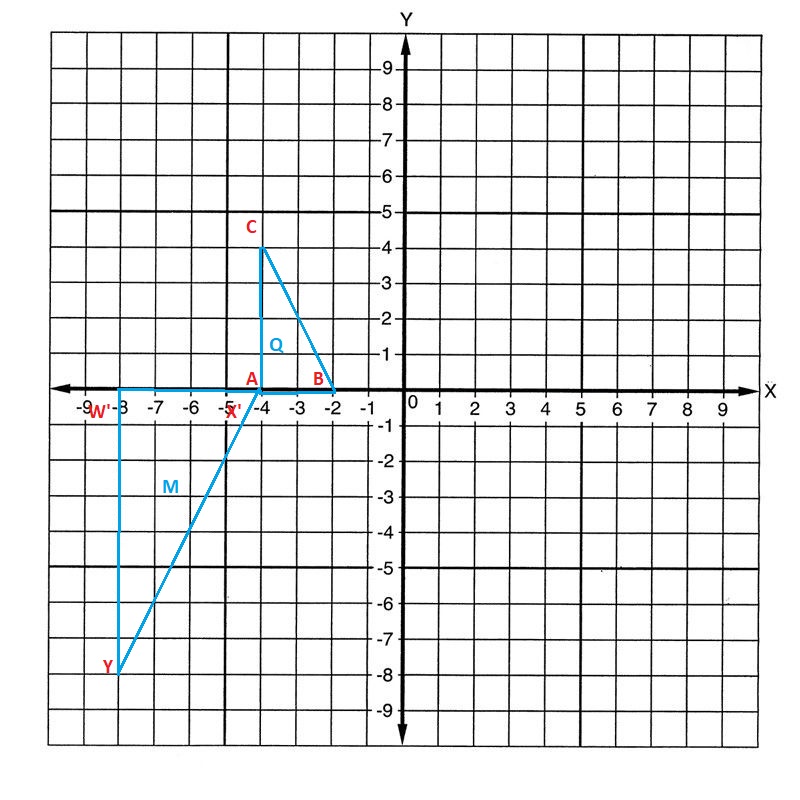
The dilation (x, y) → (2x, 2y) with a center of dilation (0, 0)
followed by a translation 12 units left and 2 units up.
(x, y) → (2x, 2y)
A(-4, 0) → (2x, 2y) = W(-8, 0)
B(-2, 0) → (2x, 2y) = X(-4, 0)
C(-4, 4) → (2x, 2y) = Y(-8, 8)
3. For the phone case, make an additional shape ∆ABC. Dilate the triangle using a dilation with a scale factor of \(\frac{1}{2}\) and center of dilation (0, 0). Then reflect the image across the y-axis.
A. Draw the image of ∆ABC after the dilation.
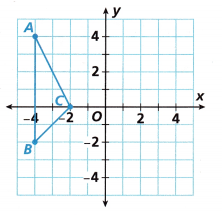
Answer:

Explanation:
The rule for a reflection over the y -axis is (x,y)→(−x,y)
(x,y)→(−kx, ky)
k = \(\frac{1}{2}\)
A(-4, 4) → A'(-x/2, y/2) = A'(2, 2)
B(-4, -2) → B'(-x/2, y/2)= B'(2, -1)
C(-2, 0) → C'(-x/2, y/2) = C'(1, 0)
B. Draw the final image after the reflection. Label the final image ∆A’B’C’.
Answer:
Reflection and Dilation transformation with a scale factor \(\frac{1}{k}\),
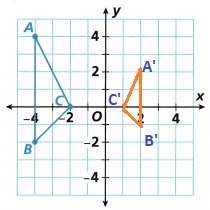
Explanation:
A reflection is a transformation that flips a figure across a line.
Dilation is a process of changing the size of an object or shape by decreasing or increasing its dimensions.
Dilation transformation with a scale factor \(\frac{1}{k}\) is used.
C. What can you conclude about ∆ABC and ∆A’B’C’? Why?
Answer:
∆ABC and ∆A’B’C’ is reduced to half its original image.
A dilation is a reduction if the scale factor is between 0 and 1.
Explanation:
Reduction is a transformation of an object that has the same shape,
but decreases in size of the object.
Due to the scale factor \(\frac{1}{2}\),
the image is reduced to \(\frac{1}{2}\) and,
the image is formed at right hand side of the y – axis as shown in the above figure.
D. Use a dilation with a scale factor of 1 instead of a scale factor of \(\frac{1}{2}\).
What can you conclude about ∆ABC and ∆A’B’C’ in this case? Explain.
Answer:
In case of ∆ABC and ∆A’B’C’ is equivalent and result in the same size and shape.
Explanation:
The rule for a reflection over the y -axis is (x, y)→(−x, y)
(x,y)→(−kx, ky)
a dilation with a scale factor of 1 instead of a scale factor of \(\frac{1}{2}\).
k = 1
A(-4, 4) → A'(-x, y) =A'(4, 4)
B(-4, -2) → B'(-x, y)=B'(4, -2)
C(-2, 0) → C'(-x, y) =C'(2, 0)
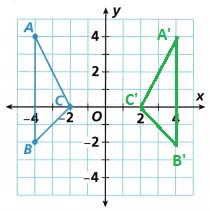
Check Understanding
Question 1.
Doretta is choosing tiles for a mosaic in a kitchen. She wants to choose two tiles that are similar but not congruent. Which pair of tiles could she use? Explain why she can choose only those tiles.

Answer:
Tile A and D two are similar but not congruent.
Explanation:
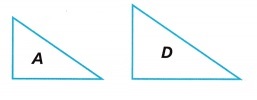
Tile A and D, two tiles that are similar but not congruent.
the size of the tile A and D are different but the shape is same.
Question 2.
Identify all pairs of similar figures on the coordinate plane. For each pair, describe the sequence of transformations that maps one figure to the other.
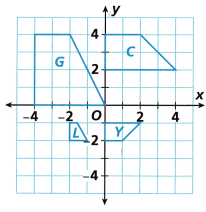
Answer:
Figure G and figure C are similar pairs.
with a reduction scale factor \(\frac{1}{2}\) and rotation 90 degrees clock wise.
Explanation:
Figure G is transformed to figure C and the sequence of transformations that maps one figure to the other.
The figure C is reduced by a scale factor of \(\frac{1}{2}\).
Figure G(x, y) co ordinates are changed as Figure C (x/2, y/2)
To rotate the figure 90 degrees clockwise about a point,
every point(x, y) will rotate to (y, -x).
Let’s understand the rotation of 90 degrees clockwise about a point visually.
So, each point has to be rotated and new coordinates have to be found.
On Your Own
Question 3.
Ryan is a landscape architect. He uses the coordinate plane shown to design flower beds at a mail.
A. To draw flower bed B, Ryan reflects flower bed A across the x-axis. Then he applies the dilation
(x, y) → (2x, 2y). Draw and label flower bed B.
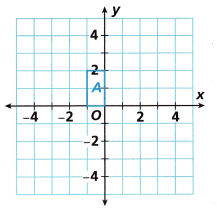
Answer:
The dilation (x, y) → (2x, 2y)
Explanation:
When we reflect a point across the x-axis, the x-coordinate remains the same,
but the y-coordinate is taken to be the additive inverse.
The reflection of point (x, y) across the x-axis is (x, -y).
The dilation scale factor (x, y) → (2x, 2y).
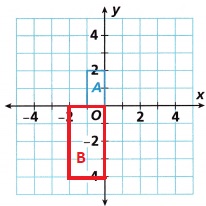
B. To draw flower bed C, Ryan rotates flower bed A by 180° about the origin. Then he applies the dilation (x, y) → (2.5x, 2.5y). Draw and label flower bed C.
Answer:
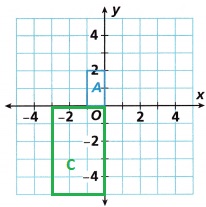
Explanation:
The rule for a rotation by 180° about the origin is (x,y)→(−x,−y),
then the reflection over x axis is same.
The dilation (x, y) → (2.5x, 2.5y).
C. What can you conclude about the three flower beds?
Answer:
The size of the three beds are increasing size by dilation factor.
The formation for image is below that x axis as shown in the above figures.
Question 4.
Art A car show has advertising posters in different shapes and sizes. They are shown as they appear next to each other on a wall at the car show.

A. Circle all of the posters that are similar.
Answer:

Explanation:
The car show blue and purple color advertising posters are similar to each other with a reduction,
a dilation with a scale factor of \(\frac{1}{2}\).
B. For the posters you identified, describe a sequence of transformations that takes one poster to the other.
Answer:
Dilation reduction transformation.
Explanation:
Dilation are transformations that generate an enlargement or a reduction.
Here the reduction of size was the transformation takes place.
Translations are congruence transformations that move an object,
without changing its size or shape.
Use the graph to solve Problems 5-7.
Question 5.
Which pair of similar triangles can be mapped from one to the other by a dilation with scale factor \(\frac{1}{3}\) and center of dilation (0, 0), followed by a rotation of 180° clockwise around the origin?
Answer:
Triangles P and J are similar triangles.
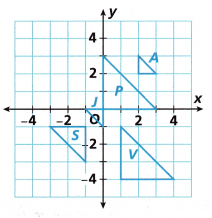
Explanation:
Triangle P and J are pair of similar triangles can be mapped from one to the other,
by a dilation with scale factor \(\frac{1}{3}\) and center of dilation (0, 0),
followed by a rotation of 180° clockwise around the origin.
Question 6.
Which pair of similar triangles can be mapped from one to the other by a dilation with scale factor 3 and center of dilation (0, 0), followed by the translation (x, y) → (x – 6, y – 6)?
Answer:
Triangle A and P.
Explanation:

Explanation:
A pair of similar triangles can be mapped from one to the other by a dilation with scale factor 3,
and center of dilation (0, 0), followed by the translation (x, y) → (x – 6, y – 6).
Triangle A co ordinates, (x, y) → (x – 6, y – 6).
with scale factor 3,
k = 3
(2, 3) → (3x – 6, 3y – 6) → (6 – 6, 9 – 6) → (0, 3)
(2, 2)→ (3x – 6, 3y – 6) → (6 – 6, 6 – 6) → (0, 0)
(3, 2)→ (3x – 6, 3y – 6) → (9 – 6, 6 – 6) → (3, 0)
Question 7.
Describe a sequence of transformations that can be used to map Triangle J to Triangle S.
Answer:
Transformation from Triangle J to Triangle S is reduction transformation.
Explanation:
A transformation is a change in the position, size, or shape of a new geometric figure.
Co-ordinates of J are, (0, 0), (-1, 0) and (0, -1)
Co-ordinates of S are, (-1, -1), (-3, -1) and (-1, -3)
Pair of similar triangles can be mapped from one to the other by a dilation with scale factor 2,
and center of dilation (0, 0), followed by the translation (x, y) → (2x, 2y).
Triangle S is shifted down and then to left one unit.

Question 8.
Glass laboratory flasks come in a variety of shapes and sizes. Different flasks have different purposes, such as heating, measuring, and mixing. Are any of the flasks shown similar? Explain why or why not.

Answer:
No, the flasks are not similar.
Explanation:
The flasks which are shown above are different shape and volume,
two are different flasks have different purposes.
Such as heating, measuring, and mixing and not similar flasks.
Question 9.
Describe a sequence of transformations that can be used to map ∆RST with vertices R(-1, 0), S(0, 1), and T(1, 0) to ∆JKL with vertices J(-4, 0), K(0, -4), and L(4, 0).
Answer:
Dilation and rotation transformation.
Explanation:
∆RST with vertices R(-1, 0), S(0, 1), and T(1, 0) to ∆JKL with vertices J(-4, 0), K(0, -4), and L(4, 0).
When rotating a point 180 degrees counter clockwise about the origin,
our point A(x,y) becomes A'(-x,-y). So all we do is make both x and y negative.
dilation scale factor k = 4
(x, y) → (-kx, -ky)
k = 4
R(-1, 0) → (-4 x -1, -4 x 0) = J(-4, 0)
S(0, 1) → (-4 x 0, -4 x 1) = K(0, -4)
T(1, 0) → (-4 x 1, -4 x 0) = L(-4, 0)
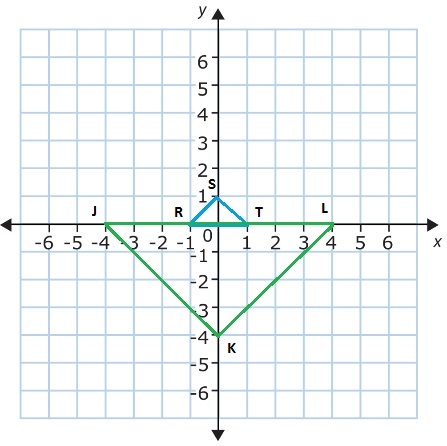
Question 10.
Open Ended The coordinates of the vertices of ∆ABC are A(0, 0), 8(0, 4), and C(-2, 0). Give the coordinates of the vertices of a triangle, ∆DEF, that is similar to ∆ABC but not congruent to ∆ABC. Then describe a sequence of transformations that maps ∆ABC to ∆DEF.
Answer:
Dilation transformation with a scale factor ‘k’
Explanation:
∆DEF, that is similar to ∆ABC but not congruent to ∆ABC.
∆DEF and ∆ABC are same with different size.
Question 11.
Use Repeated Reasoning Jaycee draws a sequence of squares on the coordinate plane. First she draws the square shown and dilates it using (x, y) → (3x, 3y). Then she uses this same transformation to dilate the image. She continues dilating each image in this way to draw a total of six squares. What dilation could she use to map the first square she draws directly to the last square she draws?
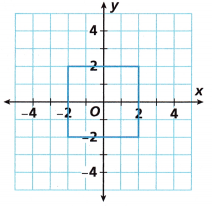
Answer:
Dilates it by using (x, y) → (3x, 3y).
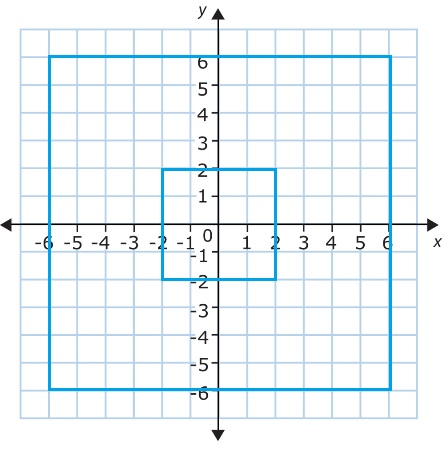
Explanation:
Dilation by a scale factor k,
k = 3
Given, (x, y) → (3x, 3y).
x = -2; y = 2
x, y co-ordinates of an enlarged figure are,
(-2, 0) → (-6, 0).
(0, 2) → (0, 6).
(2, 0) → (6, 0).
(0, -2) → (0, -6).
Question 12.
If Figure X is similar to Figure Y, and Figure Y is similar to Figure Z, can you conclude that Figure X is similar to Figure Z? Explain.
Answer:
YES,
Explanation:
Figure X is similar to Figure Y, and Figure Y is similar to Figure Z.
Figure X is similar to Figure Z and are congruent figures.
I’m in a Learning Mindset!
Do I have a fixed-mindset voice or a growth-mindset voice in my head when I’m working with finding similar figures? How can I tap into my growth-mindset voice?
Answer:
Yes, Answer may vary.
Explanation:
I have a fixed-mindset voice or a growth-mindset voice in my head,
when I’m working with finding similar figures.
Growth Mindset in Maths is an approach to teaching mathematics,
which believes that mindset is more important than initial ability,
in determining the progress made by pupils in their mathematical understanding.
Pupils with a growth mindset will make better progress than pupils with a fixed mindset.
Lesson 2.3 More Practice/Homework
Understand and Recognize Similar Figures
Question 1.
Use Tools Use a coordinate plane to design the background image for a video game. Start with ∆ABC.
A. To draw ∆DEF, translate ∆ABC using
(x, y) → (x – 2, y). Then apply a dilation with scale factor 2 and center of dilation (0, 0). Draw and label ∆DEF.
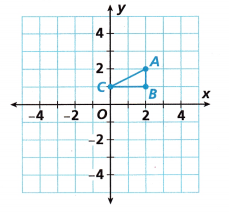
Answer:
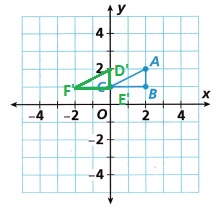
Explanation:
Given, (x, y) → (x – 2, y).
Then apply a dilation with scale factor 2 and center of dilation (0, 0).
A(2, 2) → (2 – 2, 2) = D'(0, 2)
B(2, 1) → (2 – 2, 1) = E'(0, 1)
C(0, 1) → (0 – 2, 1) = F'(-2, 1)
B. To draw ∆GHJ, reflect ∆ABC using
(x, y) → (x, -y). Then apply a dilation with scale factor 2 and center of dilation (0, 0).
Draw and label →GHJ.
Answer:
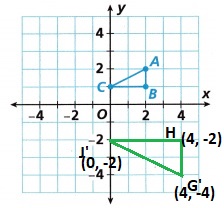
Explanation:
Given, (x, y) → (x, -y).
Then apply a dilation with scale factor 2 and center of dilation (0, 0).
A(2, 2) → (2×2, -2×2) = G'(4, -4)
B(2, 1) → (2×2, -1×2) = H'(4, -2)
C(0, 1) → (0x2, -2×1) = J'(0, -2)
C. Critique Reasoning A student claims that all three triangles are similar. Do you agree or disagree? Explain.
Answer:
YES,
Explanation:
All three triangles are similar triangles,
triangle ABC and DEF are similar.
when shifted to left triangle GHJ is a similar triangle with enlarged dilation scale factor 2.
Question 2.
A designer is trying different designs for a business logo. Several of the logos are shown?.
A. Circle all of the logos that are similar to each other.
Answer:
B. For the logos you identified, describe a sequence of transformations that takes one logo to the other.
Answer:
Question 3.
Math on the Spot Consider the pairs of figures on the coordinate planes.
A. Identify a sequence of transformations that will transform Figure A onto Figure B. Tell whether the figures are congruent. Tell whether they are similar.
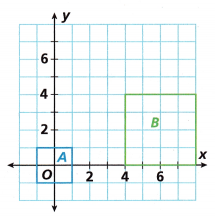
Answer:
Translation and dilation with a scale factor 2 is the sequence of transformation.
(x, y) (kx, ky)
k = 2
Explanation:
Figure A is shifted 6 units right,
enlarged the figure with an enlarging scale factor k = 2,
then shifting the figure A to 2 units up to form figure B.
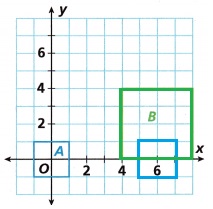
B. Identify a sequence of transformations that will transform Figure C onto Figure D. Tell whether the figures are congruent. Tell whether they are similar.
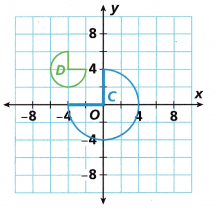
Answer:
A rotation followed by a dilation of enlargement.
Explanation:
Rotation means the circular movement of an object around a center.
It is possible to rotate different shapes by an angle around the center point.
Rotation from Figure C to Figure D .
The sequence of transformations are a rotation followed by a rotation can be used to,
map Figure M to Figure N.
Test Prep
Question 4.
Figure M and Figure N are similar triangles. Which sequence of transformations can be used to map Figure M to Figure N?
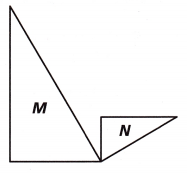
A. a dilation followed by a reflection
B. a rotation followed by a dilation
C. a translation followed by a rotation
D. a dilation followed by a translation
Answer:
Option (B) a rotation followed by a dilation.
Explanation:
Rotation means the circular movement of an object around a center.
It is possible to rotate different shapes by an angle around the center point.
Rotation followed by dilation from Figure M and Figure N are similar triangles.
Question 5.
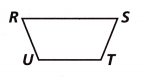
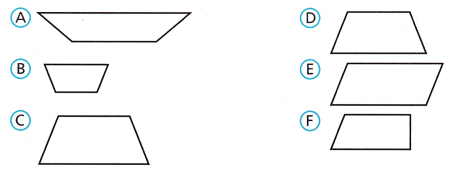
Select all of the figures that are similar to Trapezoid RSTU.
Answer:
Figure C and D are similar, but 180 degrees rotated with x axis.
Explanation:
A trapezoid is a four-sided closed 2D shape that has an area and a perimeter.
A rotation is a transformation that turns a figure about a point.
Question 6.
Maria draws ∆PQR. Then she applies a dilation with scale factor \(\frac{1}{3}\) and center of dilation P to the triangle. Next, she translates the image 2 centimeters up and 3 centimeters right. She labels the final image as ∆XYZ. Which of the following must be true about ∆PQR and ∆XVZ?
A. ∆PQR and ∆XYZ are congruent and similar.
B. ∆PQR and ∆XYZ are congruent but not similar.
C. ∆PQR and ∆XYZ are similar but not congruent.
D. ∆PQR and ∆XYZ are neither similar nor congruent.
Answer:
Option (C) is correct.
Explanation:
Similar means that the figures have the same shape, but not the same size.
Similar figures are not congruent.
These two triangles are similar.
They are the same shape, but they are not the same size.
∆PQR and ∆XYZ are similar but not congruent.
they are similar due to the shifting the figure by 2 centimeters up and 3 centimeters right.
Due to the dilation scale factor of reduction of the resultant figure,
∆XYZ is smaller then the original figure ∆ABC.
Spiral Review
Use the graph shown to answer Problems 7-8.
Question 7.
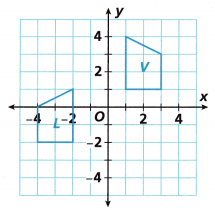
Make a figure that is congruent to Figure V by reflecting Figure V across the x-axis and then translating the image 1 unit right. Draw this figure and label it Figure F.
Answer:
Explanation:
Two geometric figures are said to be congruent, or to be in the relation of congruence,
if it is possible to superpose one of them on the other so that they coincide throughout.
By reflecting Figure V across the x-axis and then translating the image 1 unit right,
the result is Figure F.
Question 8.
Are Figure V and Figure L congruent? Explain why or why not.
Answer:
Yes, Figure V and Figure L congruent.
Explanation:
Figure V is shifted 3 units left and 3 units down.
When the figure is turn left the result is figure L.
Question 9.
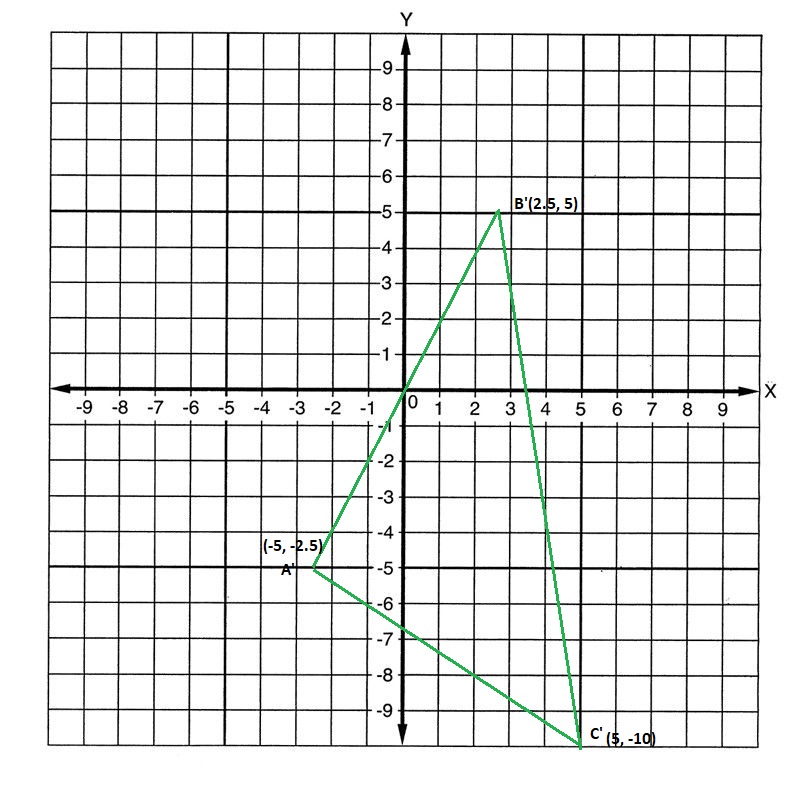
∆ABC has vertices A(-2, -1), B(1, 2), and C( 2, -4). If ∆A’B’C’ is a dilation of ∆ABC with a scale factor of 2.5 and center of dilation (0, 0), give the coordinates of the vertices of ∆A’B’C.
Answer:
A(-2, -1) → (-2×2.5, -1×2.5) = A'(-5, -2.5)
B(1, 2) → (1×2.5, 2×2.5) = B'(2.5, 5)
C(2, -4) → (2×2.5, -4×2.5) = C'(5, -10)
Explanation:
Given, (x, y) → (kx, ky).
Then apply a dilation with scale factor 2.5 and center of dilation (0, 0).
∆ABC has vertices A(-2, -1), B(1, 2), and C( 2, -4).
If ∆A’B’C’ is a dilation of ∆ABC with a scale factor of 2.5 and center of dilation (0, 0),
the coordinates of the vertices of ∆A’B’C are,
A(-2, -1) → (-2×2.5, -1×2.5) = A'(-5, -2.5)
B(1, 2) → (1×2.5, 2×2.5) = B'(2.5, 5)
C(2, -4) → (2×2.5, -4×2.5) = C'(5, -10)