Into Math Grade 8 Module 2 Lesson 2 Answer Key Explore Dilations

We included HMH Into Math Grade 8 Answer Key PDF Module 2 Lesson 2 Explore Dilations to make students experts in learning maths.

HMH Into Math Grade 8 Module 2 Lesson 2 Answer Key Explore Dilations

I Can identify and perform dilations given a scale factor and center of dilation, perform a dilation on a coordinate plane, and identify an algebraic rule for the dilation.

Spark Your Learning
On a computer, Raquel uses polygons and a circle to make a model of the top of London’s Big Ben clock tower. Then she reduces it.


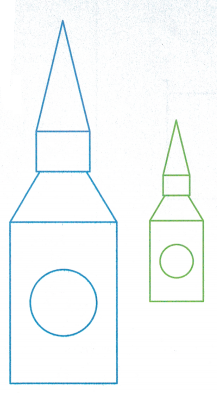
Compare Raquel’s image and reduction. What do you find?

Turn and Talk What is the relationship between the perimeter of Raquel’s original image and her reduction? How does this relate to the relationship between the side lengths?

Build Understanding

1. Rectangle R’S’T’U’ is a dilation of Rectangle RSTU.

Connect to Vocabulary
A dilation is a transformation that produces an image that is proportional to its preimage.

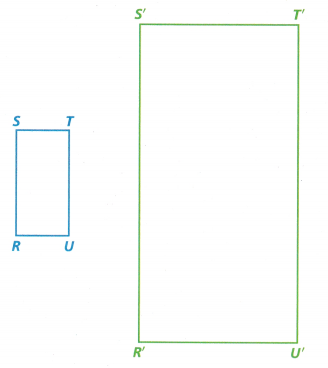
A. Measure the sides of the figures, then fill in the table.

What is the relationship between the measurements of the rectangles?
Answer:

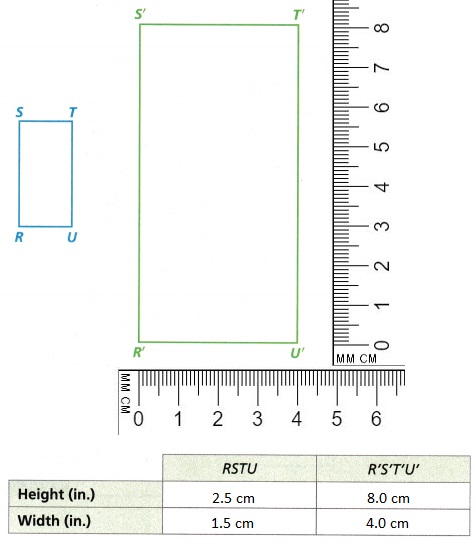
Explanation:
The relationship between the measurements of the rectangles are,
the perimeter of rectangle R’S’T’U’ and rectangle RSTU.
P = 2(length + width)
P = 2(2.5+1.5)
P = 8 cm for rectangle RSTU preimage,
P = 2(8.0 + 4.0)
P = 24 cm for rectangle R’S’T’U’ image.
The relationship between the measurements of the rectangles is,
the perimeter increased to 3 times for preimage.

B. What is the scale factor of this dilation?
___________________
Answer:
Scale factor is 3.
Dilation means changing the size of an object without changing its shape.
The size of the object may be increased or decreased based on the scale factor.
Scale Factor is defined as the ratio of the size of the new image to the size of the old image.

Explanation:
Scale factor is a number by which the size of any geometrical figure or shape,
which can be changed with respect to its original size.
It is the ratio of the sizes of the original figure with the dilated figure.
The scale factor can be denoted by r or k.
The image is enlarged if the scale factor is more than 1 (k > 1).
The image is contracted if the scale factor is less than 1 (0< k <1).
The image remains the same if the scale factor is 1 (k = 1).
The scale factor is a measure for similar figures,
who look the same but have different scales or measures.
The center of dilation is a fixed point in the plane.
Based on the scale factor and the center of dilation,
thus the dilation transformation is defined.

C. Points R and R’ are an example of corresponding vertices. Use a ruler or straight edge to draw four rays, each extending from a vertex of the image to the corresponding vertex of the preimage, and continuing through to the left. What do you notice?
Answer:
All four rays are meeting at one point by extending,
from a vertex of the image to the corresponding vertex of the preimage.

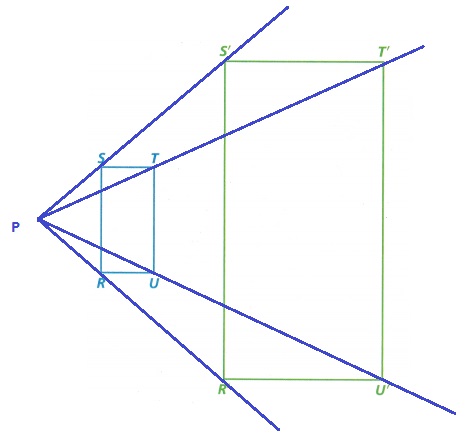
Explanation:
Points R and R’ are the corresponding vertices.
By using a ruler or straight edge we draw four rays,
each extending from a vertex of the image to the corresponding vertex of the preimage,
and continuing through to the left.
So, that all four rays are meeting at one point by extending.

Connect to Vocabulary
The scale factor of a dilation is the ratio of the side lengths of the image to the preimage. The point of intersection of lines through each pair of corresponding vertices in a dilation is called the center of dilation.

D. Label the center of dilation for Rectangles RSTU and R’S’T’U’ as Point P.

Explanation:
The center of dilation is a fixed point in the plane.
So, in the above figure shown the center of Dilation is ‘P’.

Step It Out

2.

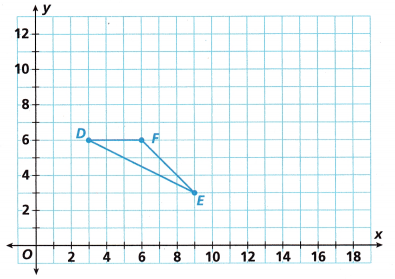
A. In order to dilate ∆DEF to form ∆D’E’F’ with a scale factor of 2 and center of dilation (0, 0), first draw a ray from the center of dilation through Vertex D.
Answer:

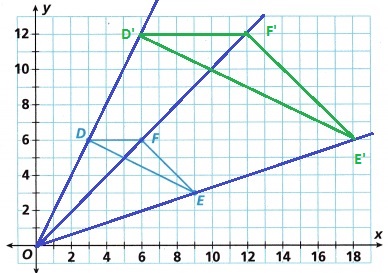
Explanation:
In the above figure,
ΔDEF is dilated (enlarged) to ΔD’E’F’ and the angles are the same.
The coordinates of the vertices of ΔDEF have been changed after dilation.
a scale factor of 2 and center of dilation
D(3, 6)  → D’ (6, 12)
E(9, 3)  → E’ (18, 6)
F(6, 6)  → F’ (12, 12)

B. Find a point on the ray that is twice the distance from the center of dilation as Vertex D. Label it D’.
Answer:
D(3, 6)  → D’ (6, 12)
Explanation:
ΔDEF is dilated (enlarged) to ΔD’E’F’ and the angles are the same.
The coordinates of the vertices of ΔDEF have been changed after dilation.
a scale factor of 2 and center of dilation
D(3, 6)  → D’ (6, 12)

C. Give the ordered pairs for Vertices D and D’. How are these values related to the scale factor?
Answer:
D(3, 6)  → D’ (6, 12)
Explanation:
When a dilation in the coordinate plane has the origin as the center of dilation,
The points on the dilated image by multiplying the x- and y-coordinates of the original figure.
For scale factor k, the algebraic representation of the dilation is (x, y) → (kx, ky).
a scale factor of 2 and center of dilation.
kx
k = 2; x = (3, 6)
2 x 3  =  6
2 x 6 = 12
D(3, 6)  → D’ (6, 12)

D. Predict the ordered pairs for Vertices E’ and F’. Explain your reasoning.
Answer:
E(9, 3)  → E’ (18, 6)
F(6, 6)  → F’ (12, 12)
Explanation:
When a dilation in the coordinate plane has the origin as the center of dilation,
Find the points on the dilated image by multiplying the x- and y-coordinates of the original figure.
For scale factor k, the algebraic representation of the dilation is (x, y) → (kx, ky).
In the above figure,
ΔDEF is dilated (enlarged) to ΔD’E’F’ and the angles are the same.
The coordinates of the vertices of ΔDEF have been changed after dilation.
a scale factor of 2 and center of dilation
E(9, 3)  → E’ (18, 6)
F(6, 6)  → F’ (12, 12)

E. Draw ∆D’E’F’ on the graph. Use rays from the center of dilation to draw your dilation.
Answer:

Explanation:
The point from which a figure is dilated is called the center of dilation.
A center of dilation can be inside, on, or outside center of dilation of a figure.
Use a straightedge to draw rays from the center of dilation through each set of corresponding vertices of figures.
If the figures of dilations to each other, then you can draw rays,,
from the center of dilation through each pair of corresponding vertices.

F. Using the ordered pairs of ∆DEF, how would you make a dilation ∆D”E”F” with a scale factor of \(\frac{1}{3}\) and center (0, 0)?
Answer:
ΔDEF is dilated (enlarged) to ΔD’E’F’ and the angles are the same.

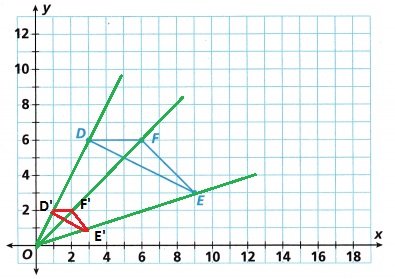
Explanation:
A scale factor of \(\frac{1}{3}\) and center (0, 0)
ΔDEF is dilated (enlarged) to ΔD’E’F’ and the angles are the same.
The coordinates of the vertices of ΔDEF have been changed after dilation.
A scale factor of \(\frac{1}{3}\) and center of dilation are,
D(3, 6)  → D’ (3/3, 6/3) = D'(1, 2)
E(9, 3)  → E’ (9/3, 3/3) = E'(3, 1)
F(6, 6)  → F’ (6/3, 6/3) = F'(2, 2)

G. Draw ∆D”E”F” on the graph. Use rays from the center of dilation to check your dilation. What are the coordinates of the vertices of ∆D”E”F”?
Answer:
D(3, 6)  → D’ (3/3, 6/3) = D'(1, 2)
E(9, 3)  → E’ (9/3, 3/3) = E'(3, 1)
F(6, 6)  → F’ (6/3, 6/3) = F'(2, 2)

Explanation:
The point from which a figure is dilated is called the center of dilation.
A center of dilation can be inside, on, or outside center of dilation of a figure.
Use a straightedge to draw rays from the center of dilation through each set of corresponding vertices of figures.
If the figures of dilations to each other, then you can draw rays,
from the center of dilation through each pair of corresponding vertices.

Turn and Talk What happens when you dilate ∆DFF with a scale factor of 1? Describe the resulting image.
Answer:

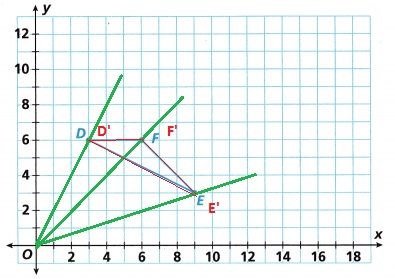
Explanation:
If the scale factor is more than 1, then the image stretches.
If the scale factor is between 0 and 1, then the image shrinks.
If the scale factor is 1, then the original image and the image produced are congruent,
both the images overlap each other, ∆DFF  and ∆D’E’F’ as shown in the above figure.

3. ∆G’H’J’ is a dilation of ∆GHJ. Find the scale factor and center of dilation. Represent the dilation algebraically.
A. Complete the table.

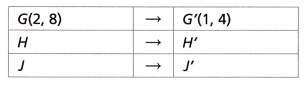
Answer:

Explanation:
(x, y) —> (kx, ky)
A scale factor of \(\frac{1}{2}\) and center of dilation.
A scale factor of \(\frac{1}{2}\) and center (0, 0)
ΔGJH is dilated (enlarged) to ΔG’J’H’ and the angles are the same.
The coordinates of the vertices of ΔGJH have been changed after dilation.
a scale factor of \(\frac{1}{2}\) and center of dilation
k is a scale factor
G(2, 8)  → G'(2/2, 8/2) = G'(1, 4)
H(10, 10)  → H'(10/2, 10/2) = H'(5, 5)
J(6, 2)  → J'(6/2, 2/2) = J'(3, 1)

B. How are the corresponding coordinates for the image and the preimage related?
Answer:

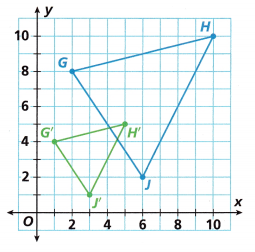
Explanation:
After a dilation, the pre-image and image have the same shape but not the same size.
In a dilation, the sides of the pre-image and the corresponding sides of the image are proportional.

C. What is the scale factor of the dilation?
Answer:
A scale factor of \(\frac{1}{2}\) and center of dilation.
Explanation:
Scale Factor is the ratio of the size of the new image to the size of the old image.
Based on the scale factor and the center of dilation, the dilation transformation is defined.
If the scale factor is more than 1, then the image stretches

D. Circle the algebraic representation that best describes this dilation. Explain your reasoning.
(x, y) → (x + \(\frac{1}{2}\), y + \(\frac{1}{2}\))           (x, y) → (x – \(\frac{1}{2}\), y – \(\frac{1}{2}\))
(x, y) → (\(\frac{1}{2}\)x, \(\frac{1}{2}\)y)                     (x, y) → (2x, 2y)
Answer:
(x, y) → (\(\frac{1}{2}\)x, \(\frac{1}{2}\)y)

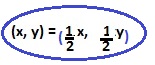
Explanation:
When a dilation in the coordinate plane has the origin as the center of dilation,
Find the points on the dilated image by multiplying the x- and y-coordinates of the original figure.
For scale factor k, the algebraic representation of the dilation is (x, y) → (kx, ky).
k = \(\frac{1}{2}\)
(x, y) → (\(\frac{1}{2}\)x, \(\frac{1}{2}\)y)

E. Draw rays through corresponding vertices of both figures to find the center of dilation. What is the center of dilation?
Answer:

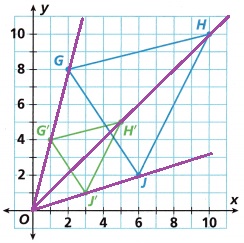
Explanation:
A scale factor of \(\frac{1}{2}\) and center (0, 0)
ΔGJH is dilated (enlarged) to ΔG’J’H’ and the angles are the same.
The coordinates of the vertices of ΔGJH have been changed after dilation.
a scale factor of \(\frac{1}{2}\) and center of dilation.

Check Understanding

Question 1.
Polygon BCDE has vertices B(5, 1), C(5, 6), D(10, 6), and E(10, 1). If B’C’D’E’ is a dilation of BCDE with scale factor 4 and center (0, 0), give the coordinates of B’C’D’E’.
Answer:
The scale factor in this dilation is 4.
Co-ordinates of B’C’D’E’.
B'(20, 4)
C'(20, 24)
D'(40, 24)
E'(40, 4))
Explanation:
Every coordinate of Polygon BCDE is multiplied by the scale factor of 4,
to obtain the enlarged Polygon B’C’D’E’.
In other words, if the scale factor is k,
the coordinates (x,y) are transformed to (kx,ky).
Polygon BCDE has vertices B(5, 1), C(5, 6), D(10, 6), and E(10, 1).
B’C’D’E’ is a dilation of BCDE with scale factor 4 are,
B'(20, 4)
C'(20, 24)
D'(40, 24)
E'(40, 4)

Question 2.
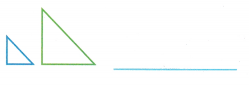
Does the pair of figures show a dilation with scale factor 4?
A.

Answer:
No
Explanation:
By comparing these two figures,
the scaling factor looks like 2.

B.

Answer:
Yes
Explanation:
By comparing these two figures,
the scaling factor looks like 4.

On Your Own

Question 3.
Reason Figure S’ is a dilation of Figure S.

A. Is the scale factor greater than 1 or less than 1? _______
Answer:
The scale factor is greater than 1.
Explanation:
By observing the above figure,
Figure S’ is a dilation of Figure S, and the scale factor is greater than 1.
Figure S’ is a dilation of Figure S and is enlargement.

B. Is Figure S congruent to Figure S’? _______
Answer:
No
Explanation:
Two geometric figures are said to be congruent, or to be in the relation of congruence,
if it is possible to superpose one of them on the other so that they coincide throughout.
Figure S is congruent to Figure S’ is not congruent due to S is smaller then S’.

C. Is the dilation a reduction? _______
Answer:
Yes
Explanation:
Dilation is the process of resizing or transforming an object.
It is a transformation that makes the objects smaller or larger with the help of the given scale factor.
The new figure obtained after dilation is called the image and the original image is called the pre-image.
Dilation can be of two types:

• Expansion – When the size of an object is increased.
• Contraction – When the size of an object is decreased.

Question 4.
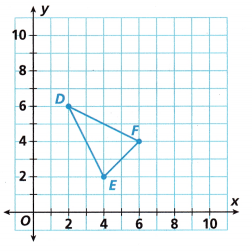
Use Tools Dilate ∆DEF with scale factor \(\frac{3}{2}\) and center (0, 0).

A. Find the coordinates of vertices D, E, and F.
__________________________
Answer:

Answer:
D(2, 6)
E(4, 2)
F(6, 4)
Explanation:
When a dilation in the coordinate plane has the origin as the center of dilation,
Find the points on the dilated image by multiplying the x- and y-coordinates of the original figure.
For scale factor k, the algebraic representation of the dilation is (x, y) → (kx, ky).
k = \(\frac{3}{2}\)
(x, y) → (\(\frac{3}{2}\)x, \(\frac{3}{2}\)y)
D(2, 6)  → D'(2 x 3/2, 6 x 3/2) = D'(3, 9)
E(4, 2)  → E'(4 x 3/2, 2 x 3/2) = E'(6, 3)
F(6, 4)  → F'(6 x 3/2, 4 x 3/2) = F'(9, 6)

B. Multiply each coordinate of each vertex by the scale factor to find the coordinates of vertices D’, E’ and F’.
Answer:
D(2, 6)  → D'(2 x 3/2, 6 x 3/2) = D'(3, 9)
E(4, 2)  → E'(4 x 3/2, 2 x 3/2) = E'(6, 3)
F(6, 4)  → F'(6 x 3/2, 4 x 3/2) = F'(9, 6)
Explanation:
When a dilation in the coordinate plane has the origin as the center of dilation,
Find the points on the dilated image by multiplying the x- and y-coordinates of the original figure.
For scale factor k, the algebraic representation of the dilation is (x, y) → (kx, ky).
k = \(\frac{3}{2}\)
(x, y) → (\(\frac{3}{2}\)x, \(\frac{3}{2}\)y)
D(2, 6)  → D'(2 x 3/2, 6 x 3/2) = D'(3, 9)
E(4, 2)  → E'(4 x 3/2, 2 x 3/2) = E'(6, 3)
F(6, 4)  → F'(6 x 3/2, 4 x 3/2) = F'(9, 6)

C. Graph and label the vertices D’, E’, and F’. Draw rays to connect each corresponding vertex with the center of dilation.
Answer:

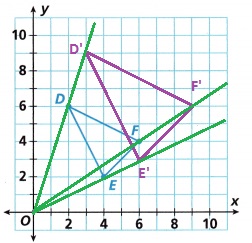
Explanation:
Vertices in graph are the points where two or more line segments or edges meet.

D. Represent the dilation algebraically.
___________________
Answer:
(x, y) → (\(\frac{3}{2}\)x, \(\frac{3}{2}\)y)
Explanation:
When a dilation in the coordinate plane has the origin as the center of dilation,
we can find points on the dilated image by multiplying the x- and y-coordinates of the original figure by the scale factor.
For scale factor k, the algebraic representation of the dilation is (x, y) → (kx, ky).
So, algebraic expression is (x, y) → (\(\frac{3}{2}\)x, \(\frac{3}{2}\)y).

Question 5.
Figure J’K’L’M’ is a dilation of Figure JKLM. The center of dilation is the origin, (0, 0).

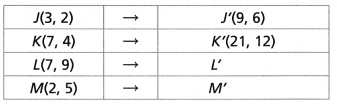
A. Given the coordinates of J, J’, K, and K’, what is the scale factor of the dilation?
___________________
Answer:
Scale factor of Dilation is 3.
Explanation:
Scale Factor is defined as the ratio of the size of the new image to the size of the old image.
The center of dilation is a fixed point in the plane.
Based on the scale factor and the center of dilation,
the dilation transformation is defined.
If the scale factor is more than 1, then the image stretches.

B. Use the scale factor to complete the table for points L’ and M’.
Answer:

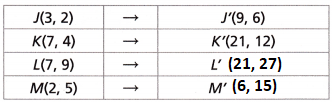
Explanation:
The scale factor is a measure for similar figures,
who look the same but have different scales or measures.
Scale factor used in the above table is 3.
The scale factor states the scale by which a figure is bigger or smaller than the original figure.

C. Represent the dilation algebraically.
Answer:
k = 3
(x, y) → (kx, ky)
(x, y) → (3x, 3y)
Explanation:
When a dilation in the coordinate plane has the origin as the center of dilation,
Find the points on the dilated image by multiplying the x- and y-coordinates of the original figure.
For scale factor k, the algebraic representation of the dilation is (x, y) → (kx, ky).
k = 3
(x, y) → (kx, ky)
(x, y) → (3x, 3y)

Question 6.
Graph ∆TUV with vertices T(4, 2), U(2, 0), and V(2, 4). Dilate the figure by a scale factor of \(\frac{5}{2}\) with a center of dilation of (0, 0). Graph ∆T’U’V’.

Answer:

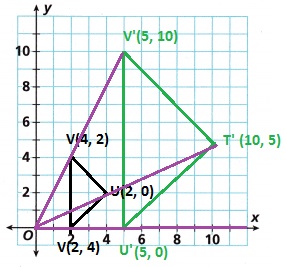
Explanation:
When a dilation in the coordinate plane has the origin as the center of dilation,
Find the points on the dilated image by multiplying the x- and y-coordinates of the original figure.
For scale factor k, the algebraic representation of the dilation is (x, y) → (kx, ky).
k = \(\frac{5}{2}\)
(x, y) → (\(\frac{5}{2}\)x, \(\frac{5}{2}\)y)
T(4, 2)  → T'(4 x 5/2, 2 x 5/2) = T'(10, 5)
U(2, 0)  → U'(2 x 5/2, 0 x 5/2) = U'(5, 0)
V(2, 4)  → V'(2 x 5/2, 4 x 5/2) = V'(5, 10)

Question 7.
STEM An ophthalmologist is a doctor who studies the eye. The ophthalmologist records the effect of changes in lighting on the size of the pupil of an eye and graphs the results on a coordinate plane.

A. What is the scale factor of the dilation from P to P’? _________
Answer:
The scale factor is \(\frac{2}{3}\).
Explanation:
We see that the circle has decreased in its size.
Therefore, the scale factor is =  Dimension of the new shape ÷ Dimension of the original shape
= Radius of the smaller circle ÷  Radius of the  larger circle
= 2  ÷ 3
A scale factor of \(\frac{2}{3}\) and center of dilation
Therefore, the scale factor is \(\frac{2}{3}\)

B. Graph a dilation of P using scale factor \(\frac{1}{3}\).
Answer:
Green color circle below the graph is graph with a dilation of P using scale factor \(\frac{1}{3}\).

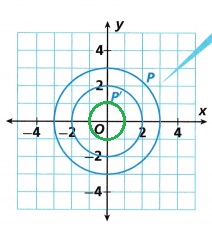
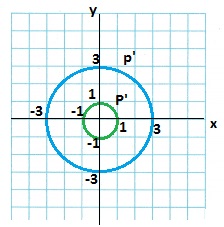
Explanation:
The scale factor can either increase the size of an object or decrease the size of an object.
The basic formula to find the scale factor of a dilated figure is:
Scale factor = Dimension of the new shape ÷ Dimension of the original shape.
We see that the circle has decreased in its size.
Therefore, the scale factor is =  Dimension of the new shape ÷ Dimension of the original shape
= Radius of the smaller circle ÷  Radius of the  larger circle
= 1  ÷ 3
A scale factor of \(\frac{1}{3}\) and center of dilation
Therefore, the scale factor is \(\frac{1}{3}\)

I’m in a Learning Mindset!

Did I have confidence in my answer? What specific evidence do I have that I found a scale factor of a dilation correctly?
Answer:
Yes,
Explanation:
Scale Factor is defined as the ratio of the size of the new image to the size of the old image.
The center of dilation is a fixed point in the plane.
Based on the scale factor and the center of dilation, the dilation transformation is defined.

Lesson 2.2 More Practice/Homework

Question 1.
Reason Which shape shows a dilation of Figure V? Justify your reasoning.

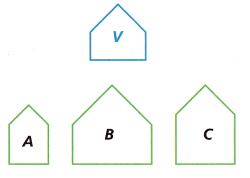
Answer:
Figure B,

Explanation:
The scale factor of a dilation is the ratio of the side lengths of the image to the preimage.
Point of intersection of lines through each pair of corresponding vertices in a dilation is called center of dilation.
The center of dilation is a fixed point in the plane.
Based on the scale factor and the center of dilation, the dilation transformation is defined.

Question 2.
Use Tools What is the scale factor of the dilation from the smaller square to the larger?

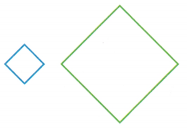
Answer:
A scale factor of \(\frac{4}{1}\) and center of dilation
Therefore, the scale factor is \(\frac{4}{1}\)
Explanation:
Dilation is the process of resizing or transforming an object.
It is a transformation that makes the objects smaller or larger with the help of the given scale factor.
The new figure obtained after dilation is called the image and the original image is called the pre-image.
We see that the square has increased in its size.
Therefore, the scale factor is =  Dimension of the new shape ÷ Dimension of the original shape
= Area of the smaller square ÷  Radius of the  larger circle
= 4 ÷ 1
A scale factor of \(\frac{4}{1}\) and center of dilation,
Therefore, the scale factor is \(\frac{4}{1}\).

Question 3.
Identify the center of dilation for the given figures.

___________________
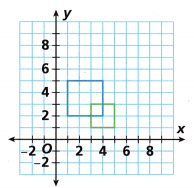
Answer:
C(7, -1)
Explanation:
Dilation geometry has an important concept referred to as the ‘center of dilation’.
Dilation transforms the size of the figure which may either increase or decrease.
The resizing happens from a point called the center of dilation.
It is the center of dilation from which the objects/figures are expanded or contracted.
In the figure shown below, the square is enlarged from the center of dilation which is marked as ‘C’.

Question 4.
Polygon WXYZ has vertices W(4, 2), X(6, 4), Y(2, 3), and Z(4, 5). If W’X’Y’Z’ is a dilation of WXYZ with center of dilation (0, 0) and vertex coordinates W'(2, 1), X'(3, 2), Y'(1, 1.5), and Z'(2, 2.5), find the scale factor.
Answer:
The scale factor in this dilation is 1/2.
Explanation:
Every coordinate of Polygon WXYZ is multiplied by the scale factor of 1/2,
to obtain the reduced Polygon W’X’Y’Z’.
In other words, if the scale factor is k,
the coordinates (x,y) are transformed to (kx,ky).
W(4, 2)= W'(2, 1)
X(6, 4)= X'(3, 2)
Y(2, 3)= Y'(1, 1.5)
Z(4, 5)= Z'(2, 2.5)

Test Prep

Question 5.
Dilate ABCD with a scale factor of 2 and center (0, 0).

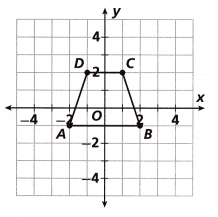
Answer:

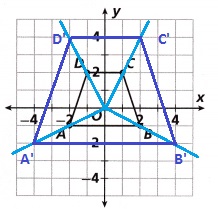
The scale factor in this dilation is 2.
Explanation:
Every coordinate of Polygon ABCD is multiplied by the scale factor of 2,
to obtain the reduced Polygon A’B’C’D’.
In other words, if the scale factor is k =2,
the coordinates (x,y) are transformed to (kx,ky).
(x, y) → (kx, ky)
(x, y) → (2x, 2y)
(x, y)→ (2x, 2y)
A(-2, -1) →  A'(-4, -2)
B(2, 1) → B'(4, 2)
C(1, 2) → C'(2, 4)
D(1, 2) → D'(2, 4)

Question 6.
∆MNP has vertices M( 4, 8), N(12, 6), and P(2, 4). ∆M’N’P’ is a dilation of ∆MNP with a scale factor of \(\frac{1}{2}\) and center (0, 0). Select the coordinates of the vertices of ∆M’N’P’.
A. M'( 1, 2), N'(2, 1), and P'( 1, 2)
B. M'(2, 4), N'(6, 3), and P'(1, 2)
C. M'(4, 8), N'(12, 6), and P'(2, 4)
D. M'(8, 16), N'(24, 12), and P'(4, 8)
Answer:
B. M'(2, 4), N(6, 3), and P'(1, 2)
Explanation:
∆MNP has vertices M( 4, 8), N(12, 6), and P(2, 4). ∆M’N’P’ is a dilation of ∆MNP with a scale factor of \(\frac{1}{2}\) and center (0, 0).
k = 2
(x, y) → (kx, ky)
(x, y) → (x/2, y/2)
M( 4, 8)  →  M'(2, 4),
N(12, 6)  →  N'(6, 3)
P(2, 4) →  P'(1, 2)

Question 7.
A triangle has angles of 30°, 60°, and 90°. It is dilated by a scale factor of 3. Give the angle measures of the dilation of the triangle.
Answer:
Dilated by a scale factor of 3

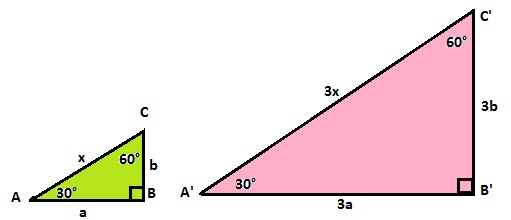
Explanation:
There will be no change in the angles of the triangle as the properties of triangle says,
the sum of the internal angles of the triangle is 180°.
There will be change in the lengths of sides of the triangle, but not the angles of the triangle.

Spiral Review

Question 8.
Translate the shape 3 units up and 2 units left.

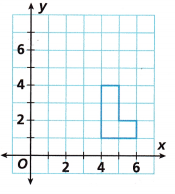
Answer:

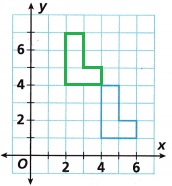
Explanation:
The shape 3 units up and 2 units left translated or shifted.
green color shape is the resultant shapes after shifting 3 units up and 2 units left.

Question 9.
What single transformation is represented by the rule P(x, y) → P’(-x, -y)?
___________________
Answer:
180 Degree Rotation is represented by the rule P(x, y) → P’(-x, -y).
Explanation:
When rotating a point 180 degrees counterclockwise about the origin,
our point P(x,y) becomes P'(-x,-y).
So all we do is make both x and y as negative.