We included HMH Into Math Grade 8 Answer Key PDF Module 2 Lesson 1 Investigate Reductions and Enlargements to make students experts in learning maths.
HMH Into Math Grade 8 Module 2 Lesson 1 Answer Key Investigate Reductions and Enlargements
I Can identify and perform enlargements and reductions.
Spark Your Learning
Rachel wants to enlarge her company logo for a sign. Sketch an enlargement of the Roofs by Rachel logo. Use your protractor to make sure the angle measurements of your enlargement stay the same as the original.
How are the two images alike? How are they different? Describe your findings.


Answer

Explanation:
Enlargement scale factor (ESF) = \(\frac{Big}{Small}\)
let K is the enlargement factor
K = \(\frac{Big}{Small}\)
Big = K x small
The size of the Rachel company logo after an enlargement of the Roofs by Rachel logo is same as the original.
Turn and Talk Write ratios comparing the lengths of the short and long sides of the original parallelogram and also of your enlarged parallelogram. What do you find?
Answer:
Ratios comparing the lengths of the short and long sides of the original parallelogram are of 1 : K.
Explanation:
Enlargement scale factor (ESF) = \(\frac{Big}{Small}\)
let K is the enlargement factor,
K = \(\frac{Big}{Small}\)
Big = K x small
The size of the the lengths of the short and long sides of the original parallelogram are of 1 : K ratio.
Build Understanding
Many computers and phones use reductions, called thumbnails, to represent images. Reductions are transformations that keep the proportions of the original image but are smaller in size.

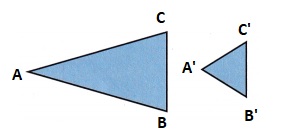
1. A. Triangle ABC is a drawing of the side of a roof. Use a ruler and a protractor to measure ∆ABC.
∠A measures ____ °
∠B measures ____ °
∠C measures ____ °
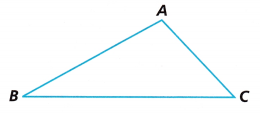
\(\overline{A B}\) measures _____ inch(es).
\(\overline{B C}\) measures _____ inch(es).
\(\overline{A C}\) measures _____ inch(es).
Answer:
∠A measures 100°
∠B measures 30°
∠C measures 50°
\(\overline{A B}\) measures 3 inch(es).
\(\overline{B C}\) measures 4 inch(es).
\(\overline{A C}\) measures 2 inch(es).
Explanation:
By using protractor all the angles are measured, recorded measurements are as shown in the above.
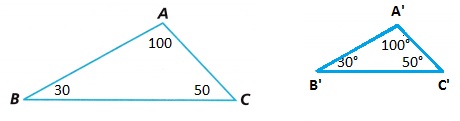
B. If ∆A’B’C’ is a reduction of ∆ABC that results in ∆A’B’C’ having a perimeter exactly half that of ∆ABC, what are the measurements of ∆A’B’C’?
∠A’ measures ____° \(\overline{A^{\prime} B^{\prime}}\) measures ____ inches
∠B’ measures ____° \(\overline{B^{\prime} C^{\prime}}\) measures ____ inches
∠C’ measures ____° \(\overline{A^{\prime} C^{\prime}}\) measures ____ inches
Answer:
∠A’ measures 100° \(\overline{A^{\prime} B^{\prime}}\) measures 1.5 inches.
∠B’ measures 30° \(\overline{B^{\prime} C^{\prime}}\) measures 2 inches.
∠C’ measures 50° \(\overline{A^{\prime} C^{\prime}}\) measures 1 inches.
Explanation:
∆A’B’C’ having a perimeter exactly half that of ∆ABC
every side of the triangle is reduced to half, then the perimeter is also will be half
∆ABC’ perimeter is
AB + BC + AC = 3 + 4 + 2 = 9 inches
∆A’B’C’ having a perimeter is
A’B’ + B’C’ + A’C’ = 1.5 + 2 + 1 = 4.5 inches
4.5 exactly half that of ∆ABC
Reduction scale factor (RSF) = \(\frac{small}{big}\)
half = \(\frac{small}{big}\)
\(\frac{1}{2}\) = \(\frac{A’B’}{AB}\)
\(\frac{1}{2}\) = \(\frac{B’C’}{BC}\)
\(\frac{1}{2}\) = \(\frac{A’C’}{AC}\)
fine the new image triangle values
\(\frac{1}{2}\) = \(\frac{A’B’}{3}\)
A’B’ = \(\frac{1 X 3}{2}\) = 1.5 inches
\(\frac{1}{2}\) = \(\frac{B’C’}{4}\)
B’C’ = \(\frac{1 X 4}{2}\) = 2 inches
\(\frac{1}{2}\) = \(\frac{A’C’}{2}\)
A’C’ = \(\frac{1 X 2}{2}\) = 1 inch
∠A’ measures 100° \(\overline{A^{\prime} B^{\prime}}\) measures 1.5 inches
∠B’ measures 30° \(\overline{B^{\prime} C^{\prime}}\) measures 2 inches
∠C’ measures 50° \(\overline{A^{\prime} C^{\prime}}\) measures 1 inches
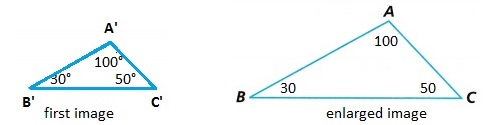
C. Draw ∆A’B’C’ as a reduction. Find the new image triangle values?
Answer:
Explanation:
\(\frac{1}{2}\) = \(\frac{A’B’}{3}\)
A’B’ = \(\frac{1 X 3}{2}\) = 1.5 inches
\(\frac{1}{2}\) = \(\frac{B’C’}{4}\)
B’C’ = \(\frac{1 X 4}{2}\) = 2 inches
\(\frac{1}{2}\) = \(\frac{A’C’}{2}\)
A’C’ = \(\frac{1 X 2}{2}\) = 1 inch
∠A’ measures 100°, \(\overline{A^{\prime} B^{\prime}}\) measures 1.5 inches
∠B’ measures 30°, \(\overline{B^{\prime} C^{\prime}}\) measures 2 inches
∠C’ measures 50°, \(\overline{A^{\prime} C^{\prime}}\) measures 1 inches
D. Explain how you know it is a reduction.
Answer:
When Scale Factor is between 0 and 1, the new shape is a reduction (smaller).
Or less than 100%. When Scale Factor is above 1, new shape is an enlargement (bigger).
The size of an enlargement/reduction is described by its scale factor.
Explanation:
Reduction scale factor (RSF) = \(\frac{small}{big}\)
half = \(\frac{1}{2}\) = \(\frac{small}{big}\)
\(\frac{1}{2}\) = \(\frac{A’B’}{AB}\)
\(\frac{1}{2}\) = \(\frac{B’C’}{BC}\)
\(\frac{1}{2}\) = \(\frac{A’C’}{AC}\)
Turn and Talk What would happen if you enlarged ∆A’B’C’? Could you make a new image that is congruent to the original figure ∆ABC? If so, how?
Answer:
Yes,
Explanation:
The enlarged ∆A’B’C’, a new image that is congruent to the original figure ∆ABC.
if the enlargement factor is twice or 2, then original i mage will be formed.
Enlargement scale factor (ESF) = \(\frac{big}{small}\)
2 = \(\frac{big}{small}\)
big = 2 x small
Look at this photo. As the train tracks get closer to the front, they appear larger. A coordinate grid can help show how the tracks’ apparent size changes.

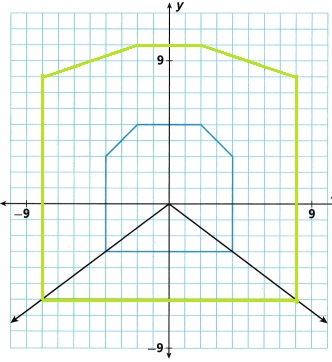
2. Samuel wants to draw a railroad tunnel on a grid. First he draws the far end of the tunnel in blue as shown, then he decides to use rays to help him accurately enlarge the image.
A. Samuel draws two rays. Each starts at the origin and passes through a vertex of the blue preimage. He uses the rays to help sketch the floor of the tunnel closest to the viewer.
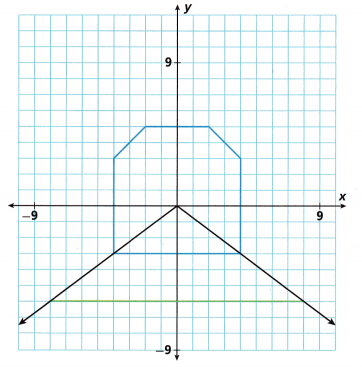
How do the rays help him draw the floor of the tunnel closest to the viewer?
Answer:
Two rays helps to enlarge the floor of the tunnel closest to the viewer.
Explanation:
From the center the rays are extended to all vertices,
the original figure scale factor is multiplied by 2.
The resultant figure is double the original picture.
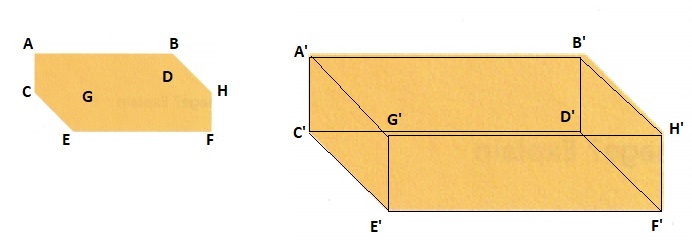
B. Draw additional rays from the origin through the vertices of Samuel’s preimage. Use those rays to complete the enlarged image.
Answer:
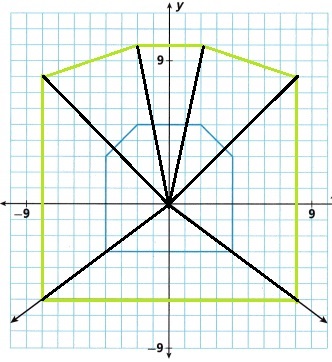
Explanation:
From the center the rays are extended to all vertices,
the original figure scale factor is multiplied by 2.
The resultant figure is double the original picture.
C. Look at your new image. Is it the same shape as the preimage? Explain how you know.
______________________
______________________
Answer:
Yes,
Explanation:
A transformation is a change in the position, size, or shape of a new geometric figure.
The preimage of a transformation is the shape before the transformation
The new figure is called the image and original figure is known as preimage.
First image rays which are drawn are extended and points marked on the chart as shown in the above figure.
3. You can make reductions on a coordinate grid.
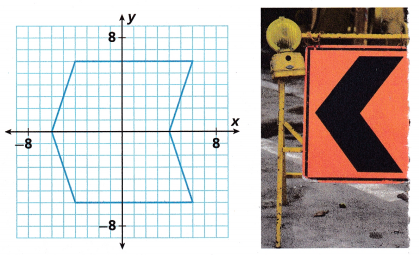
A. Draw rays from the origin through the vertices of the given shape. How can these rays help you reduce the shape?
______________________
______________________
Answer:
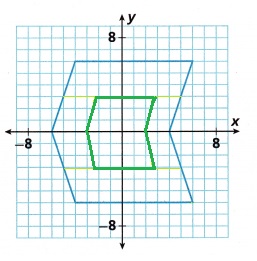
Explanation:
When Scale Factor is between 0 and 1, the new shape is a reduction (smaller).
Or less than 100%. When Scale Factor is above 1, new shape is an enlargement (bigger).
The size of an enlargement/reduction is described by its scale factor.
Original image or figure is reduced to half by extending the rays as shown in the above figure.
B. Reduce the shape so the sides are half the original lengths. Use the grid to sketch your new image.
Answer:
Yes,
Explanation:
The grid method is an effective way to transfer or enlarge the original image onto canvas,
ensuring correct proportions.
C. How can you be sure your image shows an accurate reduction?
______________________
Answer:
By comparing the original image blue colored sketched to the green colored image.
Explanation:
Reduction is a transformation of an object that has the same shape,
but decreases in size of the object.
Reduction of a shape can be done by a scale factor of 2.
Check Understanding
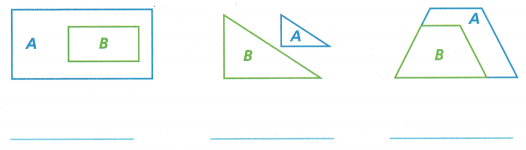
Question 1.
Does this pair show a reduction? Why or why not?

Answer:
No,
Explanation:
Reduction ration of the sides of the triangles are not in proper ratio.
Reduction is a transformation of an object that has the same shape,
but decreases in size of the object.
Question 2.
Sketch an enlargement of the shape in the given space. Explain how you know it’s an enlargement.

Answer:
Explanation:
Reduction is a transformation of an object that has the same shape,
but decreases in size of the object.
Big shape is enlarged figure of small cuboid shape.
Enlargement scaling factor is 2,
length of A’B’ is 2AB,
all lengths of every side is multiplied by 2.
On Your Own
Question 3.
Identify whether the transformation from each blue Figure A to green Figure B is an enlargement or a reduction.
Answer:
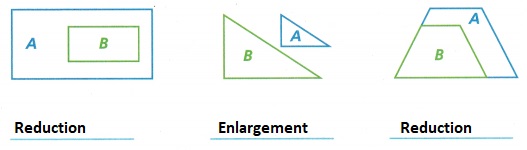
Explanation:
Reduction ration of the sides of the triangles are not in proper ratio.
Reduction is a transformation of an object that has the same shape,
but decreases in size of the object.
An enlargement is a type of transformation where we change the size of the original shape,
to make it bigger or smaller by multiplying it by a scale factor.
Question 4.
Use the coordinate plane to sketch an enlargement with side lengths twice those in the figure shown.
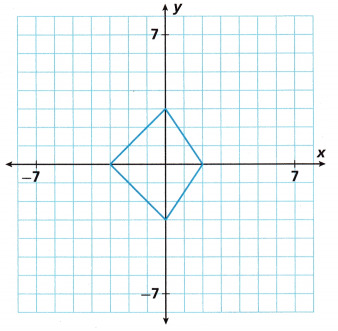
Answer:
Figure ABCD is enlarged with side lengths twice those in the figure shown A’B’C’D’
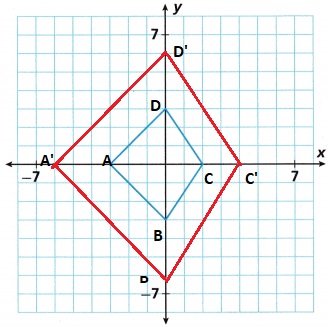
Explanation:
An enlargement is a type of transformation where we change the size of the original shape,
to make it bigger or smaller by multiplying it by a scale factor.
To use a center of enlargement we need to draw lines from the center of enlargement,
through the vertices of the original shape.
Question 5.
Reason Fredrick drew a reduction of a phone. Is the reduction accurate? Why or why not?
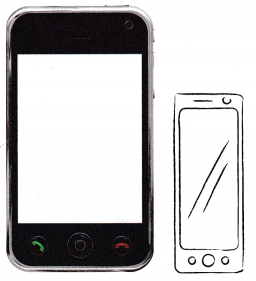
Answer:
No, the ratio of reduction is not correct.
Explanation:
Reduction ration of the sides of the triangles are not in proper ratio.
Reduction is a transformation of an object that has the same shape,
but decreases in size of the object.
Reduction of a shape can be done by a scale factor of 2.
Question 6.
Use Tools Draw a reduction of the figure with dimensions half those of the original figure.

Answer:
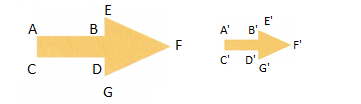
Explanation:
Reduction scale factor (RSF) = \(\frac{small}{big}\)
half = \(\frac{1}{2}\) = \(\frac{small}{big}\)
\(\frac{1}{2}\) = \(\frac{A’B’}{AB}\)
\(\frac{1}{2}\) = \(\frac{B’C’}{BC}\)
\(\frac{1}{2}\) = \(\frac{C’D’}{CD}\)
\(\frac{1}{2}\) = \(\frac{D’E’}{DE}\)
\(\frac{1}{2}\) = \(\frac{E’F’}{EF}\)
by new length of A’B’, B’C’, C’D’, D’E and E’F will form a new image as shown in the above figure.
Question 7.
Use Tools Use the coordinate plane to reduce the side lengths of the figure shown by half.
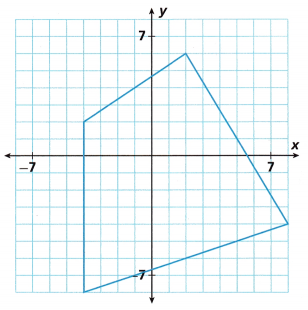
Answer:
Green color figure A’B’C’D’ is new figure is reduced to half of the original figure ABCD.
Explanation:
Reduction ration of the sides of the triangles are not in proper ratio.
Reduction is a transformation of an object that has the same shape,
but decreases in size of the object.
Reduction of a shape can be done by a scale factor of 2.
Question 8.
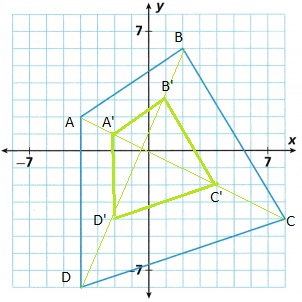
For each figure, determine if it is a reduction of Figure S.
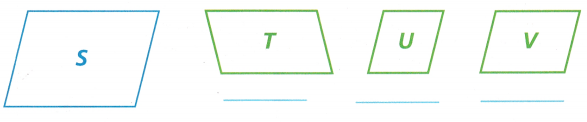
Answer:
Figure V is a reduction of Figure S
Explanation:
Reduction ration of the sides of the triangles are not in proper ratio.
Reduction is a transformation of an object that has the same shape,
but decreases in size of the object.
Reduction of a shape can be done by a scale factor of 2.
I’m in a Learning Mindset!
How does my mindset affect my confidence with reducing and enlarging figures?
_______________________
_______________________
Answer:
Answer may vary,
Explanation:
when we start on reducing and enlarging figures,
our mindset affect the confidence on enlarging.
Lesson 2.1 More Practice/Homework
Question 1.
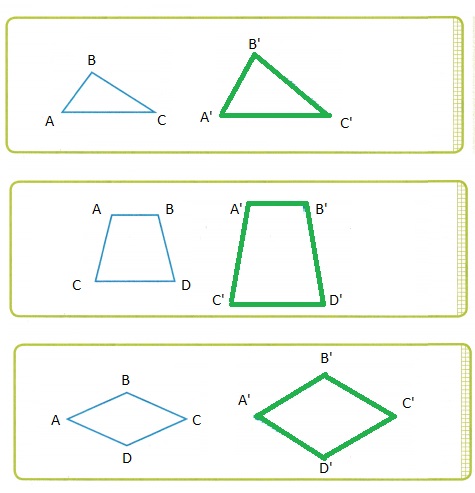
Use Tools In the space provided, sketch an enlargement that has sides \(\frac{3}{2}\) the length of each given figure.
Answer:
Explanation:
Enlargement scale factor (ESF) = \(\frac{Big}{Small}\)
\(\frac{3}{2}\) = \(\frac{Big}{Small}\)
Big = \(\frac{3 x small}{2}\)
The enlarged ∆A’B’C’, a new image that is congruent to the original figure ∆ABC.
if the enlargement factor is twice or 2, then original i mage will be formed.
Enlargement scale factor (ESF) = \(\frac{big}{small}\)
Big = \(\frac {3 x small}{2}\)
Big = 1.5 x small
Every side of original image is multiplied by 1.5
Question 2.
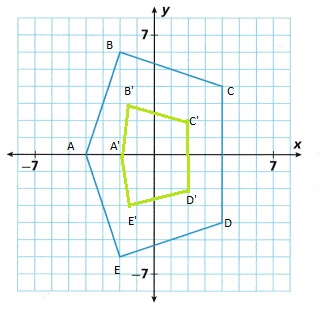
A. Use the coordinate plane to sketch a reduction of the irregular pentagon on the grid by any amount.
_________________________
Answer:
Explanation:
In the cartesian plane is defined as a two-dimensional coordinate plane,
which is formed by the intersection of the x-axis and y-axis.
The x-axis and y-axis intersect perpendicular to each other at the point called the origin.
Reduction is a transformation of an object that has the same shape,
but decreases in size of the object.
Reduction of a shape can be done by a scale factor of 2.
B. Measure the angles of both figures with a protractor. Explain your findings.
______________________
Answer:
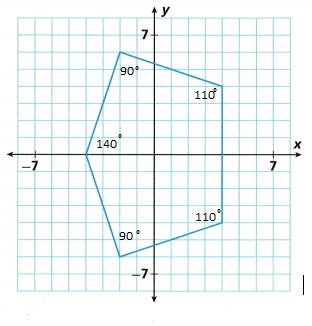
Explanation:
By placing protractor on the figure, the angles are measured and recorded.
Question 3.
A certain Figure Q is enlarged to form Figure P. Are Figures Q and P congruent? Why or why not?
Answer:
YES,
Explanation:
In geometry, two figures or objects are congruent if they have the same shape and size,
or if one has the same shape and size as the mirror image of the other.
If a Figure Q is enlarged to form Figure P.
Figure P and Q are congruent due to the angles are equal.
Figure P and Q sides may be differ by its lengths.
Test Prep
Question 4.
In which of the following has Figure 1 been enlarged to form Figure 2?
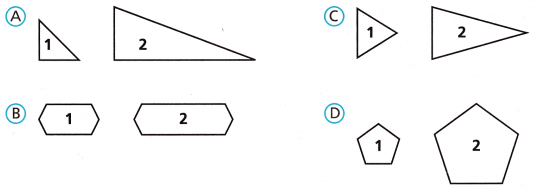
Answer:
Option (2)
Explanation:
An enlargement is a type of transformation where we change the size of the original shape,
to make it bigger or smaller by multiplying it by a scale factor.
To use a center of enlargement we need to draw lines from the center of enlargement,
through the vertices of the original shape.
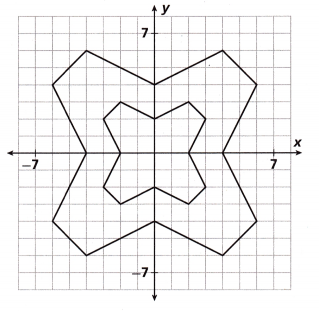
Question 5.
One of the shapes on the coordinate grid was transformed into the other shape. Which term could describe the transformation?
A. reflection
B. enlargement
C. translation
D. rotation
Answer:
Rotation:
Explanation:
Rotating of an object means turning it around a point, which is called the center of rotation.
In the above shape on the coordinate grid was transformed by rotating from the origin.
Either 90 clockwise or counter clockwise direction.
clockwise or counter clockwise direction.
The resultant figure is as same as the original figure as shown in the above figure.
Spiral Review
Question 6.
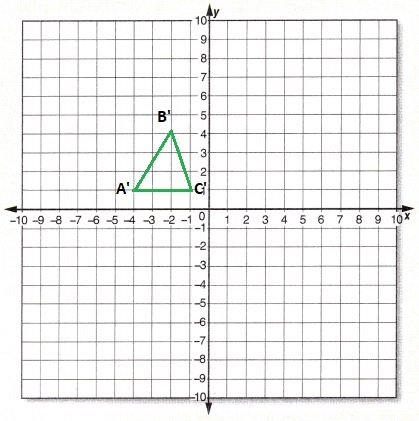
Rotate ∆ABC 90° counterclockwise about the origin.
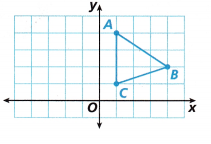
Answer:
90 Degree counter clockwise rotation.
Explanation:
When rotating a point 90 degrees counterclockwise about the origin our point A(x,y) becomes A'(-y,x).
In other words, switch x and y and make y negative
A(1, 4) —> A'(-4, 1)
B(4, 2) —> B'(-2, 4)
C(1, 1) —> C'(-1, 1)
The above new co ordinates form a per image as shown in the above fugure.
Question 7.
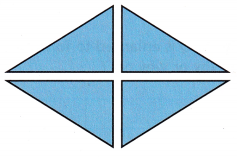
This design is made using only one type of transformation multiple times. Which one type of transformation is this?
Answer:
Reflection
Explanation:
Consider cutting out a pre image, lifting it, and repositioning it face down.
That’s called a reflection or a flip.
A reflection image is a reflection of the pre image.