Into Math Grade 8 Module 2 Answer Key Transformations and Similarity

We included HMH Into Math Grade 8 Answer Key PDF Module 2 Transformations and Similarity to make students experts in learning maths.

HMH Into Math Grade 8 Module 2 Answer Key Transformations and Similarity

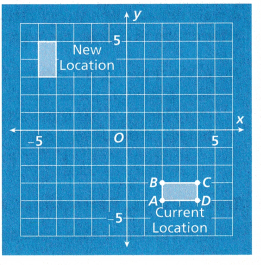
Do You Haul Bones?

A museum received a crate containing a set of dinosaur bones. You need to move the crate from its current location to the location marked on the grid. Each unit on the grid represents 1 meter.
How could you use a sequence of transformations to haul the crate to its new location?

Turn and Talk
Why might the museum not want you to use a reflection to move the crate?

Are You Ready?

Complete these problems to review prior concepts and skills you will need for this module.

Polygons in the Coordinate Plane

Determine the length, in units, of each side of the figure on the coordinate plane.

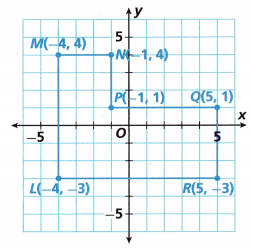
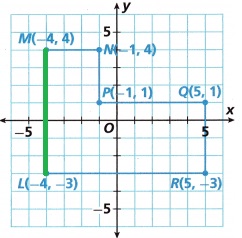
Question 1.
\(\overline{L M}\) ________
Answer:
7 units,
Explanation:

The distance between the points (x1, y1) and (x2, y2) is given by the formula,
SQRT (x2 – x1)² + (y2 – y1)²
L(-4, -3), M(-4, 4)
SQRT (-4 – (-4))²  + (4 – (-3))²
SQRT (-4 + 4)²  + (4 + 3)²
SQRT (0)²  + (7)²
\(\sqrt{0 + 49}\)
\(\sqrt{49}\) = 7 units.

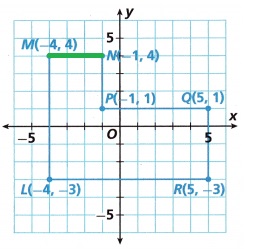
Question 2.
\(\overline{M N}\) ________
Answer:
3 units,
Explanation:

The distance between the points (x1, y1) and (x2, y2) is given by the formula,
SQRT (x2 – x1)² + (y2 – y1)²
N(-1, 4), P(-1, 1)
SQRT{(-1 – (-1))²  + (1 – 4))²}
SQRT {0 + (-1 + 4)²}
SQRT {(3)²}
\(\sqrt{9}\) = 3 units.

Question 3.
\(\overline{N P}\) ________
Answer:
3 units,
Explanation:

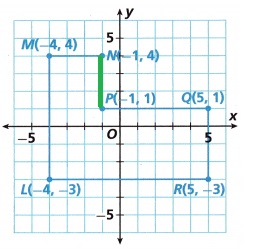
The distance between the points (x1, y1) and (x2, y2) is given by the formula,
SQRT (x2 – x1)² + (y2 – y1)²
N(-1, 4), P(-1, 1)
SQRT{(-1 – (-1))²  + (1 – 4))²}
SQRT {0 + 3² }
SQRT {(3)²}
\(\sqrt{9}\) = 3 units.

Question 4.
\(\overline{P Q}\) ________
Answer:
6 units,
Explanation:

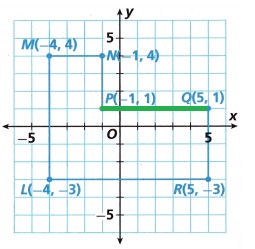
The distance between the points (x1, y1) and (x2, y2) is given by the formula,
SQRT (x2 – x1)² + (y2 – y1)²
P(-1, 1) , Q(5, 1),
SQRT{(5 – (-1))²  + (1 – 1))²}
SQRT {(5 + 1)²  + 0}
SQRT {(6)²  + (0)²}
\(\sqrt{36 + 0}\)
\(\sqrt{36}\) = 6 units.

Question 5.
\(\overline{Q R}\) ________
Answer:
4 units,
Explanation:

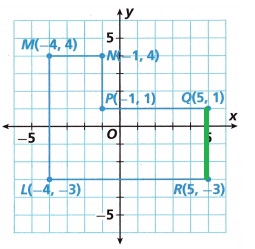
The distance between the points (x1, y1) and (x2, y2) is given by the formula,
SQRT (x2 – x1)² + (y2 – y1)²
Q(5, 1) , R(5, -3),
SQRT{(5 – 5)²  + (-3 – 1))²}
SQRT {(0)²  + (4)²}
\(\sqrt{0 + 16}\)
\(\sqrt{16}\) = 4 units.

Question 6.
\(\overline{P Q}\) ________
Answer:
6 units,
Explanation:

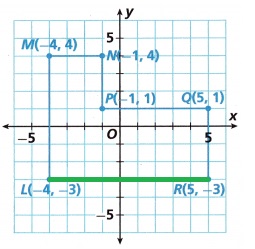
The distance between the points (x1, y1) and (x2, y2) is given by the formula,
SQRT (x2 – x1)² + (y2 – y1)²
R(5, -3) , S(-4, -3),
SQRT{((-4) – 5)²  + (-3 + 3))²}
SQRT {(-4 – 5)²  + 0}
SQRT {(-9)²  + (0)²}
\(\sqrt{81}\)
\(\sqrt{81}\) = 9 units.

Scale Drawings

A scale drawing of a school cafeteria has a scale of 1 inch : 4 feet. Use this information to answer each question.

Question 7.
In the drawing, the cafeteria dining room has a length of 18 inches. What is the actual length of the dining room?
Answer:
72 feet,
Explanation:

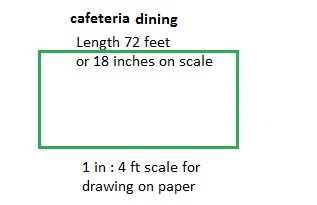
The cafeteria dining room has a length of 18 inches.
length = 18 inches
The actual length of the dining room,
18 x 4 = 72 feet

Question 8.
The actual width of the cafeteria kitchen is 42 feet. What is the width of the kitchen in the scale drawing?
Answer:
10.5 inches,
Explanation:

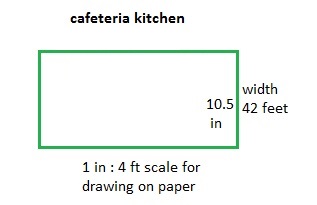
The actual width of the cafeteria kitchen is 42 feet,
the width of the kitchen in the scale drawing.
42/4 = 10.5 inches

Translations, Reflections, and Rotations

Draw the image of each transformation on the coordinate plane.

Question 9.
Rotate Triangle ABC 180° about the origin.

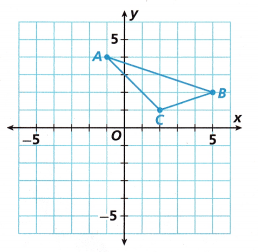
Answer:

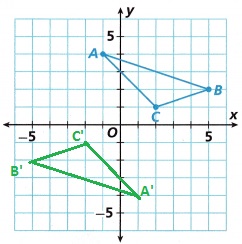
Explanation:
The rule for a rotation by 180° about the origin is (x, y)→(−x,−y)
A(-1, 4) → A'(1,−4)
B(5, 2) → B'(-5,−2)
C(2, 1) → C'(-2,−1)

Question 10.
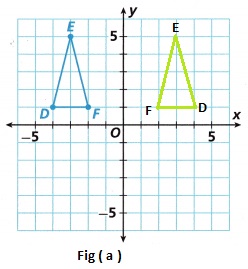
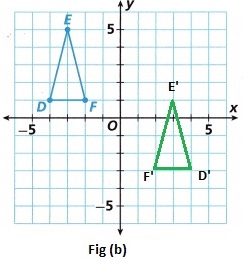
Reflect Triangle DEF across the y-axis, and then translate it 4 units down.

Answer:

Explanation:
In fig (a) the triangle is reflected to right side
The rule for a reflection over the y -axis is,
(x, y)→(−x, y)
D(-4, 1)→ D'(4, 1)
E(-3, 5)→ E'(3, 5)
F(-2, 1)→ F'(2, 1)
In fig (b) the triangle is shifted down to 4 units down.
subtract 4 from ‘y’ value, then
(x, y – 4)→(−x, y)
D'(4, 1 – 4) → D'(4, -3)
E'(3, 5 – 4) → E'(3, 1)
F'(2, 1 – 4) → F'(2, -3)