We included HMH Into Math Grade 8 Answer Key PDF Module 13 Volume to make students experts in learning maths.
HMH Into Math Grade 8 Module 13 Answer Key Volume
Reduce the Juice
A company wants to reduce the volume of its juice box by 20%. The diagram shows the dimensions of the company’s current juice box.

A. The new juice box’s volume will be ___________ cubic centimeters.
Answer:
The amount of space occupied by a three-dimensional object is called the object’s volume. The volume of a rectangular prism represents the amount of space it occupies. In other words, the volume of a rectangular prism is defined as the number of units utilised to fill it. A cubic unit is a unit of volume.
The volume of rectangle formula in maths is given by:
The volume of the Rectangle formula (V)= l × w × h.
Here,
l signifies the length of the rectangular prism
B represents the base of a rectangular prism
w is the width of a rectangular prism
volume = 10 x 6.5 x 4
volume= 260 cubic centimetres.
Therefore, the new juice box’s volume will be 260 cubic centimetres.
B. Produce two designs for new juice boxes with a reduced volume. Give the dimensions for each design.
Answer:
we need to design new juice boxes with a reduced volume.
The current juice box volume is 260 cubic centimetres.
Now the design 1 will be:
length: 9 cms
width: 5.5 cms
height: 3 cms
volume of design 1 box = 9 x 5.5 x 3 = 148.5 cubic centimetres
Now the design 2 will be:
length: 5 cms
width: 3 cms
height: 1 cms
volume of design 2 box = 5 x 3 x 1 = 15 cubic centimetres.
Turn and Talk
Question 1.
Explain how you determined the volume of a new juice box.
Answer:
The amount of space occupied by a three-dimensional object is called the object’s volume. The volume of a rectangular prism represents the amount of space it occupies. In other words, the volume of a rectangular prism is defined as the number of units utilised to fill it. A cubic unit is a unit of volume.
The volume of rectangle formula in maths is given by:
The volume of the Rectangle formula (V)= l × w × h.
according to the above formula, we can determine the volume of a new juice box.
Question 2.
Which of your designs for new juice boxes would require more materials to make? Explain your reasoning.
Answer:
According to the dimensions we require materials.
For example, in the above question, we take some dimensions for design 1 and design 2.
for design 1 box, we got a volume of 148.5 cubic centimetres and for design 2 we got 15 cubic centimetres.
I think design 1 needs more material to make because its volume is more than design 2.
Are You Ready?
Complete these problems to review prior concepts and skills you will need for this module.
The volume of Rectangular Prisms
For Problems 1-3, determine the volume of each rectangular prism.
Question 1.
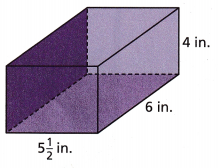
____________ in3
Answer:
given, length = 6 in,
width = 5 1/2 = 11/2 = 5.5 in,
height = 4 inches
By the volume of a rectangular prism formula, we have
Volume = l*w*h
volume = 6 x 5.5 x 4
volume = 132 cubic inches
Hence the volume of a rectangular prism is 132 cubic inches.
Question 2.
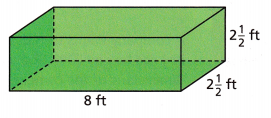
___________ ft3
Answer:
given, length = 8 ft
width = 2 1/2 = 5/2 = 2.5 ft
height = 2 1/2 = 5/2 = 2.5 ft
By the volume of a rectangular prism formula, we have
Volume = l*w*h
volume =8 x 2.5 x 2.5
volume = 50 cubic ft.
Hence the volume of a rectangular prism is 50 cubic ft.
Question 3.
a rectangular prism that is 7.3 centimeters by 8.5 centimeters by 4.2 centimeters ____________
Answer:
given, length = 8.5 cms (longest side)
width = 7.3 cms
height = 4.2 cms
By the volume of a rectangular prism formula, we have
Volume = l*w*h
volume =8.5 x 7.3 x 4.2
volume = 260.61 cubic centimetres.
Question 4.
A packing box is 3.5 feet by 1.4 feet by 1.8 feet. A box that is 3.1 feet by 1.1 feet by 1.4 feet is placed inside the first box. The rest of the box is filled with packing foam. How many cubic feet does the packing foam take up?
Answer:
given, length = 3.5 feet
width = 1.8 feet
height = 1.4 feet
By the volume of a rectangular prism formula, we have
Volume = l*w*h
volume = 3.5 x 1.8 x 1.4
volume of total box = 8.82 cubic feet
In that total box, the other box was placed. Now we find that box volume.
Volume of placed box = 3.1 x 1.4 x 1.1
volume = 4.774 cubic feet.
Now the rest of the box is filled with foam.
To get the volume of remaining we need to subtract.
the volume of the remaining place after placing the box = 8.82 – 4.774
remaining place = 4.046 cubic feet.
Therefore, 4.046 cubic feet does the packing foam take up.
Area of Circles
For Problems 5-7, determine the area of each circle. Use 3.14 for TV. Round each answer to the nearest hundredth.
Question 5.
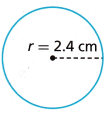
__________ cm2
Answer:
The area of a circle is the region covered or enclosed within its boundary. It is measured in square units.
Area of a Circle, A = πr2 square units.
we know the value of pi, π = 22/7 or 3.14 and r is the radius.
substitute the values in the formula:
given, radius = 2.4 cms
Area of a Circle = 22/7 x 2.4 x 2.4
Area of circle = 22/7 x 5.76
Area of circle = 18.0864
The nearest hundredth value is 19 square cms
Question 6.
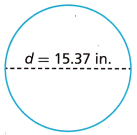
___________ in2
Answer:
The area of a circle is the region covered or enclosed within its boundary. It is measured in square units.
Area of a Circle, A = πr2 square units.
we know the value of pi, π = 22/7 or 3.14 and r is the radius.
substitute the values in the formula:
given, radius = 15.37 in
Area of a Circle = 22/7 x 15.37 x 15.37
Area of a circle = 22/7 x 236.2369
Area of a circle = 741.7838
The nearest hundredths value is 742 square inches.
Question 7.
a circle with a radius of 9.4 ft ____________
Answer:
The area of a circle is the region covered or enclosed within its boundary. It is measured in square units.
Area of a Circle, A = πr2 square units.
we know the value of pi, π = 22/7 or 3.14 and r is the radius.
substitute the values in the formula:
given, radius = 9.4 ft
Area of a Circle = 22/7 x 9.4 x 9.4
Area of a circle = 22/7 x 88.36
Area of a circle = 277.4504
The nearest hundredth value is 277 square ft.
Question 8.
On the ice of a hockey rink, there is one circle with a 12-inch diameter, and one with a 24-inch diameter. How much more area does the larger circle have than the smaller one? Explain how you know. Use 3.14 for π.
Answer:
Area of Circle = πr2 or πd2/4, square units
where π = 22/7 or 3.14
Area of small circle:
area = 3.14 x 12^2/4
area = 3.14×144/4
area = 452.16/4
area = 113.04
Area of large circle:
area = 3.14 x 24^2/4
area = 452.16
Now subtract and let the answer be x.
x = 452.16 – 113.04
x = 339.12 square units
Therefore, the larger circle is 339.12 square inches more than the smaller circle.