Into Math Grade 8 Module 11 Review Answer Key

We included HMH Into Math Grade 8 Answer Key PDF Module 11 Review to make students experts in learning maths.

HMH Into Math Grade 8 Module 11 Review Answer Key

Vocabulary

For Problems 1-3, choose the correct term from the Vocabulary box to complete each sentence.

Vocabulary
hypotenuse
leg
Pythagorean Theorem
Pythagorean triple

Question 1.
The ____________ describes the relationship leg among the lengths of the sides of any right triangle.
Answer:
Pythagorean Theorem,

Explanation:
The Pythagorean Theorem describes the relationship leg among the lengths of the sides of any right triangle.

Question 2.
A _____________ of a right triangle is one of the sides that forms the right angle.
Answer:
hypotenuse,

Explanation:
A hypotenuse of a right triangle is one of the sides that forms the right angle.

Question 3.
A _____________ is a set of three positive integers that could be the side lengths of a right triangle.
Answer:
Pythagorean triple,

Explanation:
A Pythagorean triple is a set of three positive integers that
could be the side lengths of a right triangle.

Question 4.
Write the converse of this statement: If a triangle has a right angle, then it is a right triangle.
Answer:
Converse: If a triangle is right triangle then it has a right angle,

Explanation:
Given to write the converse of this statement: If a triangle has a right angle, then it is a right triangle so it is Converse: If a triangle is right triangle then it has a right angle.

Concepts and Skills
Question 5.
Which set of side lengths could form a right triangle?
(A) 5 cm, 5 cm, and 10 cm
(B) 6 cm, 7 cm, and 8 cm
(C) 8 cm, 15 cm, and 17 cm
(D) 9 cm, 12 cm, and 16 cm
Answer:
(C) 8 cm, 15 cm, and 17 cm and
(D) 9 cm, 12 cm, and 16 cm,

Explanation:
To find which set of side lengths could form a right triangle is checking with bit(A) 5 cm, 5 cm, and 10 cm we have (5)² + (5)² = 10², 25 + 25 = 100, as 50 ≠ 100, checking with bit(B) 6 cm, 7 cm, and 8 cm we have (6)² + (7)² = 8², 36 + 49 = 64, as 85 ≠ 64,
checking with bit(C) 8 cm, 15 cm, and 17 cm we have
(8)² + (15)² = 17², 64 + 225 = 289, as 289 = 289,
now checking with bit(D) 9 cm, 12 cm, and 16 cm we have (9)² + (12)² = 16²,
81 + 144 = 225 as 225 =225, therefore bits (C) and (D) set of side lengths could form a right triangle.

Question 6.
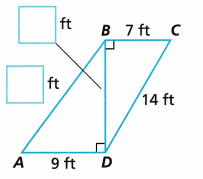
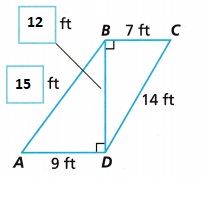
Use Tools The diagram represents a set of beams that form part of a bridge support. Label \(\overline{A B}\) and \(\overline{B D}\) with their lengths, rounded to the nearest foot. State what strategy and tool you will use to answer the question, explain your choice, and then find the answer.

Answer:

Explanation:
To find the distance of BD we calculate as BD² = (14)² – 7²,
BD² = 196 – 49 = 147, So BD is equal to square root of 147 = 12.12 nearly 12 ft, Now the distance of AB is AB² = (12)² + 9², AB² = 144 + 81 = 225, So AB is equal to square root of
225 = 15 ft, Used Tools the diagram represented a set of beams that form part of a bridge support.
Labelled \(\overline{A B}\) as 15 ft and\(\overline{B D}\) as 12 ft with their lengths and rounded to the nearest foot. Strategy used as both are right triangles is Pythagorean theorem.

For Problems 7 and 8, determine the unknown side length of each right triangle to the nearest hundredth.

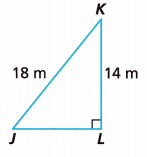
Question 7.
What is the length of \(\overline{J L}\)?

__________ meters
Answer:
The length of \(\overline{J L}\) is 11 meters,

Explanation:
Given side length of triangle KJL as KL 14 m and KJ as 18 m as triangle is right triangle applying
Pythagorean theorem to find the length of JL as JL² = (18)² – 14²,
JL² = 324 -196 = 128, So JL is equal to square root of 128 = 11.31 nearly 11 meters.

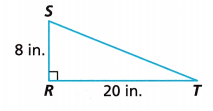
Question 8.
What is the length of \(\overline{S T}\)?

___________ inches
Answer:
The length of \(\overline{S T}\) is 22 in,

Explanation:
Given side length of triangle SRT as SR 8 in. and RT as 20 in. as triangle is right triangle applying
Pythagorean theorem to find the length of ST as ST² = 8² + 20²,
ST² = 64 + 400 = 464, So ST is equal to square root of 464 = 21.54 nearly 22 in.

Question 9.
The steps shown can be used to prove the Pythagorean Theorem.

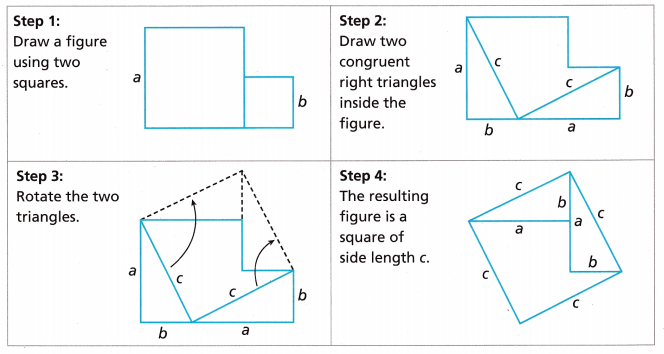
Explain how the steps prove the Pythagorean Theorem. Hint: Write expressions for the total area of the figures in Step 1 and in Step 4.
Answer:
c² = a² + b² ,

Explanation:
Asking to prove the Pythagorean Theorem as a² + b² = c², So
Step 1: Drawn a figure using two squares one big square with side a we have area of
square as a² and small square with side b and area as b², total area is a² + b².
Step 2: Drawn two congruent right triangles inside the figure as shown above with hypotenuse as c,
Step 3: Rotated the two triangles as shown above,
Step 4: The resulting figure is a square of side length c.
Therefore the area of resulting sqaure is a² + b² = c² which is equal to a² + b². hence proved.

Question 10.

Which set of side lengths could form a right triangle?
(A) 3ft, 5ft, 12ft
(B) 5ft, 12ft, 13ft
(C) 12ft, 13ft, 16ft
(D) 13ft, 16ft, 24ft
Answer:
(B) 5ft, 12ft, 13ft,

Explanation:
To find which set of side lengths could form a right triangle is checking with bit(A) 3ft, 5ft, 12ft we have (3)² + (5)² = 12², 9 + 25 = 144, as 34 ≠ 144, checking with bit (B) 5ft, 12ft, 13ft we have
(5)² + (12)² = 13², 25 + 144 = 169, as 169 =169, checking with bit(C) 12ft, 13ft, 16ft we have
(12)² + (13)² = 16², 144 + 169 = 256, as 313 ≠ 256, now checking with bit(D) 13ft, 16ft, 24ft we have
(13)² + (16)² = 24², 169 + 256 = 576, as 425 ≠ 576, therefore bit (B) lengths could form a right triangle.

Question 11.
Meg is making a scale model of an Egyptian pyramid. The model is a right square pyramid as shown. To the nearest centimeter, what is the base length b of the model?

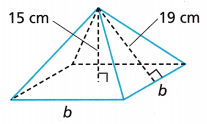
(A) 12 cm
(B) 16 cm
(C) 23 cm
(D) 48 cm
Answer:
(A) 12 cm,

Explanation:
Given Meg is making a scale model of an Egyptian pyramid. The model is a right square pyramid as shown above. The nearest centimeter is the base length b of the model is as it is right triangle applying Pythagorean theorem as19² = b² + 15², b² = 361 – 225 = 136, So b is equal to square root of
11.66 nearly 12 cm which matches with bit (A).

For Problems 12-14, determine the distance between the pair of points, to the nearest hundredth of a unit.

Question 12.
A(-2, 1) and B(3, 5) ________________ units
Answer:
Distance between A and B is approximately 6 units,

Explanation:
Given A(-2, 1) and B(3, 5) the distance between the pair of points be x so applying Pythagorean theorem as x² = (3 – (-2))² + (5 – 1)², x² = 25 + 16 = 41, So x is equal to square root of
41 = 6.40 nearly 6 units.

Question 13.
C(-5, -2) and D(0, -4) _______________ units
Answer:
Distance between C and D is approximately 5 units,

Explanation:
Given C(-5, -2) and D(0, -4) the distance between the pair of points be x so applying Pythagorean theorem as x² = (0 – (-5))² + (-4 – (-2))², x² = 25 + 4 = 29, So x is equal to square root of
29 = 5.38 nearly 5 units.

Question 14.
E(7, 3) and F(-2, 6) _______________ units
Answer:
Distance between E and F is approximately 9 units,

Explanation:
Given E(7, 3) and F(-2, 6) the distance between the pair of points be x so applying Pythagorean theorem as x² = (-2 – 7)² + (6 – 3)², x² = 81 + 9 = 90, So x is equal to square root of
90 = 9.48 nearly 9 units.