We included HMH Into Math Grade 8 Answer Key PDF Module 11 Lesson 4 Apply the Pythagorean Theorem in the Coordinate Plane to make students experts in learning maths.
HMH Into Math Grade 8 Module 11 Lesson 4 Answer Key Apply the Pythagorean Theorem in the Coordinate Plane
I Can apply the Pythagorean Theorem to find the lengths of line segments on the coordinate plane, including line segments that are part of a composite figure.
Step It Out
Question 1.
To find the distance between two points in the coordinate system (on a coordinate plane), draw a right triangle using the horizontal and vertical lines of the grid, with the given points as endpoints of the hypotenuse. Use the Pythagorean Theorem to find the distance between the points.
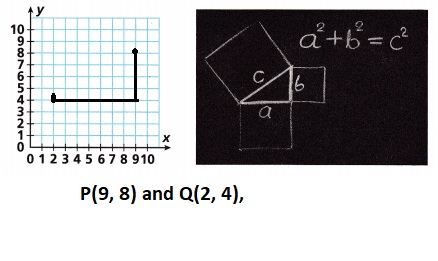
A. Plot the Points P(9, 8) and Q(2, 4), then use a straight edge to draw a line between the points.
Answer:
Explanation:
Plotted the Points P(9, 8) and Q(2, 4), then used a straight edge to draw a line between the points as shown above.
B. Use the horizontal and vertical lines of the coordinate system to draw the legs of a right triangle with Point P and Point Q as vertices.
Answer:
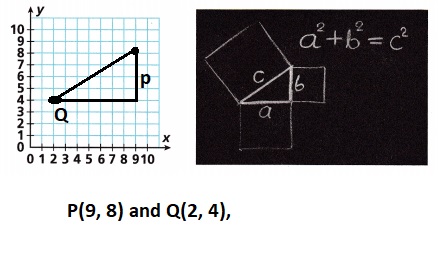
Explanation:
Used the horizontal and vertical lines of the coordinate system to draw the legs of a right triangle
with Point P and Point Q as vertices as shown above.
C. Determine the length of the horizontal and vertical legs, then use the Pythagorean Theorem to determine the length of \(\overline{P Q}\). Round to the nearest tenth.
a2 + b2 = c2
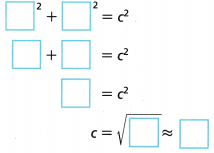
The distance between Points P and Q is approximately ____________ units.
Answer:

The distance between points P and Q is approximately 8 units,
Explanation:
The length of the horizontal and vertical legs, then using the Pythagorean
Theorem to determine the length of \(\overline{P Q}\).
(2 – 9)2 + (4 – 8)2 = PQ2, (-7)2 + (-4)2 = PQ2, 49 + 16 = x2, x2 = 65 , So x is equal to
square root of 65, we get x = 8.062 rounding to the nearest tenth we get 8 units.
Turn and Talk How many right triangles can you draw using a given pair of points as the endpoints of the hypotenuse? Justify your reasoning.
Answer:
The number is infinite,
Explanation:
Let the diameter of a circle be the hypotenuse. At one end of the diameter draw a chord in the semicircle. Doing the same at the other end, but let this chord contact the point on
the semicircle made by the first chord. By Thales Theorem, the figure you’ve drawn
is a right triangle, since all triangles in a semicircle, whose hypotenuse is the diameter of that circle and whose sides are chords of the semicircle.
There will be an infinite number of right triangles in the semicircle as the length of the 2 chords change, while the hypotenuse (diameter) remains unchanged.
Question 2.
Use the Pythagorean Theorem to find the distance between two points on the coordinate plane.
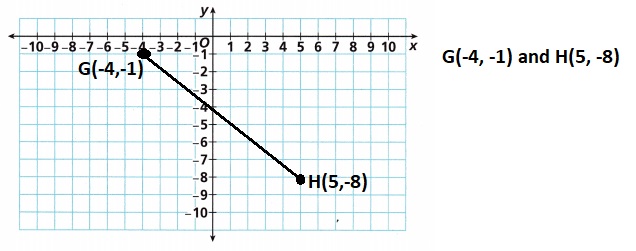
A. In the coordinate plane, graph Points G(-4, -1) and H(5, -8). Draw a line segment connecting the points.
Answer:
Explanation:
Given the coordinate plane graph Points G(-4, -1) and H(5, -8).
Drawn a line segment connecting the points.
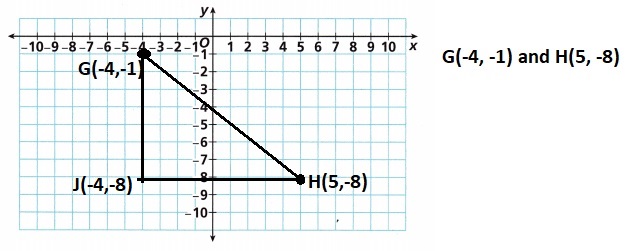
B. Use the horizontal and vertical grid lines to draw the legs of a right triangle with \(\overline{G H}\) as the hypotenuse. Label the point where the legs meet as Point J. Give the coordinates of Point J.
Answer:
Explanation:
Used the horizontal and vertical grid lines to draw the legs of a right triangle with \(\overline{G H}\) as the hypotenuse. Labelled the point where the legs meet as Point J.
The coordinates of Point J are (-4,-8).
C. Determine the length of the horizontal and vertical legs, then use the Pythagorean Theorem to determine the length of GH. Round to the nearest tenth.
a2 + b2 = c2
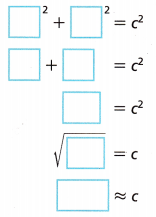
The distance between (-4, -1) and (5, -8) is approximately __________ units.
Answer:
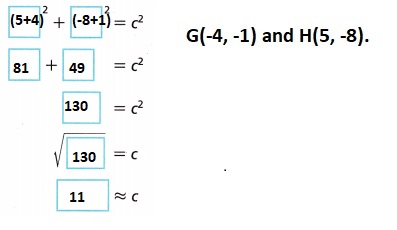
The distance between (-4, -1) and (5, -8) is approximately 11 units,
Explanation:
Determining the length of the horizontal and vertical legs,
then using the Pythagorean Theorem to determine the length of GH,
(5 – (-4))2 + (-8 – (-1))2 = GH2, (9)2 + (-7)2 = GH2, 81 + 49 = GH2,
GH2 = 130 , So GH is equal to square root of 130, we get GH = 11.40 rounding
to the nearest tenth we get 11 units.
Turn and Talk Can a right triangle be formed using any two points on
the coordinate plane? Explain.
Answer:
If the product of slopes of any two sides is equal to -1 other wise they don’t,
Explanation:
Checking whether the product of slopes of any two sides is equal to -1. If the product of slopes of
any two sides is equal to -1, then those two sides are perpendicular and the angle between them is 90°.
Then the given sides form a right triangle, other wise they don’t.
Question 3.
The Purple Movers drew their logo on graph paper. They want to know the perimeter of the design.
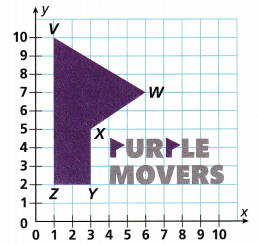
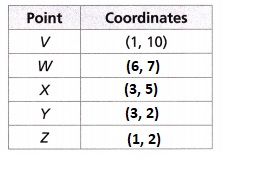
A. Complete the table with the coordinates.
Answer:
Explanation:
Completed the table with the coordinates as shown above.
B. Use the Pythagorean Theorem to calculate the length of \(\overline{V W}\). Round to the nearest tenth.
___________ units
Answer:
The length of \(\overline{V W}\) is 6 units,
Explanation:
We have V as (1,10) and W as (6,7) applying Pythagorean Theorem to calculate the length of
\(\overline{V W}\) as (6 – 1)2 + (7 – 10)2 = VW2, (5)2 + (-3)2 = VW2,
25 + 9 = VW2, VW2 = 34 , So VW is equal to square root of 34, we get VW = 5.83 rounding
to the nearest tenth we get 6 units.
C. Use the same method to determine the length of \(\overline{W X}\). Round to the nearest tenth.
___________ units
Answer:
The length of \(\overline{W X}\) is 4 units,
Explanation:
We have W as (6,7) and X as (3,5) applying
Pythagorean Theorem to calculate the length of
\(\overline{W X}\) as
(3 – 6)2 + (5 – 7)2 = WX2, (-3)2 + (-2)2 = WX2, 9 + 4 = WX2, WX2 = 13 , So WX is equal to
square root of 13, we get WX = 3.60 rounding to the nearest tenth we get 4 units.
D. What is the perimeter of the Purple Movers logo? Round to the nearest tenth.
_____________ units
Answer:
The perimeter of the Purple Movers logo is 23 units,
Explanation:
The perimeter of the Purple Movers logo is the lengths of \(\overline{V W}\) + \(\overline{W X}\) + \(\overline{X Y}\) + \(\overline{Y Z}\) + \(\overline{Z V}\),
As we have lengths of \(\overline{V W}\), \(\overline{W X}\)
calculating lengths of \(\overline{X Y}\), \(\overline{Y Z}\) and
\(\overline{Z V}\),
So length of XY we have X as (3,5) and Y as (3,2) applying Pythagorean Theorem to calculate the length of \(\overline{X Y}\) as (3 – 3)2 + (2 – 5)2 = XY2,
(0)2 + (-3)2 = XY2, 9 = XY2, XY2 = 9 , So XY is equal to square root of 9, we get XY = 3 units.
Now length of YZ we have Y as (3,2) and Z as (1,2) applying Pythagorean Theorem to calculate the length of \(\overline{Y Z}\) as (1 – 3)2 + (2 – 2)2 = YZ2, (-2)2 + (0)2 = YZ2,
4 = YZ2, YZ2 = 4 , So YZ is equal to square root of 4 = 2 units,
Now length of ZV we have Z as (1,2) and V as (1,10) applying Pythagorean Theorem to calculate the length of \(\overline{Z V}\) as (1 – 1)2 + (10 – 2)2 = ZV2, (0)2 + (8)2 = ZV2,
64 = ZV2, So ZV is equal to square root of 64, we get ZV = 8 units.
Therefore the perimeter of the Purple Movers logo is the lengths of
\(\overline{V W}\) + \(\overline{W X}\) + \(\overline{X Y}\) +
\(\overline{Y Z}\) + \(\overline{Z V}\) = 6 + 4 + 3 + 2 + 8 = 23 units,
Check Understanding
Question 1.
On the graph provided, draw a right triangle with Points G and H as endpoints of the hypotenuse. Find the distance between Points G and H. Round to the nearest tenth.
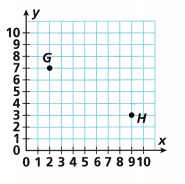
Answer:
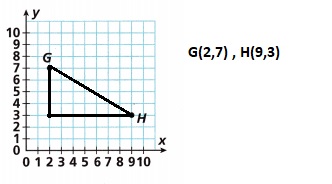
the distance between Points G and H is 8 units,
Explanation:
Given Points G and H as endpoints of the hypotenuse the points are G(2,7), H(9,3) the distance between Points G and H is applying Pythagorean Theorem to calculate the length of
\(\overline{G H}\) as (9 – 2)2 + (3 – 7)2 = GH2, (7)2 + (-4)2 = GH2,
49 + 16 = GH2, GH2 = 65 , So GH is equal to square root of 65, we get GH = 8.06 rounding
to the nearest tenth we get 8 units.
Question 2.
A. On your own paper, plot the points (-2, 6) and (5, -5). Find the distance between these two points. Round to the nearest tenth.
Answer:
The distance between the given points is 13 units,
Explanation:
Given points are (-2, 6) and (5, -5), Let x be the distance between these points so applying Pythagorean theorem as (5 – (-2))2 + (-5 – 6)2 = x2, (7)2 + (-11)2 = x2, 49 + 121 = x2,
x2 = 170 , So x is equal to square root of 170, we get x = 13.03 rounding to the nearest tenth we get 13 units.
B. What is the perimeter of a triangle that has (-2, 6) and (5, -5) as the end points of its hypotenuse? Round to the nearest tenth.
Answer:
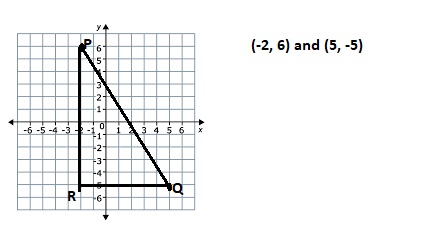
The perimeter of a triangle that has (-2, 6) and (5, -5) as the end points of its hypotenuse is 31 units,
Explanation:
Given points of triangle as (-2, 6) and (5, -5) let it be P and Q now the other point of triangle be R as (-2,-5), Now to find the perimeter of the triangle we find the distance of QR and RP as
for QR (5,-5) and (-2,-5) applying Pythagorean theorem as (-2 – 5)2 + (-5 – (-5))2 = QR2,
(7)2 + (0)2 = QR2, 49 + 0 = QR2, QR2 = 49 , So QR is equal to square root of 49, we get QR = 7 units.
Now RP (-2,-5) and (-2,6) applying Pythagorean theorem as (-2 – (-2))2 + (6 – (-5))2 = RP2,
(0)2 + (11)2 = RP2, 0 + 121 = RP2, RP2 = 121 , So RP is equal to square root of 121, we get RP = 11 units. The perimeter of the triangle = PQ + QR + RP = 13 + 7 + 11 = 31 units.
Question 3.
On your own paper, plot the points (3, 60) and (-5, 45). Find the distance between these two points. Round to the nearest tenth if necessary.
Answer:
The distance between the given points is 17 units,
Explanation:
Given points are (3, 60) and (-5, 45), Let x be the distance between these points so applying Pythagorean theorem as (-5 – 3)2 + (45 – 60)2 = x2, (-8)2 + (-15)2 = x2, 64 + 125 = x2,
x2 = 289 , So x is equal to square root of 289, we get x = 17 units.
On Your Own
Question 4.
Use Structure The town halls of Havertville and Northtown are shown on the map. If the distance between grid lines represents 1 mile, what is the distance between the two town halls? Round your answer to the nearest tenth.
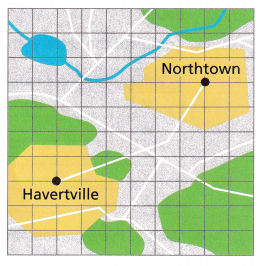
Answer:
The distance between the two town halls is 7 miles,
Explanation:
Let (x, y) be Havertville,
Northtown will be represented as: (x + 6, y + 4) — i.e 6 units right and 4 units up,
So let the distance between both is z, So applying Pythagorean theorem as
(x + 6 – x)2 + (y + 4 – y)2 = z2, (6)2 + (4)2 = z2, 36 + 16 = z2, z2 = 52 , So x is equal to
square root of 52, we get x = 7.211, Round to the nearest tenth we get 7 miles.
Use the graph to answer Problems 5-6.
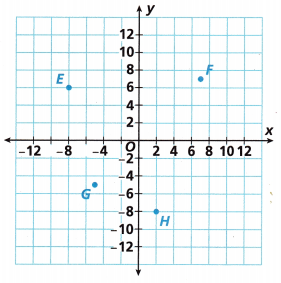
Question 5.
Attend to Precision Which point is exactly 10 units from (0, 0)?
Answer:
Point E is exactly 10 units from (0, 0),
Explanation:
Let (0,0) be point O
Checking (0, 0) with point F(7,7) we have distance as (7 – 0)2 + (7 – 0)2 = OF2,
(7)2 + (7)2 = OF2, 49 + 49 = OF2, OF2 = 98 , So OF is equal to square root of 98, we get OF = 9.89 rounding to the nearest tenth we get 10 units, checking (0,0) with point H(2,-8) we have distance as
(2 – 0)2 + (-8 – 0)2 = OH2, (2)2 + (-8)2 = OH2, 4 + 64 = OH2, OH2 = 68 , So OH is equal to
square root of 68, we get OH = 8.24 rounding to the nearest tenth we get 8 units,
checking (0,0) with point G(-5,-5) we have distance as (-5 – 0)2 + (-5 – 0)2 = OG2,
(-5)2 + (-5)2 = OG2, 25 + 25 = OG2, OG2 = 50 , So OG is equal to square root of 50, we get OG = 7.07 rounding to the nearest tenth we get 7 units, checking (0,0) with point E(-8,6) we have distance as
(-8 – 0)2 + (6 – 0)2 = OE2, (-8)2 + (6)2 = OE2, 64 + 36 = OE2, OE2 = 100, So OE is equal to
square root of 100, we get OE = 10 units, therefore point E is exactly 10 units from (0, 0).
Question 6.
What is the distance between Points E and H? Round to the nearest tenth.
__________ units
Answer:
The distance between Points E and H is 17 units,
Explanation:
The distance between points E(-8,6) and H(2, -8) is (2 – (-8))2 + (-8 – 6)2 = EH2,
(10)2 + (-14)2 = EH2, 100 + 196 = EH2, EH2 = 296 , So EH is equal to square root of 296,
we get EH = 17.20 rounding to the nearest tenth we get 17 units.
Question 7.
On your own paper, graph the points (-5, 4) and (4, 2). Use the grid lines to draw a right triangle with the given points as endpoints of the hypotenuse.
A. Give the two possible coordinates of the third vertex.
Answer:
The two possible coordinates of the third vertex are (-5,2) and (4,4),
Explanation:
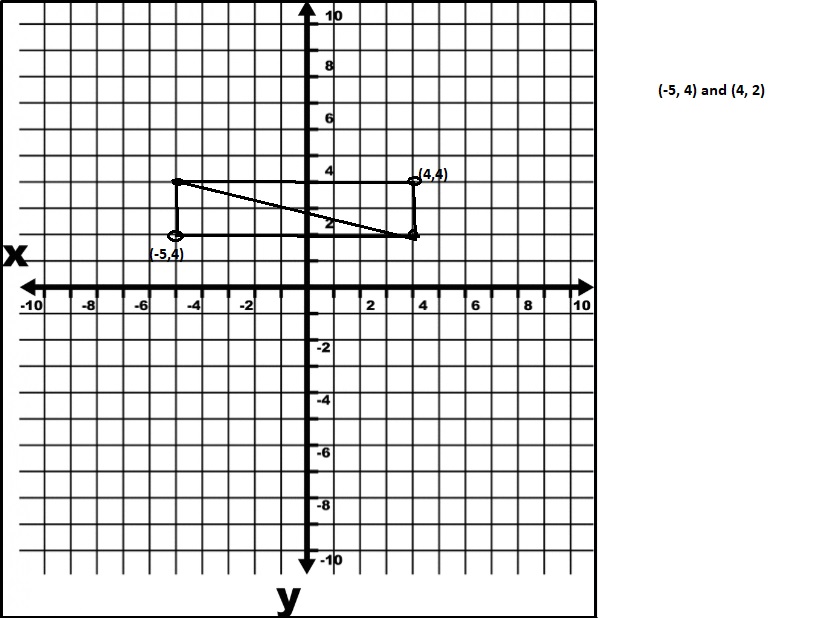
If we see the graph the two possible coordinates of the third vertex are (-5,2) and (4,4).
B. Find the distance between the given points. Round to the nearest tenth of a unit.
Answer:
The distance between the given points is 9 units,
Explanation:
Let x be the distance between the given points (-5, 4) and (4, 2), so (4 – (-5))2 + (2 – 4)2 = x2,
(9)2 + (-2)2 = x2, 81 + 4 = x2, x2 = 85 , So x is equal to square root of 85, we get x = 9.21 rounding
to the nearest tenth we get 9 units.
C. Find the perimeter of the triangle to the nearest tenth of a unit.
Answer:
The perimeter of the triangle 20 units,
Explanation:
Let the ponits be P (-5, 4), Q (4, 2) and R(-5,2),
the distance between QR is (-5 – 4)2 + (2 – 2)2 = QR2,
(-9)2 + (0)2 = QR2, 81 + 0 = QR2, QR2 = 81 , So QR is equal to square root of 81, we get QR = 9 units,
Now (-5 – (-5))2 + (4 – 2)2 = RP2, (0)2 + (2)2 = RP2, 0 + 4 = RP2,
RP2 = 4 , So RP is equal to square root of 4, we get RP = 2 units,
Therefore the perimeter of the triangle is 9 + 9 + 2 = 20 units.
Question 8.
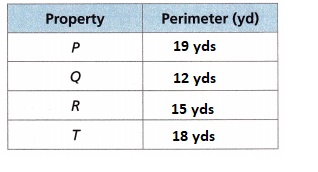
A fencing company is putting fences around the properties shown on the map. Each unit on the map is 1 yard. They need to decide which property has the longest perimeter so they know which will require the most fencing.
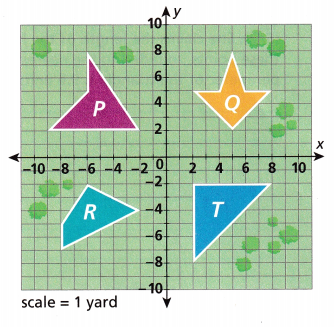
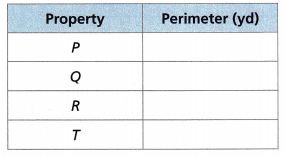
A. Complete the table with the perimeters of each of the properties. Round to the nearest tenth.
Answer:
Explanation:
Given a fencing company is putting fences around the properties shown on the map. Each unit on the map is 1 yard. They need to decide which property has the longest perimeter,
so they know which will require the most fencing. For P we have 6 yds + 3 yds + 3 yds + 7 yds = 19 yds, Q we have 3 yds + 3 yds + 3 yds + 3 yds = 12 yds, For R we have 6 yds + 4 yds + 3 yds + 2 yds = 15 yds, for T we have 6 yds + 6 yds + 6 yds = 18 yds,
Completed the table with the perimeters of each of the properties as shown above.
B. The property with the shortest perimeter is _____________.
Answer:
The property with the shortest perimeter is Q,
Explanation:
If we see the perimeters 12 yds < 15 yds < 18 yds < 19 yds,
Q < R < T < P as Q is having least perimeter so the shortest perimeter is Q.
C. The property with the longest perimeter is ______________.
Answer:
The property with the longest perimeter is P,
Explanation:
If we see the perimeters 19 yds > 18 yds > 15 yds > 12 yds, P > T > R > Q as P is having larger perimeter so the longest perimeter is P.
Question 9.
Use Tools On your own paper, graph the points (-8, 7) and (-5, -4). Use the grid lines to draw a right triangle with the given points as endpoints of the hypotenuse.
A. Give two possible coordinate pairs for the third vertex.
Answer:
The two possible coordinates of the third vertex are (-8,-4) and (-5,7),
Explanation:
Given points are (-8, 7) and (-5, -4), So the two possible
coordinates of the third vertex are (-8,-4) and (-5,7).
B. Find the distance between the given points. Round to the nearest tenth.
Answer:
The distance between the given points is 11 units,
Explanation:
Let x be the distance between the given points (-8, 7) and (-5, -4),
so (-5 – (-8))2 + (-4 – 7)2 = x2, (3)2 + (-11)2 = x2, 9 + 121 = x2,
x2 = 130 , So x is equal to square root of 130, we get x = 11.40 rounding
to the nearest tenth we get 11 units.
C. What is the perimeter of the triangle you drew?
Answer:
The perimeter of the triangle is 25 units,
Explanation:
If we take points as P(-8, 7), Q(-5, -4) and R(-8,-4), The distance between QR is
(-8 – (-5))2 + (-4 – (-4))2 = QR2, (-3)2 + (0)2 = QR2, 9 + 0 = QR2, QR2 = 9 , So QR is equal to
square root of 9, we get QR = 3 units. Now the distance between RP is
(-8 – (-8))2 + (7 – (-4))2 = RP2, (0)2 + (11)2 = RP2, 0 + 121 = RP2,
RP2 = 121 , So RP is equal to square root of 121, we get RP = 11 units.
Therefore the perimeter of the triangle = distance of PQ + distance of QR + distance of RP =
11 + 3 + 11 = 25 units.
D. Reason Does your answer change depending on which of the two possible third vertices you chose? Explain.
Answer:
No, the answer will not change depending on which of the two possible third vertices I chose,
Explanation:
If we take points as P(-8, 7), Q(-5, -4) and R(-5,7), Now the distance between QR is
(-5 – (-5))2 + (7 – (-4))2 = QR2, (0)2 + (11)2 = QR2, 0 + 121 = QR2, QR2 = 121 , So QR is equal to
square root of 121, we get QR = 11 units. Now the distance between RP is
(-8 – (-5))2 + (7 – 7)2 = RP2, (-3)2 + (0)2 = RP2, 9 + 0 = RP2,
RP2 = 9 , So RP is equal to square root of 9, we get RP = 3 units.
Therefore the perimeter of the triangle = distance of PQ + distance of QR + distance of RP =
11 + 11 + 3 = 25 units. Therefore, the answer will not change depending on which of the two possible third vertices I chose,
Question 10.
Critique Reasoning Elena plots the points (1, -1), (1, 2), and (5, 2). She claims the length of the hypotenuse of the triangle formed by these points, rounded to the nearest tenth, is equal to 2.6 units, and the perimeter of the triangle is 9.6 units. Is Elena correct? How do you know?
Answer:
Elena is incorrect as hypotenuse of the tiangle is 5 units not 2.6 units and
the perimeter of the triangle is 12 units not 9.6 units,
Explanation:
Given Elena plots the points (1, -1), (1, 2), and (5, 2).
She claims the length of the hypotenuse of the triangle formed by these points, rounded to the nearest tenth is equal to 2.6 units, and the perimeter of the triangle is 9.6 units.
Plotting the graph
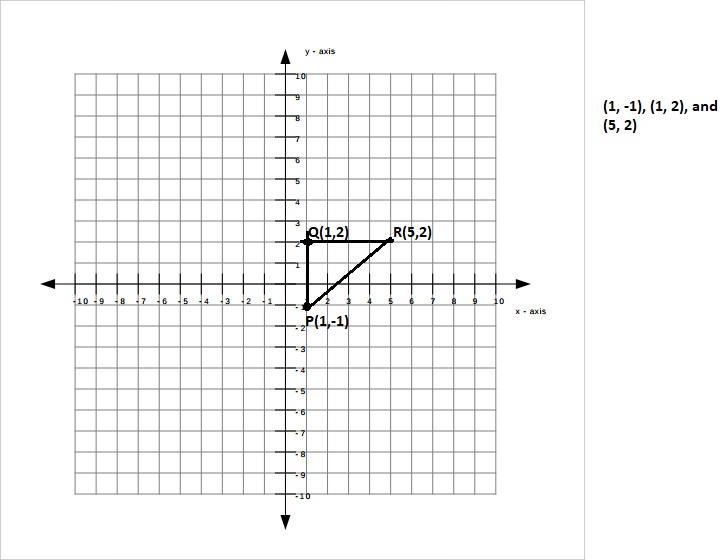
let the points be P(1, -1), Q(1, 2), and R(5, 2),
the length of the hypotenuse of the triangle formed by these points is PR,
Now the distance between PR is (5 – 1)2 + (2 – (-1))2 = PR2,
(4)2 + (3)2 = PR2, 16 + 9 = PR2, PR2 = 25 , So PR is equal to square root of 25, we get PR = 5 units.
Now perimeter of triangle is first the distance between PQ is (1 – 1)2 + (2 – (-1))2 = PQ2,
(0)2 + (3)2 = PQ2, 0 + 9 = PQ2, PQ2 = 9 , So PQ is equal to square root of 9, we get PQ = 3 units.
Now the distance between QR is (5 – 1)2 + (2 – 2)2 = QR2, (4)2 + (0)2 = QR2,
16 + 0 = QR2, QR2 = 16, So QR is equal to square root of 16, we get QR = 4 units.
So the perimeter of triangle is 5 + 3 + 4 = 12 units. Therefore Elena is incorrect as hypotenuse of the tiangle is 5 units not 2.6 units and the perimeter of the triangle is 12 units not 9.6 units,
Question 11.
Georgia placed a grid over the map of the post office and the local library.
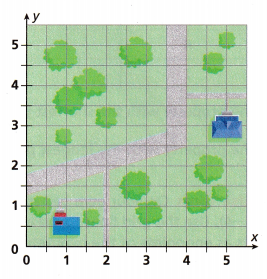
A. Give the coordinates of the post office and the library.
Answer:
Coordinates of the post office is (1,0.5) and the library is (5,3),
Explanation:
Given Georgia placed a grid over the map of the post office and the local library.
So the coordinates of the post office is (1,0.5) and the library is (5,3).
B. If each grid mark represents 0.5 mile, find the distance between the two buildings.
Round to the nearest hundredth.
Answer:
The distance between the two buildings is 5 miles,
Explanation:
B. If each grid mark represents 0.5 mile, The distance between the two buildings (1,0.5) and (5,3) is
(5 – 1)2 + (3 – 0.5)2, (4)2 + (2.5)2, 16 + 6.25, 22.25, So the distance is equal to square root of 22.5,
we get 4.71 units nearer to 5 miles.
Question 12.
Ali drew the 3-pointed star shown on the graph.
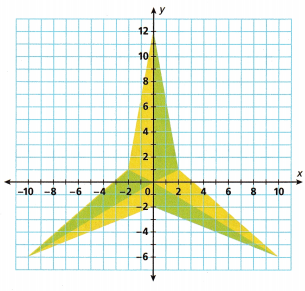
A. What is the perimeter of this 3-pointed star? Round to the nearest tenth.
Answer:
The perimeter of the 3 -pointed star is 84 units,
Explanation:
Given Ali drew the 3-pointed star shown on the graph the right angle triangles are
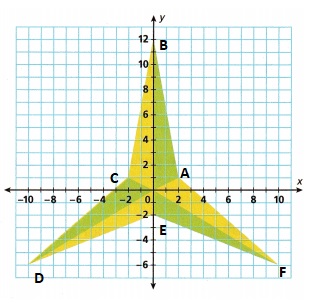
OAB,OCB,OCD,ODE,OEF and OFA
We have points of OAB as O(0,0), A(2,1) and B(0,12) the distance of AB is distance of OA + distance of OB = (2 – 0)2 + (1 – 0)2 = OA2, (2)2 + (1)2 = OA2, 4 + 1 = OA2, OA2 = 5, So OA = 2.23 nearly 2,
Now OB2 = (0 – 0)2 + (12 – 0)2 , OB2 = (0)2 + (12)2, OB2 = 0 + 144 = 144, OB is square root of 144 = 12,
So AB = 2 + 12 = 14, Now we have points of OCB as O(0,0), C(-2,1) and B(0, 12),
the distance of BC is distance of OC + distance of OB, OC2 = (-2 – 0)2 + (1 – 0)2 ,
OC2 = (-2)2 + (1)2, OC2 = 4 + 1 = 5, OC is square root of 5 = 2.23 nearly 2,
As the distance of OB is 12, so distance of BC is 2 + 12 = 14,
Now we have points of OCD as O(0,0), C(-2,1) and D(-10,-6)
the distance of CD is distance of OC + distance of OD = (-2 – 0)2 + (1 – 0)2 = OC2,
(-2)2 + (1)2 = OC2, 4 + 1 = OC2, OC2 = 5, So OC = 2.23 nearly 2,
Now OD2 = (-10 – 0)2 + (-6 – 0)2 , OD2 = (-10)2 + (-6)2,
OD2 = 100 + 36 = 136, OD is square root of 136 = 11.66 nearly 12,
So CD = 2 + 12 = 14,
Now we have points of ODE as O(0,0), D(-10,-6) and E(0,-2),
The distance of DE is distance of OD + distance of OE,
OE2 = (0 – 0)2 + (-2 – 0)2 , OE2 = (0)2 + (-2)2, OE2 = 0 + 4 = 4, OE is square root of 4 = 2,
we have distance of OD as 12 so distance of DE is 12 + 2 = 14,
Now we have points of OEF as O(0,0), E(0,-2) and F(10,-6)
the distance of EF is distance of OE + distance of OF = (0 – 0)2 + (-2 – 0)2 = OE2,
(0)2 + (-2)2 = OE2, 0 + 4 = OE2, OE2 = 4, So OE = 2, Now OF2 = (10 – 0)2 + (-6 – 0)2 ,
OF2 = (10)2 + (-6)2, OF2 = 100 + 36 = 136, OF is square root of 136 = 11.66 nearly 12,
So EF = 2 + 12 = 14, Now we have points of OFA as O(0,0), F(10,-6) and A(2,1)
the distance of AF is distance of OF + distance of OA = as we have distance of OF as 12 and distance of OA as 2 so distance of AF is 12 + 2 = 14, The perimeter of the 3 -pointed star is
distances of (AB + BC + CD + DE + EF + AF) = 14 + 14 + 14 + 14 + 14 + 14 = 84 units.
B. Explain how you used right triangles to find the perimeter.
Answer:
Added all distances of hypotenuse of each right triangles,
Explanation:
To find the perimeter of 3-pointed star I added hypotenuse distance of all right triangles as
for right triangle OAB distance of hypotenuse AB, for right triangle OCB distance of hypotenuse BC,
for right triangle OCD distance of hypotenuse CD for right triangle ODE distance of hypotenuse DE,
for right triangle OEF distance of hypotenuse EF for right triangle OFA distance of hypotenuse AF respectively.
Lesson 11.4 More Practice/Homework
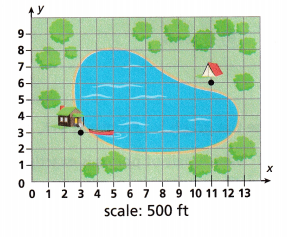
Question 1.
Renee takes a boat directly from the lodge to the campsite. If the distance between grid lines represents 500 feet, how far does Renee travel? Round to the nearest 10 feet.
Answer:
Renee travelled 4,500 feet,
Explanation:
Given Renee takes a boat directly from the lodge to the campsite. If the distance between
grid lines represents 500 feet, Renee travel let A be point of lodge as (3,3) and B be the point of campsite as (11,6), so the distance is AB2 = (11 – 3)2 + (6 – 3)2 , AB2 = (8)2 + (3)2,
AB2 = 64 + 9 = 73, AB is square root of 73 = 8.54 nearly 9, So 9 X 500 = 4,500 feet Renee travelled.
Question 2.
Use Tools On your own paper, plot the Points E(-2, 2) and F(8, 10). Use the vertical and horizontal grid lines to draw a right triangle with these two points as vertices.
A. Label the third vertex of your right triangle Point G. Identify the two possible coordinates of Point G.
Answer:
The two possible coordinates of Point G are (8,2) or (-2,10),
Explanation:
Given the points E(-2, 2) and F(8, 10), So the two possible coordinates of Point G are (8,2) or (-2,10).
B. What is the distance between Points E and F? Round to the nearest tenth of a unit.
Answer:
The distance between Points E and F is 13 units,
Explanation:
The distance between Points E(-2,2) and F(8,10) is EF2 = (8 – (-2))2 + (10 – 2)2 ,
EF2 = (10)2 + (8)2, EF2 = 100 + 64 = 164, EF is square root of 164 = 12.80 nearly 13 units.
C. What it the perimeter of AEFG? Round to the nearest tenth of a unit.
Answer:
The perimeter of triangle EFG is 31 units,
Explanation:
The perimeter of triangle EFG with points E(-2, 2), F(8, 10) and G(8,2) is
distance of EF + distance of EG + distance of FG, We already have distance of EF as 13 units,
So distance of EG is EG2 = (8 – (-2))2 + (2 – 2)2 , EG2 = (10)2 + (0)2,
EG2 = 100 + 0 = 100, EG is square root of 100 = 10 units.
Now distance of FG is FG2 = (8 – 8)2 + (2 – 10)2 , FG2 = (0)2 + (-8)2,
FG2 = 0 + 64 = 64, FG is square root of 64 = 8 units.
Therefore perimeter of triangle EFG is 13 + 10 + 8 = 31 units.
Question 3.
Use Tools On your own paper, graph the points (-2, -4) and (4, -1). Use the grid lines to draw a right triangle with the given points as endpoints of the hypotenuse.
A. Give a possible coordinate pair of the third vertex.
Answer:
Coordinate pair of the third vertex is (-2,-1),
Explanation:
Given the points (-2, -4) and (4, -1) so the possible
coordinate pair of the third vertex is (-2,-1).
B. What is the vertical distance between the points? What is the horizontal distance between the points?
Answer:
The vertical distance between the points is 3 units,
The horizontal distance between the points is 6 units,
Explanation:
Let the vertical distance be V between the points (-2,-1) and (-2,-4) is
V2 = (-2 – (-2))2 + (-4 – (-1))2, V2 = (0)2 + (-3)2, V2 = 0 + 9 = 9, So V is square root of 9 = 3 units.
Let the horizontal distance be H between the points (-2,-1) and (4,-1) is
H2 = (4 – (-2))2 + (-1 – (-1))2, H2 = (6)2 + (0)2, H2 = 36 + 0 = 36, So H is square root of 36 = 6 units.
C. Find the distance between the given points. Round to the nearest tenth of a unit.
Answer:
The distance between the given points is 7 units
Explanation:
Let X be the distance between the given points (-2, -4) and (4, -1) is
X2 = (4 – (-2))2 + (-1 – (-4))2, X2 = (6)2 + (3)2,
X2 = 36 + 9 = 45, So X is square root of 45 = 6.708 nearly 7 units.
D. What is the perimeter of the triangle you drew? Round to the nearest tenth of a unit.
Answer:
The perimeter of the triangle I drew is 16 units,
Explanation:
The perimeter of the triangle I drew is distance of X + distance of V + distance of H,
so 7 units + 3 units + 6 units = 16 units.
Question 4.
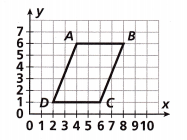
Test Prep
What is the direct distance between Point A and Point C on Parallelogram ABCD?
(A) 4.8 units
(B) 5 units
(C) 5.2 units
(D) 5.4 units
Answer:
(D) 5.4 units,
Explanation:
The direct distance between Point A and Point C on Parallelogram ABCD is
we have point A as (4,6) and point C as (6,1), So AC2 = (6 – 4)2 + (1 – 6)2,
AC2 = (2)2 + (-5)2, AC2 = 4 + 25 = 29, So AC is square root of 29 = 5.38
nearly 5.4 units matches with bit (D).
Use the graph for Problems 5-7.
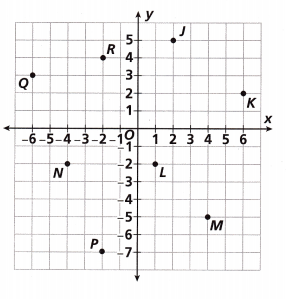
Question 5.
Which pair of points is exactly 5 units apart?
(A) J and K
(B) L and M
(C) N and P
(D) Q and R
Answer:
(A) J and K,
Explanation:
Checking with bit (A) J and K as J is (2,5) and K is (6,2),
So distance of JK is JK2 = (6 – 2)2 + (2 – 5)2,
JK2 = (4)2 + (-3)2,
JK2 = 16 + 9 = 25, So JK is square root of 25 = 5 units,
Checking with bit (b) L and M as L is (1,-2) and M is (4,-5),
So distance of LM is LM2 = (4 – 1)2 + (-5 – (-2))2, LM2 = (3)2 + (-3)2,
LM2 = 9 + 9 = 18, So LM is square root of 18 = 4.24 nearly 4 units,
Checking with bit (C) N and P as N is (-4,-2) and P is (-2,-7),
So distance of NP is NP2 = (-2 -(-4))2 + (-7 – (-2))2,
NP2 = (2)2 + (-5)2, NP2 = 4 + 25 = 29, So NP is square root of 29 = 5.38 nearly 5 units,
Checking with bit (D) Q and R as Q is (-6,3) and R is (-2,4),
So distance of QR is QR2 = (-2 – (-6))2 + (4 – 3)2, QR2 = (4)2 + (1)2,
QR2 = 16 + 1 = 17, So QR is square root of 17 = 4.12 nearly 4 units,
Therefore only bit (A) J and K matches with exactly 5 units apart.
Question 6.
How far apart are L and M?
(A) 6 units
(B) \(\sqrt {9}\) units
(C) \(\sqrt {12}\) units
(D) \(\sqrt {18}\) units
Answer:
(D) \(\sqrt {18}\) units,
Explanation:
As L and M as L is (1,-2) and M is (4,-5), The distance of LM is LM2 = (4 – 1)2 + (-5 – (-2))2,
LM2 = (3)2 + (-3)2, LM2 = 9 + 9 = 18, So LM is square root of 18 which matches
with bit (D).
Question 7.
Which pair of points is \(\sqrt {29}\) units apart?
(A) J and L
(B) P and M
(C) N and P
(D) Q and R
Answer:
(C) N and P,
Explanation:
The pair of points is \(\sqrt {29}\) units apart are Checking with bit (A) J and L as J is (2,5) and L is (1,-2), So distance of JL is JL2 = (1 – 2)2 + (-2 – 5)2,
JK2 = (-1)2 + (-7)2, JK2 = 1 + 49 = 50, So JL is square root of 50 units,
Checking with bit (b) P and M as P is (-2,-7) and M is (4,-5),
So distance of PM is PM2 = (4 – (-2))2 + (-5 – (-7))2, PM2 = (6)2 + (2)2,
PM2 = 36 + 4 = 40, So PM is square root of 40 units, Checking with bit (C)
N and P as N is (-4,-2) and P is (-2,-7), So distance of NP is NP2 = (-2 -(-4))2 + (-7 – (-2))2,
NP2 = (2)2 + (-5)2, NP2 = 4 + 25 = 29, So NP is square root of 29 units,
Checking with bit (D) Q and R as Q is (-6,3) and R is (-2,4),
So distance of QR is QR2 = (-2 – (-6))2 + (4 – 3)2, QR2 = (4)2 + (1)2,
QR2 = 16 + 1 = 17, So QR is square root of 17 units, therefore bit (C) N and P matches with the pair of points is \(\sqrt {29}\) units apart.
Question 8.
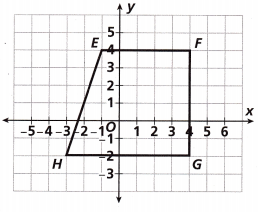
What is the perimeter of Trapezoid EFGH?
(A) 24 units
(B) 24.3 units
(C) 25 units
(D) 25.3 units
Answer:
(B) 24.3 units,
Explanation:
Given to find the perimeter of Trapezoid EFGH,
So it is distances of (EF + FG + GH + HE), We have E as (-1,4) and F as (4,4),
the distance of EF is EF2 = (4 – (-1))2 + (4 – 4)2, EF2 = (5)2 + (0)2,
EF2 = 25 + 0 = 25, So EF is square root of 25 = 5 units, We have F as (4,4) and G as (4,-2),
the distance of FG is FG2 = (4 – 4)2 + (-2 – 4)2, FG2 = (0)2 + (-6)2,
FG2 = 0 + 36 = 36, So FG is square root of 36 = 6 units, We have G as (4,-2) and H as (-3,-2),
the distance of GH is GH2 = (-3 – 4)2 + (-2 – (-2))2, GH2 = (-7)2 + (0)2,
GH2 = 49 + 0 = 49, So GH is square root of 49 = 7 units,
We have H as (-3,-2) and E as (-1,4), the distance of HE is HE2 = (-1 – (-3))2 + (4 – (-2))2,
HE2 = (2)2 + (6)2, HE2 = 4 + 36 = 40, So HE is square root of 40 = 6.32 nearly 6.3 units,
Now the perimeter of Trapezoid EFGH is 5 units + 6 units + 7 units + 6.3 units = 24.3 units
which matches with bit(B) 24.3 units.
Spiral Review
Question 9.
Find the value of x that makes the equation true.
12x = 4(x + 2) + 20
Answer:
The value of x is 3.5,
Explanation:
Given to find the value of x that makes the equation true 12x = 4(x + 2) + 20, Solving 12x = 4x + 8 + 20, 12x = 4x + 28, 12x – 4x = 28, 8x = 28, therefore x = \(\frac{28}{8}\) = 3.5.
Question 10.
A line has a slope of 8 and crosses the y-axis at (0, 12). Express this line in slope-intercept form.
Answer:
y = 8x + 12,
Explanation:
Given a line has a slope of 8 and crosses the y-axis at (0, 12).
As we have the equation for all linear equations (slope-intercept form) is y = mx + b
where m = slope and b = the y-intercept.
Expressing this line in slope-intercept form as m is 8 and y- intercept is 12 that is constant b is y = 8x + 12.