Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem

We included HMH Into Math Grade 8 Answer Key PDF Module 11 Lesson 3 Apply the Pythagorean Theorem to make students experts in learning maths.

HMH Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem

I Can apply the Pythagorean Theorem to solve real-life problems involving the legs and hypotenuse of a right triangle, including problems in three dimensions.

Step It Out

Question 1.
The red team and blue team are playing Capture the Flag. Each team places their flag at opposite corners of the field. The red team sends two players, Alfredo and Angelina, from the red flag to capture the blue flag.
$HMH Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem 1$
A. Alfredo must follow the white arrows to the flag. How far does he run?
$HMH Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem 2$
Alfredo runs ___________ meters.
Answer:
150 m + 85 m = 235 meters, Alfredo runs 235 meters,

Explaantion:
Given the red team and blue team are playing capture the Flag. Each team places their flag at opposite corners of the field. The red team sends two players, Alfredo and Angelina, from the red flag to capture the blue flag. Alfredo must follow the white arrows to the flag so far
does he runs is 150 m + 85 m = 235 meters, Alfredo runs 235 meters.

B. Angelina must follow the black arrow to the flag. Use the Pythagorean Theorem to determine how far she runs. Round to the nearest tenth.
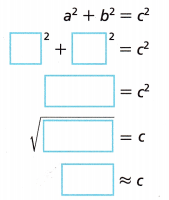
$HMH Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem 3$
Angelina runs __________ meters.
Answer:
$Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem-1$
Angelina runs 172 meters,

Explanation:
Given Angelina must follow the black arrow to the flag.
Using the Pythagorean Theorem to determine how far she runs.
a² + b² = c², 150² + 85² = c², 22,500 + 7,225 = c², c²= 29,725, So c is equal to sqaure root of 29,725 we get c = 172.4 round to the nearest tenth is 172. Therefore Angelina runs 172 meters.

C. How much farther does Alfredo run than Angelina?
$HMH Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem 2$
Alfredo runs ___________ meters farther than Angelina.
Answer:
Alfredo runs 63 meters farther than Angelina,

Explanation:
Farther does Alfredo run than Angelina as Alfredo runs 235 meters and Angelina runs 172 meters
is 235 – 172 = 63 meters.

Turn and Talk Will the direct route always be shorter than a route between two points with a right angle? Why or why not?
Answer:
No,

Explanation:
A direct route isn’t always the shortest distance between two points with a right angle,
The shortest distance between two points with a right angle depends on the geometry of the object/surface in question.

The Pythagorean Theorem can be used to find lengths inside a three-dimensional object by finding right triangle relationships inside the object.

Question 2.
Jada wants to ship a 3-foot curtain rod to a customer. The biggest box at the post office is shown. Jada wants to know if the box is large enough to ship the curtain rod.
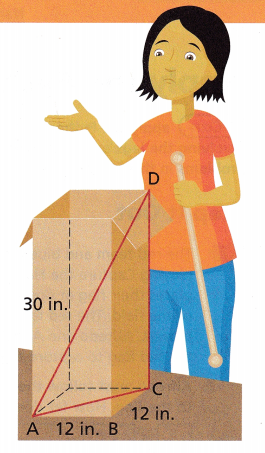
$HMH Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem 4$
A. The longest distance in the box is the diagonal AD between opposite corners.
It forms the hypotenuse of ∆ACD.
What is the length of $\overline{D C}$ ? ____________ inches
Answer:
The length of $\overline{D C}$ is 30 inches,

Explanation:
As given the length of $\overline{D C}$ is 30 inches.

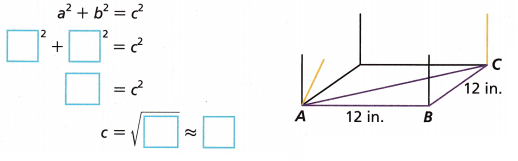
B. To find the length of $\overline{A B}$ we must know the length of $\overline{A C}$ . Look at the bottom of the box. $\overline{A C}$ is the hypotenuse of another right triangle, ∆ABC. Use the Pythagorean Theorem to find the length of $\overline{A C}$ . Round to the nearest tenth if necessary.
$HMH Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem 5$
Answer:
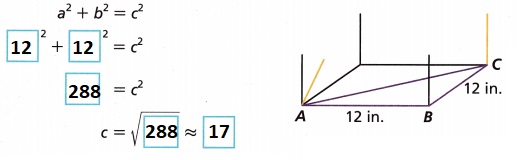
$Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem-2$
The length of $\overline{A C}$ = 17 inches,

Explanation:
To know the length of $\overline{A C}$. Looking at the bottom of the box. $\overline{A C}$ is the hypotenuse of another right triangle, ∆ABC.
Using the Pythagorean Theorem to find the length of
$\overline{A C}$ as a² + b² = c², 12² + 12² = ac²,
144 + 144 = $\overline{A C}$², $\overline{A C}$²= 288, So ac is equal to
sqaure root of 288, we get $\overline{A C}$ = 16.97,
rounding to the nearest tenth we get $\overline{A C}$ = 17.

C. Use the length of $\overline{A C}$ to find the length of $\overline{A D}$. Round to the nearest tenth of an inch.
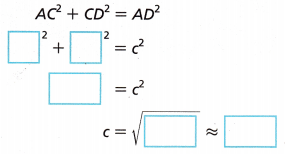
$HMH Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem 6$
The length of $\overline{A D}$ is about _____________ inches.
Answer:
$Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem-3$
The length of $\overline{A D}$ is about 34 inches,

Explanation:
As we have $\overline{A C}$ = 17 inches and the length of $\overline{D C}$ is 30 inches, So the length of $\overline{A D }$ is 17² + 30² = ad²,
289 + 900 = $\overline{A D}$², $\overline{A D}$²= 1,189, So ad is equal to
sqaure root of 1,189, we get $\overline{A D}$ = 34.48, rounding to the nearest tenth we get $\overline{A D}$ = 34 inches.

D. About how long is the longest rod that could fit in the box?
___________ inches
Answer:
About 34 inches,

Explanation:
As we have the longest distance in the box is the diagonal AD between opposite corners.
It forms the hypotenuse of ∆ACD. So we have $\overline{A D}$ = 34 inches, therefore
34 inches is the longest rod that could fit in the box.

E. Can the curtain rod fit in the box? Why or why not?
Answer:
No,

Explanation:
As Jada wants to ship a 3-foot curtain rod to a customer, 3 foot, as 1 foot is equal to 12 inches so 3 foot means 3 X 12 = 36 inches, As the longest rod that could fit in the box is
only 34 inches and we the curtain rod is 36 inches which is greater, So the curtain rod will not fit in the box.

Question 3.
Cara measured the radius and outside length of an ice cream cone. Identify the right triangle in the cone, then use Cara’s measurements to find the height of the cone. Round your final answer to the nearest hundredth.
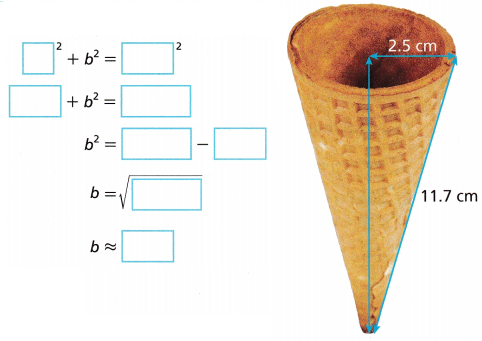
$HMH Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem 7$
The height of the cone is about ______________ centimeters.
Answer:
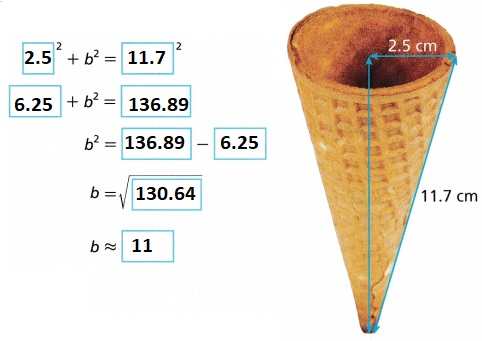
$Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem-4$
The height of the cone is about 11 centimeters,

Explanation:
Given Cara measured the radius and outside length of an ice cream cone. Identified the right triangle in the cone, then used Cara’s measurements to find the height of the cone
let it be b so 2.5² + b² = 11.7², 6.25 + b² = 136.89², b²= 136.89 – 6.25 = 130.64, So b is equal to
sqaure root of 130.64, we get b = 11.42 rounding to the nearest hundredth is 11 cm. Therefore the height of the cone is about 11 centimeters.

Turn and Talk Cara has another ice cream cone. The radius and the height of the second cone is known. Explain how to use these dimensions to find the outside length of the cone.
Answer:
Outside length of the cone is square root of square of radius plus square of the height of the
second cone,

Explanation:
Given Cara has another ice cream cone. The radius and the height of the second cone is known.
Using these dimensions to find the outside length of the cone is sqaure root of square of radius plus square of the height of the second cone. Let the outside length of the cone be c and radius be a and the height of the second cone is b, So c = sqaure root of a² + b².

Check Understanding

Question 1.
Computer monitors are measured diagonally, from corner to corner. If the rectangular screen of a 40-inch monitor is 35 inches wide, what is the height of the monitor? Round to the nearest tenth.
$HMH Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem 8$
Answer:
The height of the monitor is 19 inches,

Explanation:
Given computer monitors are measured diagonally from corner to corner. If the rectangular screen of a 40-inch monitor is 35 inches wide, So let the height of the monitor is h, so applying Pythagorean theorem we have 35² + h² = 40², 1,225 + h² = 1,600, h²= 1,600 – 1,225 = 375, So h is equal to
sqaure root of 375, we get h = 19.36 rounding to the nearest tenth is 19 inches.

Question 2.
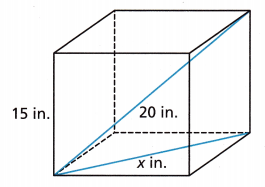
A 20-inch rod fits perfectly in a box 15 inches tall. What is the measurement of x in the diagram? Round to the nearest tenth.
$HMH Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem 9$
Answer:
The measurement of x in the diagram is 13 inches,

Explanation:
Given a 20-inch rod fits perfectly in a box 15 inches tall.
So the measurement of x in the diagram applying Pythagorean theorem we have
15² + x² = 20², 225 + x² = 400, x²= 400 – 225 = 175, So x is equal to sqaure root of 175,
we get x = 13.22 rounding to the nearest tenth is 13 inches.

On Your Own

Question 3.
Alexa can follow the sidewalk from the library to the school or she can travel across the grass directly.
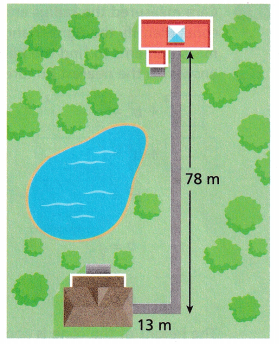
$HMH Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem 10$
A. Which route is longer?
Answer:
Longest route is the sidewalk from the library to the school,

Explanation:
The length of the sidewalk from the library to the school is78 m + 13 m = 91 m and
the length she can travel across the grass directly is let it be x, applying Pythagorean theorem
we have 13² + 78² = x², 169 + 6,084 = x², x²= 6,253 , So x is equal to
sqaure root of 6,253, we get x = 79.07 rounding to the nearest tenth is 79 m. as 91 m > 79 m so
the longest route is the sidewalk from the library to the school.

B. What is the difference between the lengths of the two routes?
Answer:
12 m,

Explanation:
As sidewalk from the library to the school distance is 91 m and the length she can travel across the grass directly is 79 m,
the difference between the lengths of the two routes is
91 m – 79 m = 12 m.

Question 4.
Adam’s closet measures 36 inches by 24 inches by 96 inches. What is the
longest distance between corners inside his closet? Round to the nearest tenth.
Answer:
The longest distance between corners inside his closet is 105 inches,

Explanation:
Given Adam’s closet measures 36 inches by 24 inches by 96 inches.
So the longest distance between corners inside his closet is square root of length² + width² + height²= sqaure root of 36² + 24² + 96²= sqaure root of 1,296 + 576 + 9,216 = sqaure root of 11,088 = 105.29 rounding to the nearest tenth is 105 inches.

Question 5.
The top of a building is a cone 10 meters tall with a radius of 4 meters at the base. What is the measurement of x in the diagram? Round to the nearest hundredth.
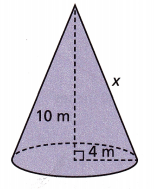
$HMH Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem 11$
Answer:
The measurement of x in the diagram is 11 m,

Explanation:
Given the top of a building is a cone 10 meters tall with a radius of 4 meters at the base. So the measurement of x in the diagram is applying Pythagorean theorem we have 10² + 4² = x²,
100 + 16 = x², x²= 116 , So x is equal to sqaure root of 116, we get x = 10.77 rounding
to the nearest tenth is 11 m.

Question 6.
Open-Ended Brianne purchased a box with a base diagonal length that is 45 centimeters long. What are two possible pairs of dimensions for the length and width of the box? Round to the nearest tenth.
Answer:
One pair: Length = 31.82 cm and Width = 31.82 cm,
Other pair: Length = 30 cm and Width = 33.54 cm,

Explanation:
Given Brianne purchased a box with a base diagonal length that is 45 centimeters long. The two possible pairs of dimensions for the length and width of the box are the base of the box has a
shape of a rectangle, and to find the length of the diagonal we can use the pythagoras theorem as follows: d² = l² + w²,Where d is the diagonal, l is the length and w is the width.
If we assume the base of the box to be a square, we can find one pair of dimension: as l = w,
d² = l² + l²= 2l², d² = 2 X 45 X 45 = 4,050, d is equal to square root of 4,050 is 63.63,
d² = 2l², l = 63.63/2 = 31.82 cm, So one pair is length = 31.82 cm and width = 31.82 cm,
To find other pair, we can just assume a value for the length,
so length = 30 cm then we can find the width as 45² = 30² + w², w²= 2,025 – 900 = 1,125,
w is eqaul to square root of 1,125 = 33.54 cm, So the other pair is
Length = 30 cm and Width = 33.54 cm.

For Problems 7-9, find the value for the unknown measurement in each rectangular prism or right cone. Round to the nearest tenth.

Question 7.
$HMH Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem 12$
Answer:
The unknown measurement is 29 in,

Explanation:
Given measurements as 24 in, 16 in and x in, applying Pythagorean theorem
we have 24² + 16² = x², 576 + 256 = x², x²= 832 , So x is equal to
sqaure root of 832, we get x = 28.84 rounding to the nearest tenth is 29 in.

Question 8.
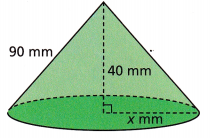
$HMH Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem 13$
Answer:
The unknown measurement is 81 mm,

Explanation:
Given measurements as 40 mm, x mm and 90 mm applying Pythagorean theorem
we have 40² + x² = 90², 1,600 + x²= 8,100, x²= 8,100 – 1,600 = 6,500 , So x is equal to
sqaure root of 6,500, we get x = 80.62 rounding to the nearest tenth is 81 mm.

Question 9.
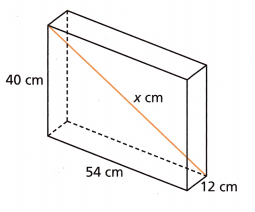
$HMH Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem 14$
Answer:
The unknown measurement is 68 cm,

Explanation:
Given measurements as 54 cm, 40 cm and x cm, First finding the hypotenuse side length of
54 cm, 12 cm and y cm, applying Pythagorean theorem we have 54² + 12² = y²,
2,916 + 144 = y², y²= 3,060, So y is equal to sqaure root of 3,060, we get y = 55.31 rounding
to the nearest tenth is 55 cm. Now we have 55 cm, 40 cm and x cm, applying Pythagorean theorem
we have 55² + 40² = x², 3,025 + 1,600 = x², x²= 4,625, So x is equal to
sqaure root of 4,625, we get x = 68.0073 rounding to the nearest tenth is 68 cm.

Question 10.
Use Structure The Maron Luggage Company claims they have a suitcase large enough to fit a 34-inch baseball bat inside. If the suitcase has height and depth 17 inches by 11 inches, what must its whole-number length be, at minimum?
Answer:
Its whole- number length will be 34 inches,

Explanation:
Given the Maron Luggage Company claims they have a suitcase large enough to fit a 34-inch baseball bat inside. If the suitcase has height and depth 17 inches by 11 inches, Its whole-number length will be 34 inch only aslength will be the same, therefore it is 34 inches.

Question 11.
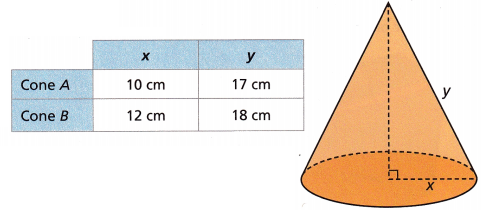
A. Which is taller, Cone A or Cone B?
$HMH Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem 15$
Answer:
Cone A,

Explanation:
Given cone A – x as 10 cm, y as 17 cm, let z be the height applying Pythagorean theorem
we have 10² + z² = 17², 100 + z²= 28, z²= 289 – 100 = 189, So z is equal to
sqaure root of 189, we get z = 13.74 cm rounding to the nearest tenth is 14 cm,
given cone B – x as 12 cm, y as 18 cm, let z be the htpotenuse,
applying Pythagorean theorem we have 12² + z² = 18²,
144 + z²= 324, z²= 324 – 144 = 180, So z is equal to sqaure root of 180, we get z = 13.41 cm rounding to the nearest tenth is 13 cm, upon compairing the heights of Cone A and Cone B , cone A > cone B as 14 cm > 13 cm, therefore cone A is taller than cone B.

B. By how much? Round to the nearest hundredth.
Answer:
Almost 1 cm,

Explanation:
Cone A has height 13.74 cm and cone B has 13.41 cm, So much taller is 13.74 cm – 13.41 = 0.33 cm,
nearly 1 cm tall.

Question 12.
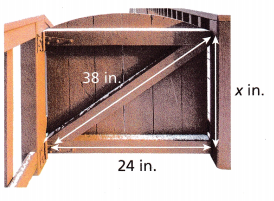
Find the value of x in the diagram to the nearest tenth.
$HMH Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem 16$
Answer:
The value of x in the diagram is 29 in,

Explanation:
Given 24 in and 38 in and x in applying Pythagorean theorem
we have 24² + x² = 38², 576 + x² =1,444, x²= 1,444 – 576 = 868, So x is equal to
sqaure root of 868, we get x = 29.46 in rounding to the nearest tenth is 29 in. Therefore the value of x
in the diagram is 29 in.

Question 13.
Reason What is the length of the longest rod that can fit inside this cube? Round to the nearest tenth, and show your work.
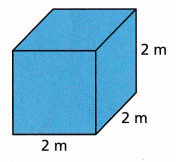
$HMH Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem 17$
Answer:
The length of the longest rod that can fit inside this cube is 4 m,

Explanation:
Asking to find the length of the longest rod that can fit inside this cube is
Length of a cube(l) = 2 m, Breadth of a cube(b) = 2 m, Height of a cube(h) = 2m,
The length of the longest rod is the diagonal of the cube.
So, We have to find the diagonal of the cube as Diagonal of a cube = √ 3 X side
Diagonal of a cube = 1.732 X 2, Diagonal of a cube = 3.46 ≈ 4 m. So the length of the
longest rod that can fit inside this cube is 4 m.

Lesson 11.3 More Practice/Homework

Question 1.
Geography The distances between Centerville, Springfield, and Capital City form a right triangle. The distance between Centerville and Springfield is 913 kilometers and the distance between Springfield and Capital City is 976 kilometers.
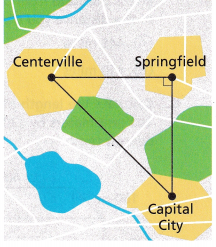
$HMH Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem 18$
A. What is the direct distance between Centerville and Capital City? Round to the nearest kilometer.
Answer:
The direct distance between Centerville and Capital CityExplanation is 1,336 kilometers,

Explanation:
Given geography the distances between Centerville, Springfield, and Capital City form a right triangle.
The distance between Centerville and Springfield is 913 kilometers and the distance between Springfield and Capital City is 976 kilometers. Let x be the direct distance between Centerville and Capital City applying Pythagorean theorem we have 913² + 976² = x²,
833,569 + 952,576 = x², x²= 17,86,145, So x is equal to sqaure root of 17,86,145, we get x = 1,336.46 rounding to the nearest tenth is 1,336 kilometers.

B. Anwell travels from Centerville to Springfield, then on to Capital City. Yue travels directly from Centerville to Capital City. How much farther does Anwell travel than Yue? Round to the nearest kilometer.
Answer:
553 kilometers,

Explanation:
Given Anwell travels from Centerville to Springfield, then on to Capital City. Yue travels directly from
Centerville to Capital City. Centerville to Springfield then on to Capital City 913 kilometers + 976 kilometers = 1,889 kilometers, Yue travels directly from Centerville to Capital City is
1,336 kilometers, Anwell travel than Yue is 1,889 kilometers – 1,336 kilometers = 553 kilometers.

Question 2.
Attend to Precision Find the radius of this ice cup. Round to the nearest tenth.
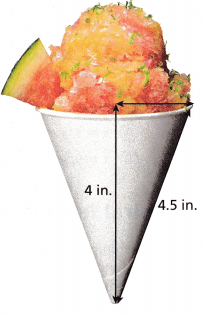
$HMH Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem 19$
Answer:
The radius of this ice cup is 2 in,

Explanation:
Given the lengths of ice cup as height 4 in hypotenuse 4.5 in, let r be the radius of ice cup,
applying Pythagorean theorem we have 4² + r² = 4.5², 16 + r²= 20.25, r²= 20.25 – 16, So x is equal to
sqaure root of 4.25, we get r = 2.06 rounding to the nearest tenth is 2 in.

Question 3.
Math on the Spot A child has an empty box that measures 4 inches by 6 inches by 3 inches. What is the length of the longest pencil that will fit into the box, given that the length of the pencil must be a whole number of inches? Do not round until your final answer.
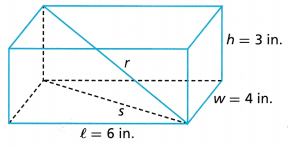
$HMH Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem 20$
Answer:
The longest pencil that will fit into the box is 8 inches,

Explanation:
Given a child has an empty box that measures 4 inches by 6 inches by 3 inches.
The length of the longest pencil that will fit into the box is the diagonal of cuboid, which is $= \sqrt l 2 + b 2 + h 2,$ $∴$ Diagonal of box $= \sqrt 4 2 + 6 2 + 3 2,$ gest pencil that will fit into the box is 8 inches.

Question 4.
Mr. Johnston supports a young tree by using a stake and a string forming a right angle with the ground. What is the length of the string? Round to the nearest tenth.
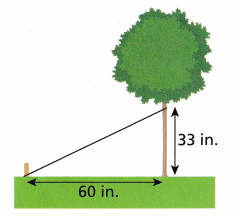
$HMH Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem 21$
Answer:
The length of the string is 68 in,

Explanation:
Given Mr. Johnston supports a young tree by using a stake and a string forming a right angle with the ground. Let l be the length of the string applying Pythagorean theorem
we have 60² + 33² = l², 3,600 + 1,089 = l², l²= 4,689, So l is equal to sqaure root of 4,689, we get l = 68.47 rounding to the nearest tenth is 68 in.

Test Prep

Question 5.
The state of Wyoming is almost rectangular, with an approximate width of 365 miles and an approximate height of 276 miles. If you fly across the state from opposite corners, what is the best approximation of the distance you travel?
(A) 448 miles
(B) 450 miles
(C) 458 miles
(D) 462 miles
Answer:
(C) 458 miles,

Explanation:
Given the state of Wyoming is almost rectangular with an approximate width of 365 miles and an approximate height of 276 miles. If we fly across the state from opposite corners, the best approximation of the distance I travel is let it be d applying Pythagorean theorem
we have 365² + 276² = d², 132,225 + 76,176 = d², d²= 209,401, So d is equal to
sqaure root of 209,401 we get d = 457.60 rounding to the nearest tenth is 458 miles which matches with bit (C).

Question 6.
Calculate the length of the longest rod that can fit in a box measuring 100 centimeters by 130 centimeters by 400 centimeters. Round to the nearest tenth.
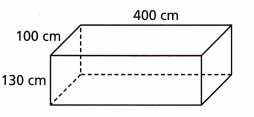
$HMH Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem 22$
____________ centimeters
Answer:
The length of the longest rod that can fit in a box is 432 centimeters,

Explanation:
Given a box measuring 100 centimeters by 130 centimeters by 400 centimeters
The length of the longest rod that will fit into the box is the diagonal of cuboid, which is $= \sqrt l 2 + b 2 + h 2,$ $∴$ Diagonal of box $= \sqrt 100 2 + 130 2 + 400 2,$ $∴$ Diagonal of box $= \sqrt186,900= 432.31 on rounding it is 432 centimeters,$ therefore the longest rod that will fit into the box is 432 centimeters.

Question 7.
Which set of measurements could possibly fit the given cone diagram?
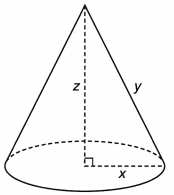
$HMH Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem 23$
(A) x = 3, y = 4, z = 5
(B) x = 9, y = 6, z = 10
(C) x = 3, y = 8, z = 5
(D) x = 6, y = 10, z = 8
Answer:
(A) x = 3, y = 4, z = 5,

Explanation:
The measurements that could possibly fit the given cone diagram as it is a right traingle we
applying Pythagorean theorem and checking with bits as Bit (A) x = 3, y = 4, z = 5,
3² + 4² = 5², 9 + 16 = 25as 25 = 25 matches, checking with bit (B) x = 9, y = 6, z = 10,
9² + 6² = 81 + 36 = 117 ≠ 10²≠ 100, So not form a right triangle,
Checking with bit (C) x = 3, y = 8, z = 5, 3² + 8² = 9 + 64 = 73 ≠ 5²≠ 25,
So not form a right triangle, Checking with bit (D) x = 6, y = 10, z = 8,
6² + 10² = 36 + 100 = 136 ≠
8²≠ 64,
So not form a right triangle, Therfore only
bit (A) x = 3, y = 4, z = 5 measurements that could possibly fit.

Spiral Review

Question 8.
A fun park charges $10 for admission and then $2 for every ride. Write a function that determines the amount of money spent, y, based on the number of rides ridden, x.
Answer:
y = 2x + 10,

Explanation:
Given a park charges $10 for admission and then $2 for every ride. The function that determines
the amount of money spent y based on the number of rides ridden x is y= 2x + 10.

Question 9.
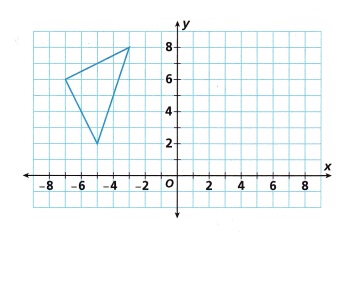
Reflect the triangle across the y-axis and draw the image.
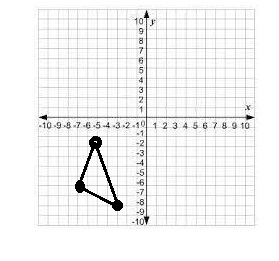
$Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem-5$

Answer:

$Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem-6$

Explanation:
Reflected the triangle across the y-axis and drawn the image as shown above, Given A(-5,2), B(-7,6) and C(-3,8) so we get A(-5,-2), B(-7,-6) and C(-3,-8).

HMH Into Math Grade 8 Module 11 Lesson 3 Answer Key Apply the Pythagorean Theorem

Leave a Comment Cancel Reply