Into Math Grade 8 Module 10 Review Answer Key

We included HMH Into Math Grade 8 Answer Key PDF Module 10 Review to make students experts in learning maths.

HMH Into Math Grade 8 Module 10 Review Answer Key

Vocabulary

For Problems 1-4, give two examples of each type of number.

Question 1.
rational number
Answer:
\(\frac{1}{2}\), \(\frac{3}{5}\),

Explanation:
A rational number is a number that is expressed as the ratio of two integers, where the denominator should not be equal to zero or A rational number is a number that can be expressed as the quotient or fraction p/q of two integers, a numerator p and a non-zero denominator q.
Examples:  \(\frac{1}{2}\), \(\frac{3}{5}\).

Question 2.
irrational number
Answer:
√2, √3, √5, √11, √21, π(Pi) are all irrational,

Explanation:
Numbers cannot be written as a ratio of two integers, Irrational numbers are numbers that cannot be expressed as the ratio of two whole numbers. √2, √3, √5, √11, √21, π(Pi) are all irrational.

Question 3.
terminating decimal
Answer:
2.675 –  Since there are 3 digits after the decimal point it is a terminating decimal number.
23.5 is a terminating decimal number because it has 1 digit after the decimal point,

Explanation:
A decimal which can be expressed in a finite number of figures or for which all figures to the right of some place are zero. 2.675 –  Since there are 3 digits after the decimal point,
it is a terminating decimal number. 23.5 is a terminating decimal number because it has
1 digit after the decimal point.

Question 4.
repeating decimal
Answer:
Repeating Decimals: (13 / 3) = 4.333, (4 / 11) = . 363636,

Explanation:
A repeating decimal or recurring decimal is decimal representation of a number whose digits are periodic and the infinitely repeated portion is not zero. It can be shown that a number is rational if and only if its decimal representation is repeating or terminating. Examples: (13 / 3) = 4.333, (4 / 11) = . 363636.

Question 5.
Explain how the terms perfect square and square root are related.
Answer:
Both are squaring only,
The process of multiplying a number times itself is called squaring. Numbers whose square roots are
whole numbers, (or more accurately positive integers) are called perfect square numbers.
Numbers with decimals aren’t perfect square roots.
Perfect square are sqaure roots only but all sqaure roots are not perfect sqaures,

Explanation:
The process of multiplying a number times itself is called squaring. Numbers whose square roots are
whole numbers, (or more accurately positive integers) are called perfect square numbers.
Numbers with decimals aren’t perfect square roots.
Perfect square: A perfect square is a number that can be expressed as the product of an integer by itself or as the second exponent of an integer, Sqaure root: The square root of a number is the factor
that we can multiply by itself to get that number.

Concepts and Skills

Question 6.
Select all numbers that are irrational.
(A) –\(\frac{5}{12}\)
(B) \(\frac{\pi}{2}\)
(C) \(0 . \overline{15}\)
(D) \(\sqrt{5}\)
(E) \(\frac{1}{6}\)
(F) \(\sqrt{25}\)
Answer:
(A) –\(\frac{5}{12}\),
(B) \(\frac{\pi}{2}\),
(C) \(0 . \overline{15}\),
(D) \(\sqrt{5}\),
(E) \(\frac{1}{6}\),
Bits A, B, C, D, and E are irrational,

Explanation:
Checking all numbers that are irrational, Bit (A) –\(\frac{5}{12}\) = -0.4166666,
repeating so irrational, Bit (B) \(\frac{\pi}{2}\) = 1.571428 repeating so irrational,
Bit (C) \(0 . \overline{15}\)= 0.151515, repeating so irrational,
Bit (D) \(\sqrt{5}\)= 2.23606 repeating so irrational,
Bit (E) \(\frac{1}{6}\) = 0.166666 repeating so irrational,
Bit (F) \(\sqrt{25}\) = 5 not repeating so not irrational, Bits A, B, C, D, and E are irrational.

Question 7.
Determine whether each number is rational or irrational.

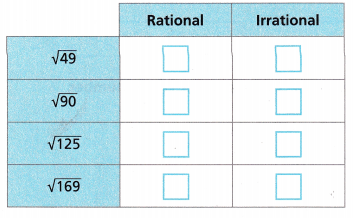
Answer:

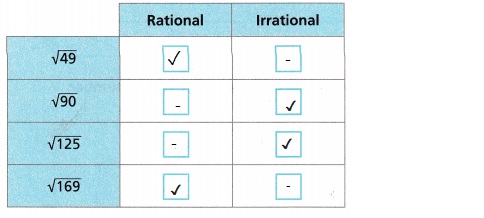
Explanation:
Given to determine whether each number is rational or irrational.
49 is a perfect square number which can be obtained by a square of 7 and it is also a composite number. Hence, the square root of 49 is a rational number. The square root of 90 is evaluated in the decimal form as 9.486. Hence, it is irrational. √125 is an irrational number, since the simplification of
√125 will produce a non-terminating value. 169 is a perfect square number which can be
obtained by a square of 13 Hence, the square root of 49 is a rational number.

Question 8.
Use Tools Write a fraction equivalent to 0.24? State what strategy and tool you will use to answer the question, explain your choice, and then find the answer.
Answer:
\(\frac{6}{25}\) Removing decimal point Finding common factor and cancel,

Explanation:
Step 1: Remove decimal point. To remove decimal point, place 100 in the denominator,
\(\frac{24}{100}\), Step 2: Find the common factor in both numbers,
\(\frac{24}{100}\) = \(\frac{4 X 6}{4 X 25}\), Step 3: Cancel 4 from both we get
\(\frac{6}{25}\). Strategy and tool I have used to answer the question is
Removing decimal point finding common factor and cancel common factors we get results.

For Problems 9-10, write each repeating decimal as a fraction.

Question 9.
\(0 . \overline{18}\)
Answer:
\(\frac{2}{11}\),

Explanation:
Let x = 0.18 Since $x$ is recurring in 2 decimal places, we multiply it by 100,
100x = 18.18, 100x – x = 18.18 – 0.18, 99x = 18, we divide both sides by 99 we get
x = \(\frac{18}{99}\), x = \(\frac{2}{11}\).

Question 10.
\(0 . 3\overline{6}\)
Answer:
\(\frac{11}{30}\),

Explanation:
$\text{We require to establish 2 equations with the repeating}$$\text{number after the decimal point,}$Let x = \(0 . 3\overline{6}\), 10 x = \(3.\overline{6}\) – equation 1,
100 x = \(36.\overline{6}\) – equation 2, Subtract (1) from (2) to elminate repeated value
(100x – 10x) = (\(36.\overline{6}\) – \(3.\overline{6}\)),
90x = 33, x = \(\frac{33}{90}\) = \(\frac{11}{30}\).

Question 11.
Do you see a pattern in the number 0.31311311131111…? Is it rational or irrational? Explain your reasoning.
Answer:
Irrational,

Explanation:
Given pattern in the 0.31311311131111… is irrational as it is in the decimal form and
non-terminating value.

For Problems 12-13, find all solutions of the equation.

Question 12.
x³ = 11
x = ___________
Answer:
x =2.2239,

Explanation:

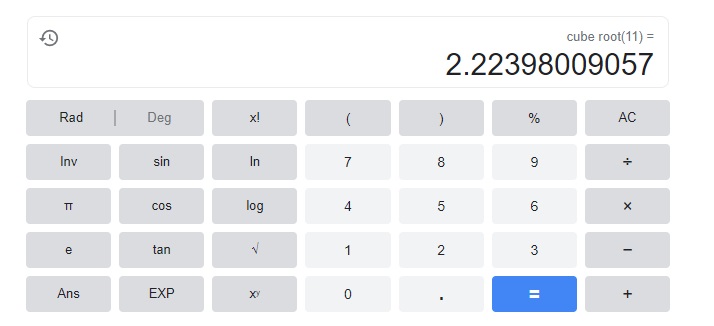
The cube root of x is 2.2239.

Question 13.
n² = 0.16
n = ___________
Answer:
n = 0.4,

Explanation:

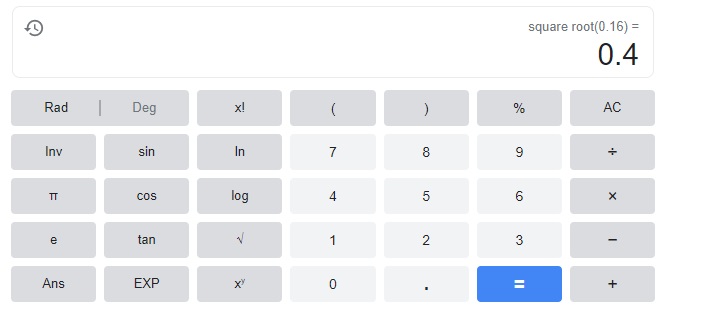
The sqaure root of n is 0.4.

Question 14.
A cube has a volume of 216 cubic inches. What is the edge length of the cube?
(A) 6 inches
(B) 15 inches
(C) 18 inches
(D) 36 inches
Answer:
(A) 6 inches,

Explanation:
Given a cube has a volume of 216 cubic inches. The volume of cube is cuberoot of edge,
So the edge length of the cube is cuberoot of 216 cubic inches,

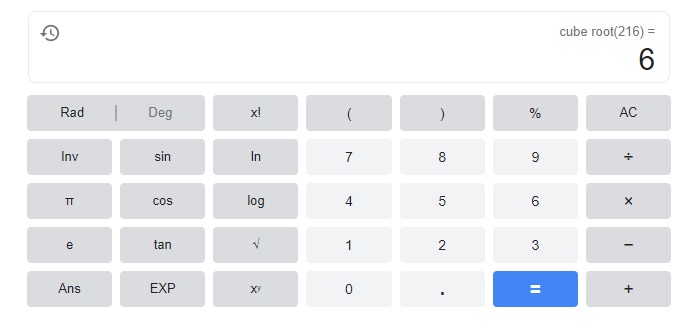
Matches with bit (A) 6 inches.

Question 15.
Explain why the equation x² = 64 has two solutions, but the equation x³ = 64 has only one solution.
Answer:
x = 8, x = -8,
A quadratic expression can be written as the product of two linear factors and each factor
can be equated to zero, So there exist two solution.
A quadratic equation has one solution when the discriminant is zero so the equation x³ = 64
has only one solution,

Explanation:
A quadratic expression can be written as the product of two linear factors and each factor
can be equated to zero, So there exist two solution.
x²- 64 = 0, x²-8² = 0, (x+8)(x-8) = 0, Since a²- b² = (a+b)(a-b),
Since the product is 0, Either x + 8 = 0, x = -8 or x – 8 = 0, x = 8.
A quadratic equation has one solution when the discriminant is zero so the equation x³ = 64
has only one solution, The value of discriminant b² – 4ac is zero.
For example, x² + 2x + 1 = 0 has only one solution x = -1.
Discriminant = b² – 4ac = 2² – 4 (1) (1) = 0, So Factorization is : (x – 4)  •  (x² + 4x + 16) .

For Problems 16-18, estimate the value of the root to the nearest whole number.

Question 16.
\(\sqrt{53}\) ____________
Answer:
7,

Explanation:

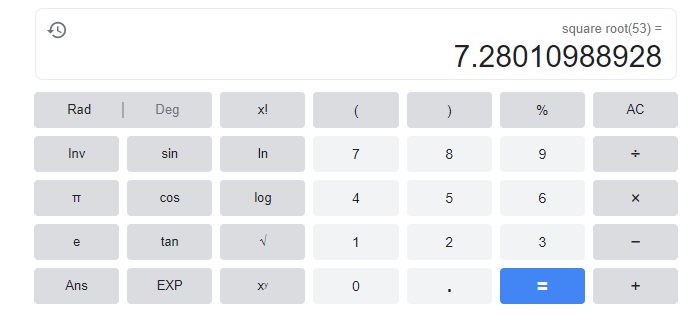
The value of the root to the nearest whole number is 7.

Question 17.
\(\sqrt[3]{118}\) _____________
Answer:
5,

Explanation:

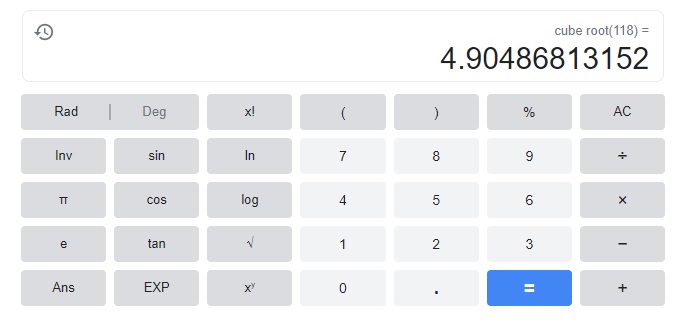
The value of the root to the nearest whole number is 5.

Question 18.
Select all values that are greater than 4.
(A) \(\sqrt[3]{8}\)
(B) \(\sqrt{9}\)
(C) \(\sqrt{10}\)
(D) \(\sqrt[3]{12}+2\)
(E) \(\sqrt{27}\)
(F) 2 π
Answer:
(E) \(\sqrt{27}\) and (F) 2 π,

Explanation:
Checking all values that are greater than 4, Bit (A) \(\sqrt[3]{8}\) = 2.8284 which will not match, bit (B) \(\sqrt{9}\) = 3 which will not match, bit (C) \(\sqrt{10}\) = 3.1622 which will not match, bit (D) \(\sqrt[3]{12}+2\) = 2.25 which will not match,
bit (E) \(\sqrt{27}\) = 5.196 which matches, bit (F) 2 π = 2 X 3.14 = 6.28 which matches therefore bits (E) \(\sqrt{27}\) and (F) 2 π matches and values are greater than 4.

For Problems 19-20, plot the set of numbers at their approximate locations on the number line.

Question 19.

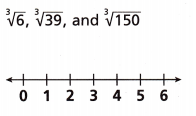
Answer:

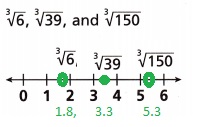
Explanation:
Given to plot the set of numbers at their approximate locations on the number line so
cube root of 6 is 1.817, cube root of 39 is 3.391, cube root of 150 is 5.313 plotted as shown above.

Question 20.

Answer:

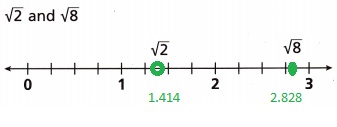
Explanation:
Given to plot the set of numbers at their approximate locations on the number line so
Sqaure root of 2 is 1.414, Square root of 8 is 2.828 plotted as shown above.