Into Math Grade 8 Module 10 Lesson 1 Answer Key Understand Rational and Irrational Numbers

We included HMH Into Math Grade 8 Answer Key PDF Module 10 Lesson 1 Understand Rational and Irrational Numbers to make students experts in learning maths.

HMH Into Math Grade 8 Module 10 Lesson 1 Answer Key Understand Rational and Irrational Numbers

I Can determine whether a number is rational and write a given rational number as a fraction.

Spark Your Learning

In softball, a player’s batting average ¡s the number of hits divided by the number of at-bats. Write each player’s batting average as a decimal. What do you notice?

Answer:
Jamilla = 0.4, Callie = 0.125, Mayumi = 0.44444, Elena = 0.373737, Kaycee = 0.1944,

Explanation:
Given in a softball, a player’s batting average is the number of hits divided by the number of at-bats. Wrote each player’s batting average as a decimal as Jamilla = 0.4, Callie = 0.125,
Mayumi = 0.44444, Elena = 0.373737, Kaycee = 0.1944, I notice Mayumi is having greatest batting average.

Turn and Talk Do you think all fractions have decimal representations that either end or have digits that repeat? Try some additional fractions and discuss your conjecture.
Answer:
Yes,

Explanation:
Yes, I think all fractions have decimal representations that either end or have digits that repeat,
If the prime factorization of the denominator contains all 2’s, all 5’s, or a combination of 2’s and 5’s only, then the decimal expansion of the fraction will be terminating,
also if the denominator is a power of ten to begin with, we don’t have to factor, the decimal expansion will be terminating, For example, 3/10=0.3, 37/100=0.37, 528/1000=0.528, 345/10,000=0.0345 and so on, let’s look at other examples:
1/2=0.5 because the denominator is 2, 3/4=0.75 because 4 = 2×2,
2/5=0.4 because the denominator is 5.
If the denominator is a prime number other than a 2 or a 5 or if the prime factorization of the denominator contains anyprime numbers other than 2’s or 5’s, the decimal expansion of
the fraction will be repeatin, let’s look at some examples: 2/3=0.666…(the prime number 3 makes the decimal repeat), 5/6=0.8333…(6=2×3) 4/7=0.571428571428571428571428…(prime number 7).

Build Understanding

A rational number is any number that can be written as a ratio in the form \(\frac{a}{b}\), where a and b are integers and b is not 0. Every rational number can be written as a terminating decimal or a repeating decimal. Examples of rational numbers are:
\(\frac{3}{8}\) = 0.375; 7 = \(\frac{7}{1}\), 0.2 = \(\frac{1}{5}\); 0.11111…= \(\frac{1}{9}\).

Connect to Vocabulary
An irrational number is a number that cannot be written in the form \(\frac{a}{b}\), where a and b are integers and b is not 0.

Question 1.
Is every number rational?

A. Consider the decimal 1.345345634567….
Does the decimal appear to have a repeating pattern? Explain.
____________________
Do you think 1.345345634567… is a rational number? Why or why not?
Answer:
Yes repeating pattern, Yes, 1.345345634567… is a rational number,

Explanation:
Considering the decimal 1.345345634567….
Yes, the decimal appear to have a repeating pattern as the numbers after the decimal keep going on and on. Yes, I think 1.345345634567… is a rational number because every positive number is a rational number.

B. You have learned that pi (π) is the ratio of the circumference of any circle to its diameter. The decimal value of pi is shown below.
π = 3.145926535897932……..
Pi is an irrational number, but it can be written as a ratio. How can this be?
__________________________
There are two ways to write a repeating decimal. You can use an ellipsis (three dots) to show that the repeating pattern continues:
0.111… ,0.235235235…, and 0,244414444…
Or, you can write an overbar over the part of the decimal that repeats:
\(0 . \overline{1}\), \(0 . \overline{235}\), and \(0.2 \overline{4}\)
Answer:
Yes, Pi is an irrational number, but it can be written as a ratio,

Explanation:
As a ratio can be expressed as a:b, regardless of [ir]rational nature of
a or b, or both. Hence, ratios involving pi or any other irrational quantities can be mani-pulated like any other ratios.
Now, when you divide a rational number by another rational number, you get a rational number.

Turn and Talk Convert \(\frac{1}{36}\) to a decimal. Write the decimal using an ellipsis and using an overbar. Explain the process you used.
Answer:
0.0277…. and \(0 . 02\overline{7}\),

Explanation:
Given to convert \(\frac{1}{36}\) to a decimal using an ellipsis as we have \(\frac{1}{36}\) = 0.027777777, as ellipsis is three dots to show repeating pattern continues, as we have 7 is repeating so it is 0.02777…. and wrote overbar for 7 as repeating \(0 . 02\overline{7}\).

Question 2.
A basketball player’s free throw percentage is 82.5%, or 0.825. Write this as a fraction.

A. Identify the place value of the last digit in the terminating decimal. Use this to determine the denominator of the fraction. The digits to the right of the decimal point are the numerator of the fraction.

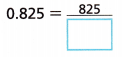
Answer:
0.825 = \(\frac{825}{1000}\),

Explanation:
Identifying the place value of the last digit in the terminating decimal as thousandth,
Using this to determine the denominator of the fraction as 1000 and the digits to the right of the
decimal point 825 are the numerator of the fraction therefore 0.825 = \(\frac{825}{1000}\).

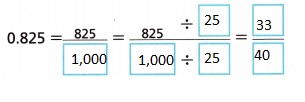
B. Write the fraction in lowest terms. Identify the greatest common factor (GCF) of the numerator and denominator. Divide the numerator and denominator by the GCF.

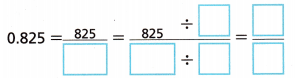
Answer:

Explanation:
To write the fraction \(\frac{825}{1000}\) in lowest terms,
we identify the greatest common factor (GCF) of the numerator and denominator as the prime factorization of 825, 825 = 3 × 5 × 5 × 11, the prime factorization of 1000,
1000 = 2 × 2 × 2 × 5 × 5 × 5 finding the GCF, multiplying all the prime factors common to both numbers: therefore, GCF = 5 × 5 =25. Now dividing the numerator and denominator by the GCF as \(\frac{825}{1000}\) ÷ \(\frac{25}{25}\) = \(\frac{33}{40}\).

Question 3.
You can also convert a repeating decimal to a fraction. A. Write \(0 . \overline{5}\) as a fraction. Let x be the given decimal.

Answer:
x = \(\frac{5}{9}\),

Explanation:
To write \(0 . \overline{5}\) as a fraction. Let x be the given decimal so x = 0.555555…

we get x = \(\frac{5}{9}\).

B. Write \(0 . \overline{18}\) as a fraction.
Let x be the given decimal.
Write the first few repeating digits.
x = 0.1818……….
Multiply both sides of the equation by 100 so that the repeating digits appear just to the left of the decimal point.
Subtract an expression equal to x from both sides.

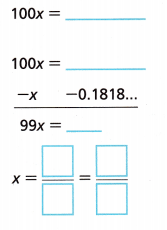
Solve for x. Then simplify the fraction.
Answer:
x = \(\frac{99}{18}\) or \(\frac{11}{2}\),

Explanation:
To write \(0 . \overline{18}\) as a fraction.
Let x be the given decimal. Writing the first few repeating digits.
x = 0.1818……….Multiplying both sides of the equation by 100 so that the repeating digits appear just to the left of the decimal point.
Subtract an expression equal to x from both sides as

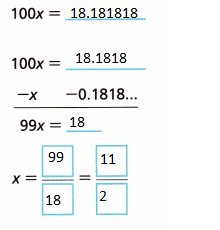
x = \(\frac{99}{18}\) or \(\frac{11}{2}\).

Question 4.
The average number of goals scored per game for a soccer team is shown. Write this rational number as a fraction or mixed number.

Identify the repeating digit(s) of the decimal. ____________
Let x be the given decimal. Write an equation with the decimal. x = 1.62333….
Multiply by a power of 10 so that the first repeating digit appears just to the right of the decimal point.
Multiply both sides of the equation by 100. 100x = 162.333….. Multiply by a power of 10 so that the first repeating digit appears just to the left of the decimal point. Multiply both sides of the equation by 1000.
Subtract the expression equal to from both sides.

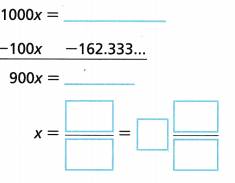
Solve for x. Write the fraction as a mixed number and simplify.
Answer:

Explanation:
Given the average number of goals scored per game for a soccer team is shown. Wrote this rational number as a fraction or mixed number, Let x be the given decimal.
Writing an equation with the decimal. x = 1.62333…. Multiply by a power of 10 so that the first repeating digit appears just to the right of the decimal point.
Multiply both sides of the equation by 100. 100x = 162.333…..
Multiply by a power of 10 so that the first repeating digit appears just to the left of the decimal point.
Multiply both sides of the equation by 1000.
we get 1623.33, Subtract the expression equal to from both sides. 1000x = 1623.33
-100x = -162.33
900x = 1,460.997
x = \(\frac{1460}{900}\) or 1\(\frac{561}{900}\).

Check Understanding

Question 1.
Convert \(\frac{1}{18}\) to a decimal.
A. Write the decimal using an ellipsis.
Answer:
0.0555…,

Explanation:
Given to convert \(\frac{1}{18}\) to a decimal using an ellipsis as we have \(\frac{1}{18}\) = 0.05555555 as ellipsis is three dots to show repeating pattern continues,
as we have 5 is repeating so it is 0.0555….

B. Write the decimal using an overbar.
Answer:
\(0 . 0\overline{5}\),

Explanation:
Given to convert \(\frac{1}{18}\) as we have \(\frac{1}{18}\) = 0.05555
and write overbar for 5 as repeating \(0 . 0\overline{5}\).

Question 2.
Use your calculator to find the decimal equivalent of \(\sqrt{17}\). Do you think this is a rational number? Why or why not?
Answer:
No not rational,
\(\sqrt{17}\) is an irrational number,

Explanation:
$\sqrt{17}$ is irrational essentially as a consequence of $17$ being prime :- that is having no positive factors apart from $1$ and itself. Here’s a sketch of a proof: Suppose $\sqrt{17}=\frac{p}{q}$ for some integers $p$, $q$, with $q\ne 0$.
Without loss of generality, $p,q>0$ and $p$ and $q$ have no common factor greater than $1$.
If they did have a common factor, then you could divide both by that common factor to get a smaller $p_1$ and $q_1$ with $\sqrt{17}=\frac{p_1}{q_1}$, Then ${\mathrm{p2}}^{}=17{\mathrm{q2}}^{}$ and since ${\mathrm{p2}}^{}$ is a multiple of $17$ and
$17$ is prime, $p$ must be a multiple of $17$.
Let $k=\frac{\mathrm{p/}}{\mathrm{17,}}$Then $17{\mathrm{q2}}^{}={\mathrm{p2}}^{}={(17k)2}^{}=17\cdot 17k^{\mathrm{2,}}$Divide both ends by $17$ to find:
${\mathrm{q2}}^{}=17{\mathrm{k2}}^{}$ hence $q$ is a multiple of $17$. So both $p$ and $q$ are divisible by $17$,
contradicting our assumption that $p$ and $q$have no common factor greater than $1$.
So there is no such pair of integers $p$ and $q$.

For Problems 3-5. write the rational number as a simplified fraction or as a mixed number in simplest form.

Question 3.
1.905
Answer:
\(\frac{381}{200}\) or 1\(\frac{181}{200}\),

Explanation:
To convert the decimal 1.905 to a fraction, just follow these steps:
Step 1: Write down the number as a fraction of one:
1.905 = 1.9051,
Step 2: Multiply both top and bottom by 10 for every number after the decimal point:
As we have 3 numbers after the decimal point,
we multiply both numerator and denominator by 1000.
So, 1.9051 = (1.905 × 1000)(1 × 1000) = 19051000.
Step 3: Simplify (or reduce) the above fraction by dividing both numerator and denominator by the GCD( Greatest Common Divisor) between them. In this case, GCD(1905,1000) = 5.
So, (1905÷5)(1000÷5) = 381200 when reduced to the simplest form.
As the numerator is greater than the denominator, we have an improper fraction, so we can also express it as a mixed number, thus \(\frac{381}{200}\) or
1\(\frac{181}{200}\),when expressed as a mixed number.

Question 4.
0.828282…
Answer:
\(\frac{82}{99}\),

Explanation:
Given 0.828282… to convert to fraction, so

Question 5.
\(0.4 \overline{3}\)
Answer:
\(\frac{13}{30}\),

Explanation:
Given \(0.4 \overline{3}\) to convert to fraction, so

On Your Own

Question 6.
The diagram shows the number of instruments in the string section of an orchestra. There are 7 cellos, 4 double bases, and 11 each of first violins, second violins, and violas.

A. Use ratio notation and decimal notation to describe the relationship between the number of double basses and the total number of instruments in the string section.
Answer:
Ratio notation: 4:44,
Decimal notation: \(0.\overline{09}\),

Explanation:
Given the diagram shows the number of instruments in the string section of an orchestra. There are 7 cellos, 4 double basses, and 11 each of first violins, second violins, and violas. So using ratio notation and decimal notation to describe the relationship between the number of double basses and the total number of instruments in the string section. As a ratio is written with a colon between
the two quantities that are being compared as we have double basses 4 and total number are
7 + 4 + 11 + 11 + 11 = 44, So Ratio notation: 4 : 44 and as decimal notation is the representation of a fraction using the base 10 along with a decimal point we have \(\frac{4}{44}\) = \(\frac{1}{11}\) = 0.09090909…. so it is \(0.\overline{09}\).

B. Is the relationship in Part A rational or irrational? Give two different justifications for your answer.
Answer:
Yes, rational,

Explanation:
Relationship is rational Justifications: 1. As we know rational numbers are one very common type of number that we usually study after integers in math. These numbers are in the form of p/q, where p and q can be any integer and q ≠ 0 and
The word “Rational” is originated from the word “ratio”.
So, rational numbers are very well related to the ratio concept of ratio.
As the relationship in part A is ratio notation: 4: 44 or \(\frac{4}{44}\) = \(\frac{1}{11}\) it is rational, 2. As we know non-terminating decimals with repeating patterns of decimals are also rational numbers and we have relationship in part A as \(0.\overline{09}\) a non terminating decimals therefore the relationship is rational.

Question 7.
The ratio of 8th graders in a chess club to the total number of members is \(0 . \overline{45}\). Write the decimal as a fraction. Show your work.

Answer:
\(\frac{45}{99}\) or \(\frac{5}{11}\),

Explanation:
Given the ratio of 8th graders in a chess club to the total number of members is \(0 . \overline{45}\). Writing the decimal as a fraction

Question 8.
Critique Reasoning A student claimed that the number -4 is not rational because it is not a ratio of two integers. Do you agree or disagree? Explain.
Answer:
Disagree,

Explanation:
Given a student claimed that the number -4 is not rational because it is not a ratio of two integers. I disagree because as it the ratio of two integers of -4 and 1.

Question 9.
Use Repeated Reasoning Pi (π) is an irrational number. What can you say about the numbers \(\frac{\pi}{2}\), \(\frac{\pi}{3}\), \(\frac{\pi}{4}\)and so on? Are these rational or irrational?
Answer:
The numbers \(\frac{\pi}{2}\), \(\frac{\pi}{3}\), \(\frac{\pi}{4}\) and so on are irrational only,

Explanation:
The number pi(π) is a mathematical constant representing the ratio of a circle’s circumstance to its diameter. It’s an irrational number, meaning that it can’t be represented by a common fraction.
We can’t write it down as a non-infinite decimal and is a non-terminating, non-repeating decimal number.
Hence the numbers such as \(\frac{\pi}{2}\), \(\frac{\pi}{3}\), \(\frac{\pi}{4}\) and so on are also irrational only as they are multipled by pi(π) the resulting numbers are also
non-terminating, non-repeating decimal number.

Question 10.
STEM The atomic weight of an element is the total mass of the protons, neutrons, and electrons. The ratio of the mass of the protons in radon to the atomic mass of radon is 0.387387387… . Write the decimal as a fraction.

Answer:
\(\frac{43}{111}\),

Explanation:
Given the ratio of the mass of the protons in radon to the atomic mass of radon is 0.387387387… .
To convert the decimal 0.387387387… to a fraction,
Let

Question 11.
Convert \(\frac{1}{15}\) to a decimal. Write the decimal using an ellipsis, then write the decimal using an overbar.
Answer:
Ellipsis : 0.0666…,
Overbar : \(0 . 0\overline{6}\),

Explanation:
Given to convert \(\frac{1}{15}\) to a decimal using an ellipsis as we have \(\frac{1}{15}\) = 0.066666 as ellipsis is three dots to show repeating pattern continues,
as we have 6 is repeating so it is 0.0666…. now to write overbar for 6
as repeating \(0 . 0\overline{6}\).

Question 12.
Critique Reasoning Mitchell was asked to write 0.616161… as a fraction. His work is shown. Do you agree with his answer? If not, explain Mitchell’s error and correct it.

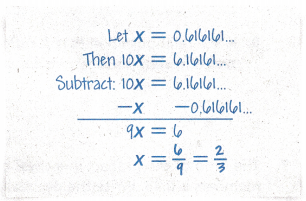
Answer:
No, I will not agree with Mitchell’s answer,

Explanation:
Given Mitchell was asked to write 0.616161… as a fraction.
His work is shown. I dont agree with his answer as it has error there are 2 repeating decimals so multiply both sides of the equation by 10² = 100, so that both equations have the same repeating digits to the right of the decimal point as

For Problems 13-18, write the number as a fraction or mixed number in simplest form.

Question 13.
4.024
Answer:
\(\frac{503}{125}\) or 4\(\frac{3}{125}\),

Explanation:
Given to write 4.024 as a fraction

As numerator is greater than denominator we write \(\frac{503}{125}\) in mixed fraction as 4\(\frac{3}{125}\).

Question 14.
-1.111…..
Answer:
–\(\frac{10}{9}\) or -1\(\frac{1}{9}\),

Explanation:
Given to convert -1.111….. negative decimal to a fraction remove the negative sign from the decimal number, Perform the conversion on the positive value, Applying the negative sign to the fraction answer if a = b then it is true that -a = -b. So

therefore -1.111….. decimal fraction is
–\(\frac{39}{9}\) or -1\(\frac{1}{9}\).

Question 15.
\(-0 . \overline{39}\)
Answer:
–\(\frac{33}{99}\) or –\(\frac{13}{33}\),

Explanation:
Given to convert \(-0 . \overline{39}\) negative decimal to a fraction
remove the negative sign from the decimal number Perform the conversion on the positive value,
Applying the negative sign to the fraction answer if a = b then it is true that -a = -b. So

Question 16.
\(0.61 \overline{4}\)
Answer:
\(\frac{553}{900}\),

Explanation:
To convert \(0.61 \overline{4}\) steps are, Let

Question 17.
2.484848…
Answer:
\(\frac{82}{33}\) or 2\(\frac{16}{33}\),

Explanation:
To convert 2.484848, Let

Question 18.
0.7222…
Answer:
\(\frac{65}{90}\),

Explanation:
Let x be the given decimal Writing an equation with the decimal. x = 0.72222….
Multiply by a power of 10 so that the first repeating digit appears just to the right of the decimal point.
10x = 7.2222….,
Then multiply both sides of the equation by 100. 100x = 72.222…..,
Subtract the expression equal to from both sides.
100x = 72.2222
-10x = -7.2222
90x = 65
x = \(\frac{65}{90}\).

I’m in a Learning Mindset!

How am I using formative feedback to solve problems about rational numbers?
Answer:
Focused on complex and challenging problem-solving tasks,
Working out practice problems more,

Explanation:
While solving problems about rational numbers, Focused on complex and challenging problem-solving tasks, Working out practice problems more.

Lesson 10.1 More Practice/Homework

Question 1.
Kara and Nathan participated in a 60-minute maze race.

A. Use ratio notation and decimal notation to describe the relationship between Kara’s time and the total time of the race.
Answer:
Ratio notation: 32:60, Decimal notation: \(0.5 \overline{3}\),

Explanation:
Given Kara and Nathan participated in a 60-minute maze race. As a ratio is written with a colon between the two quantities that are being compared as the relationship between Kara’s time and the total time of the race in ratio notation: 32: 60 and as decimal notation is the representation of a fraction using the base 10 along with a decimal point we have \(\frac{32}{60}\) = \(\frac{8}{15}\) = 0.5333333… so it is \(0.5\overline{3}\).

B. Is the relationship in Part A rational or irrational? Justify your answer.
Answer:
Yes, rational,

Explanation:
Relationship is rational
Justification:
As we know rational numbers are one very common type of number that we usually study
after integers in math. These numbers are in the form of p/q, where p and q can be any integer and q ≠ 0 and The word “Rational” is originated from the word “ratio”.
So, rational numbers are very well related to the ratio concept of ratio.
As the relationship in part A is ratio notation: 32: 60 or \(\frac{32}{60}\) = \(\frac{8}{15}\) it is rational and as we know non-terminating decimals with
repeating patterns of decimals are also rational numbers and
we have relationship in part A as \(0.5\overline{3}\) a non terminating decimals therefore the relationship is rational.

Question 2.
Math on the Spot Write the decimal \(0 . \overline{63}\) as a fraction in simplest form.
Answer:
\(\frac{7}{11}\),

Explanation:
Given to find decimal \(0 . \overline{63}\) as a fraction is

Question 3.
The average number of hourly visitors to an art exhibit is \(45.1 \overline{3}\). Write the average number of hourly visitors as a mixed number in simplest form.

Answer:
\(\frac{677}{15}\) or 45\(\frac{2}{15}\),

Explanation:
Given the average number of hourly visitors to an art exhibit is \(45.1 \overline{3}\).
The average number of hourly visitors as a mixed number in simplest form is to pass a periodic
decimal number to a mixed number, we must first pass it to a fraction, as follows:
The number is 45.13333, which is equal to 45.13 ~ where we know that 3 repeats infinitely many times. First we must subtract the number without a comma and the number without a comma without
ncluding the periodic number, like this: 4513 – 451 = 4062,
Then, divide by a number of nines, for each periodic number together with zeros for each non-periodic number (only the part after the comma). Ie .13 ~,
Because there is only one periodic (3) and non-periodic (1) number, it is divided by 90.
4062/90, we take out half 2031/45 then third 677/15, can no longer be reduced.
Now pass to a mixed number, we divide, the integer part would be the quotient, and the other part would be the fractional part, which would be the numerator the remainder and the denominator would be the number that divides like this we get 45\(\frac{2}{15}\).

Question 4.
Critique Reasoning Katrina said the number 0.101100111000… is a rational number because it consists only of the digits 0 and 1, and these digits repeat. Do you agree or disagree? Explain.
Answer:
Disagree,

Explanation:
Given Katrina said the number 0.101100111000… is a rational number because it consists only of the digits 0 and 1 and these digits repeat. I disagree as 0.101100111000… is
a infinite acyclic decimal, i.e, we cannot write it in form of p/q, p, q are  integers q ≠ 0, As it is not a rational number it is irrational number.

Question 5.
Convert \(\frac{1}{27}\) to a decimal. Write the decimal using an ellipsis, then write the decimal using an overbar.
Answer:
Ellipsis : 0.037037…, Overbar : \(0 . 0\overline{037}\),

Explanation:
Given to convert \(\frac{1}{27}\) to a decimal using an ellipsis as we have \(\frac{1}{27}\) = 0.0370370 as ellipsis is three dots to show repeating pattern continues,
as we have 037 is repeating so it is 0.037037…. now to write overbar for 037
as repeating \(0 . 0\overline{037}\).

Write the rational number as a fraction or mixed number in simplest form.

Question 6.
0.0606060…
Answer:
\(\frac{2}{33}\),

Explanation:
Given to convert 0.0606060… as a fraction Step 1: To convert 0.06 repeating into a fraction,
begin writing this simple equation: n = 0.06 (equation 1), Step 2: Notice that there are 2 digitss in the repeating block (06), so multiply both sides by 1 followed by 2 zeros, i.e., by 100.
100 × n = 6.06 (equation 2),
Step 3: Now subtract equation 1 from equation 2 to cancel the repeating block (or repetend) out.
100 × n = 6.06, 1 × n = 0.06,  99 × n = 6, 6/99 could be the answer, but it still we can put in the
simplest form, i.e., reduced.
To simplify this fraction, divide the numerator and denominator by 3 (the GCF – greatest common factor). n = 699 = 6 ÷ 399 ÷ 3 = 233. So, 0.060606…. = \(\frac{2}{33}\) as the lowest possible fraction.

Question 7.
-8.725
Answer:
–\(\frac{349}{40}\) or -8\(\frac{29}{40}\),

Explanation:
Given to convert -8.725 negative decimal to a fraction remove the negative sign from the decimal number, Perform the conversion on the positive value, Applying the negative sign to the fraction answer if a = b then it is true that -a = -b. So

Therefore –\(\frac{349}{40}\) or -8\(\frac{29}{40}\).

Question 8.
0.424242…
Answer:
\(\frac{42}{99}\),

Explanation:
Let x be 0.424242……., since same number is repeating after two digtits,
we just multiply 10² with x i.e 100x=42.424242…….,
100x – x = 42.424242…….
                   -0.424242…….
99x = 42, therefore x = \(\frac{42}{99}\).

Question 9.
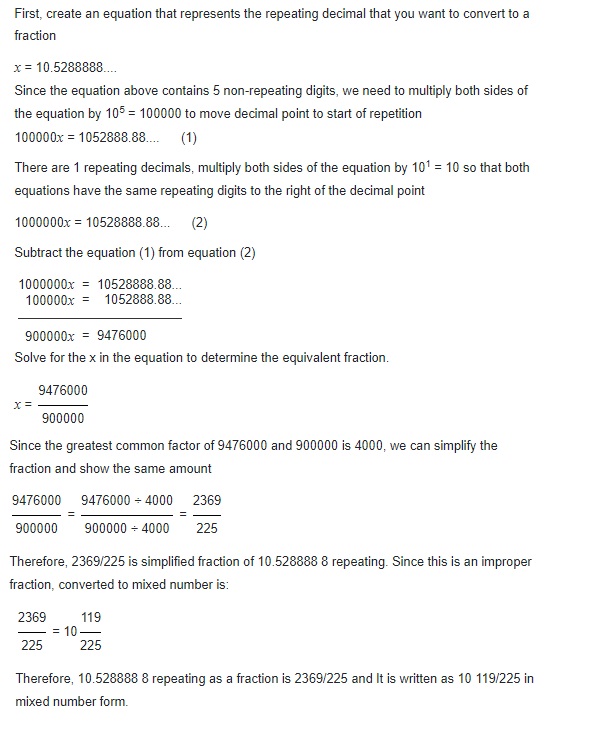
1.52888…
Answer:
\(\frac{2369}{225}\) or 10\(\frac{119}{225}\),

Explanation:
To convert 1.528888…. to a fraction,

Question 10.
\(-10 . \overline{7}\)
Answer:
–\(\frac{3233}{300}\) or -10\(\frac{233}{300}\),

Explanation:
Given to convert \(-10 . \overline{7}\) negative decimal to a fraction
remove the negative sign from the decimal number, Perform the conversion on the positive value,
Applying the negative sign to the fraction answer if a = b then it is true that -a = -b.

Applying the negative sign to the fraction answer is –\(\frac{3233}{300}\) or -10\(\frac{233}{300}\).

Question 11.
\(0 . \overline{57}\)
Answer:
\(\frac{19}{33}\),

Explanation:

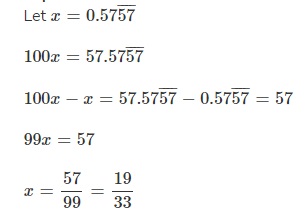
Therefore \(0 . \overline{57}\) as a fraction or mixed number in simplest form is \(\frac{19}{33}\).

Test Prep

Question 12.
Midori wrote a ratio of two integers. Which of the following must be true about the number Midori wrote?
(A) The decimal form of the number is a terminating decimal.
(B) The decimal form of the number is a repeating decimal.
(C) The number is rational.
(D) The number is irrational.
Answer:
(A) The decimal form of the number is a terminating decimal,
(B) The decimal form of the number is a repeating decimal,
(C) The number is rational,

Explanation:
Given Midori wrote a ratio of two integers ince any integer can be written as the ratio of two integers,
all integers are rational numbers. Remembering that all the counting numbers and all the whole numbers are also integers and so they, too, are rational,
And any number that can be represented as a repeating repeating or terminating decimal terminating, A rational number is a number that can be written as a ratio.
That means it can be written as a fraction, in which both the numerator (the number on top) and the denominator (the number on the bottom) are whole numbers.
Therefore bits (A) The decimal form of the number is a terminating decimal,
(B) The decimal form of the number is a repeating decimal and (C) The number is rational.

Question 13.
Which of the following is \(0 . \overline{15}\) written as a fraction in simplest form?
(A) \(\frac{1}{15}\)
(B) \(\frac{1}{9}\)
(C) \(\frac{3}{20}\)
(D) \(\frac{5}{33}\)
Answer:
(D) \(\frac{5}{33}\),

Explanation:
Given to find which of the following is \(0 . \overline{15}\) written as a fraction in simplest form so

therefore matches with bit (D) \(\frac{5}{33}\).

Question 14.
Paolo keeps track of his favorite baseball player’s batting average, and notices the average is 0.4727272… . If his player has 55 at bats, what is the number of hits?
_____________ hits
Answer:
Number of hits of Paolo favorite baseball player is 26,

In a survey of 120 people who visited a lake, 20% went fishing. Of those who went fishing, 75% also went swimming. Of those who did not go fishing, 50% went swimming. Use this information to solve Problems 15-16.

Question 15.
Construct a two-way frequency table to display the data.

Answer:

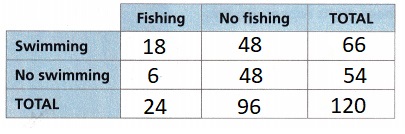
Explanation:
Given in a survey of 120 people who visited a lake 20% went fishing. Of those who went fishing, 75% also went swimming. Of those who did not go fishing,
50% went swimming. So constructed a two-way frequency table to display the data as  shown above.

Question 16.
What percent of those surveyed did not go swimming?
Answer:
45% did not go swimming,

Explanation:
From the two-way frequency table we got information that out of 120 people who visited a lake 54 people did not go swimming, so percent of those surveyed did not go swimming are \(\frac{54}{120}\) X 100 = 45%.

Question 17.
In the figure, line p is parallel to line q. Write an equation you can use to find the value of y, and explain why you can use it. Then solve the equation and use your result to help you find the measure of ∠1.

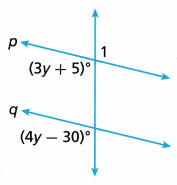
Answer:
Equation I can use to find the value of y is
(3y + 5)° = (4y – 30)°, y = 35°,
The measure of ∠1 = 110°,

Explanation:
Let us take the below shown figure, line L1 is parallel to line L2,
We know that if

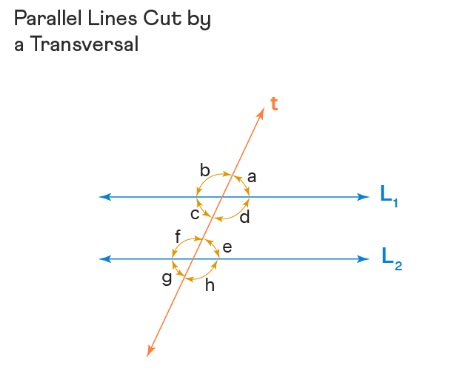
Corresponding Angles: It should be noted that the pair of
corresponding angles are equal in measure. In the figure, there are four pairs of corresponding angles that is, ∠a = ∠e, ∠b = ∠f, ∠c = ∠g, and ∠d = ∠h,
Alternate Interior Angles: Alternate interior angles are formed on the inside of two parallel lines that are intersected by a transversal. They are equal in measure, In this figure, ∠c = ∠e, ∠d = ∠f,
Alternate Exterior Angles: Alternative exterior angles are formed on either side of the transversal and
they are equal in measure. In this figure, ∠a = ∠g, ∠b = ∠h,
Consecutive Interior Angles: Consecutive interior angles or co-interior angles are formed on the inside of the transversal and they are supplementary. Here, ∠c + ∠f = 180°, and ∠d + ∠e = 180°,
Vertically Opposite Angles: Vertically opposite angles are formed when two straight lines intersect each other and they are equal in measure. Here, ∠a = ∠c, ∠b = ∠d, ∠e = ∠g, ∠f = ∠h,
If we see the given figure (3y + 5)° and (4y – 30)° are corresponding angles so we have  (3y + 5)° = (4y – 30)° solving y = 5°+ 30° = 35°, Now ∠c = (3y + 5)° = (3 X 35° + 5)° = 110°,
So ∠g = (4y – 30)° = (4 X 35° – 30°)°= 140°- 30° = 110° so ∠c = ∠g.
As we have alternative exterior angles as ∠c = ∠e and we have ∠a = ∠e as they are corresponding angles, therefore ∠c = ∠g means ∠c = ∠e = ∠a = ∠g are equal it means that ∠1 = 110°.