We included HMH Into Math Grade 8 Answer Key PDF Module 1 Lesson 2 Explore Translations to make students experts in learning maths.
HMH Into Math Grade 8 Module 1 Lesson 2 Answer Key Explore Translations
I Can translate figures, describe the translations using words and mapping notation, and determine an algebraic rule for translating a figure on a coordinate plane.

Spark Your Learning
The objective of chess is for one player’s pieces to capture the other player’s king. Each chess piece moves according to special rules.

Which move(s) will get any piece to land on a yellow, a blue, or a red dot? Two of the dots?

Answer:
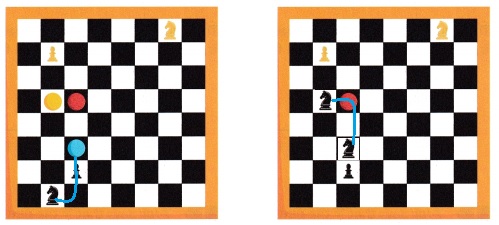
Explanation:
The objective of chess is for one player’s pieces to capture the other player’s king.
Each chess piece moves according to special rules.
From the above given information,
the black knight moves 1 space right and 2 spaces up,
then it reaches to blue dot and moves 2 spaces up and 1 space left to reach yellow dot.
Turn and Talk Move the black knight 1 space right and 2 spaces up. Then return the knight to its original location and move it 2 spaces up and 1 space right. What do you notice? Is this always true? Explain.
Answer:
No,
Explanation:
The knight is one of the most powerful pieces on the chessboard due to its unusual movement.
Understanding the basics of the knight can help to develop powerful openings in the beginning of the game and set you up for checkmate in the endgame.
Build Understanding
The figure that results from a transformation, such as a translation, is called the image. The original figure is called the preimage.
Connect to Vocabulary
A translation is the movement of a figure along a straight line.
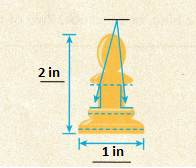
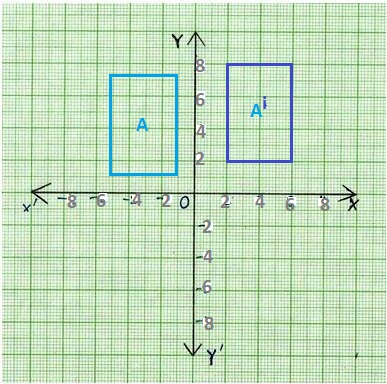
1. Aran says that if the pawn shown below is translated 2 inches right, the preimage and the image will have the same parallel line segments and will be the same height and width. Hiro says the parallel line segments will remain parallel but the height and width will not be the same. Who is correct?
A. Fill in the dimensions and angle measures. Are the dashed segments parallel? _____

Answer:
yes, Aran is correct.
Explanation:
If the pawn shown below is translated 2 inches right,
the preimage and the image will have the same parallel line segments,
and will be the same height and width.
B. Trace the pawn. Translate your tracing 2 inches right. What is the relationship between the dimensions, angle measures, and parallel segments of the preimage and image?
Answer:
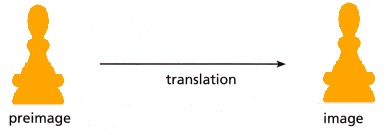
Explanation:
A preimage is the original figure in a transformation.
A transformation is a change in the position, size, or shape of a new geometric figure.
The preimage of a transformation is the shape before the transformation
The new figure is called the image and original figure is known as preimage.
C. Which student is correct? _______________
Answer:
Aran is correct,
Explanation:
Aran says that if the pawn shown below is translated 2 inches right,
the preimage and the image will have the same parallel line segments and,
will be the same height and width is correct.
D. What translation must Aran perform on the image so that it returns to the exact location of the preimage?
Answer:
The transformation that takes each point in a figure,
and slides it the same distance in the same direction.
Explanation:
In a translation, every point of the object must be moved in the same direction and the same distance.
When you are performing a translation, the initial object is called the pre-image,
and the object after the translation is called the image.
Turn and Talk Does the direction or distance a figure is translated affect the side lengths, relationships between sides, or angle measures of the figure? Explain.
Answer:
NO,
Explanation:
In a translation, every point of the object must be moved in the same direction and for the same distance.
When you are performing a translation, the initial object is called the pre-image,
and the object after the translation is called the image.
Step It Out
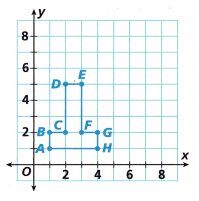
2. Hiro draws a sketch of a game piece on a coordinate plane. Then he translates it 3 units right and 3 units up.
A. Draw the image of Figure ABCDEFGH on the coordinate plane after it is translated 3 units right and 3 units up.
Answer:
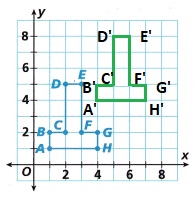
Explanation:
As shown above the figure ABCDEFGH on the coordinate plane,
is translated 3 units right and 3 units up.
The resultant polygon is shown in the above graph A’B’C’D’E’F’G’H’ in green color.
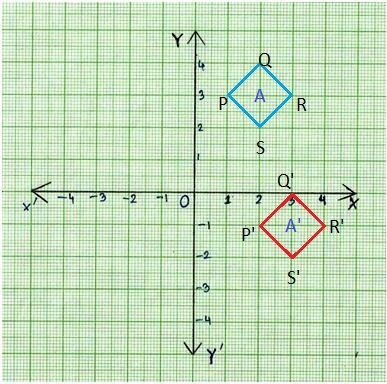
B. Prime notation, adding apostrophes to each letter label, is used to label images. For instance, Point A in the preimage is labeled A’ in the image and read as “A prime.” Label the image you drew using prime notation.
Answer:

Explanation:
A transformation is an operation that moves, flips, or changes a shape to create a new shape.
A translation is a type of transformation that moves each point in a figure,
the same distance in the same direction.
The figure ABCDEFGH on the coordinate plane, is translated 3 units right and 3 units up.
The resultant polygon is shown in the above graph A’B’C’D’E’F’G’H’ in green color.
C. Complete the table of ordered pairs.

Answer:

Explanation:
A preimage is the original figure in a transformation.
A transformation is a change in the position, size, or shape of a new geometric figure.
The preimage of a transformation is the shape before the transformation
The new figure is called the image and original figure is known as preimage.
D. What do you notice about the relationship between the x- and y-values of each vertex of the preimage compared to the x- and y-values of each vertex of the image?
Answer:
sliding factor 3.
Explanation:
Sliding of image is observed in the above image and pre image.
The relationship between the x- and y-values of each vertex of the preimage.
Compared to the x- and y-values of each vertex of the image.
E. Translations in the coordinate plane can be described in mapping notation as (x, y) → (x ± a, y ± b) where a is the number of units the figure is translated horizontally and b is the number of units the figure is translated vertically. You read this notation as, “The ordered pair x, y is mapped to the ordered pair x plus or minus a, y plus or minus b.”
Describe the translation of Figure ABCDEFGH using mapping notation, (x, y) → (x + ___, y + ___)
Answer:
Mapping notation as (x, y) → (x ± a, y ± b).
Explanation:
a is the number of units the figure is translated horizontally and,
b is the number of units the figure is translated vertically.
a = 3 and b = 3
The ordered pair x, y is mapped to the ordered pair x plus or minus a, y plus or minus b.
The translation of Figure ABCDEFGH using mapping notation, (x, y) → (x + 3, y + 3)

F. What do you notice about the size, shape, angle measures, and relationship between the sides in the preimage and image?
Answer:
No change in the size, shape, angle measures.
Explanation:
The relationship between the sides in the preimage and image.
Only position is shifted by a factor of 3 for both x and y coordinated.
Turn and Talk If Figure ABCDEFGH is translated using the rule (x, y) → (x — 2, y — 4), how does the image of this translation compare to the image of the translation described in Task 2?
Answer:
![]()
Explanation:
ABCDEFGH is translated using the rule (x, y) → (x — 2, y — 4),
the image of this translation compare to the image of the translation described in Task 2.
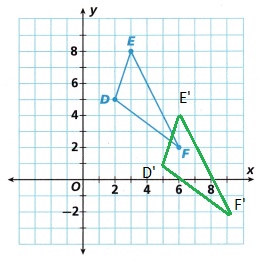
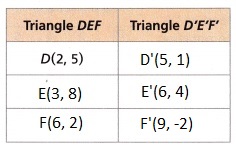
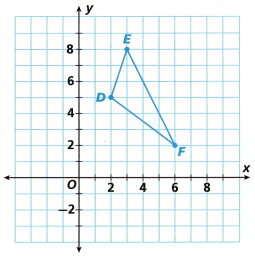
3. Triangle DEF is translated using the rule (x, y) → (x + 3, y — 4).
A. Use words to describe the distance and direction Triangle DEF is translated.
Answer:
Triangle DEF is translated as shown below the figure,
the new co ordinates are using the rule (x, y) → (x + 3, y — 4).
Explanation:
The triangle is translated using the rule (x, y) → (x + 3, y – 4),
the given vertices of a triangle are (2, 2), (4. 5), and (6. 1).
By moving 3 units right and 4 units down wards direction the preimage translated,
and the new vertices of a triangle are noted in the above table.
B. Draw the image. Label it using prime notation.
Answer:

Explanation:
All the co ordinates of the preimage are market on the graph to pot a triangle
The triangle is translated using the rule (x, y) → (x + 3, y – 4),
the given vertices of a triangle are (2, 2), (4, 5), and (6.,1).
By moving 3 units right and 4 units down wards direction the preimage translated,
and new triangle image is formed.
C. Complete the table.

Answer:


Explanation:
The triangle is translated using the rule (x, y) → (x + 3, y – 4),
the given vertices of a triangle are (2, 2), (4, 5), and (6, 1).
By moving 3 units right and 4 units down wards direction the preimage translated.
Check Understanding
Question 1.
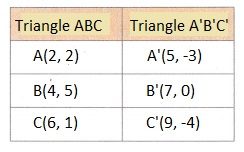
The coordinates of a triangle’s vertices are (2, 2), (4. 5), and (6. 1).
A. If the triangle is translated using the rule (x, y) → (x + 3, y – 5), by how many units and in what direction was the preimage translated?
____________________
Answer:
Explanation:
the triangle is translated using the rule (x, y) → (x + 3, y – 5),
the given vertices of a triangle are (2, 2), (4, 5), and (6, 1).
By moving 3 units right and 5 units down wards the preimage translated,
the new vertices of a triangle are noted in the above table.
B. What are the coordinates of the image’s vertices?
____________________
Answer:
New co ordinates are,
A'(5, -3), B'(7, 0) and C'(9, -4)
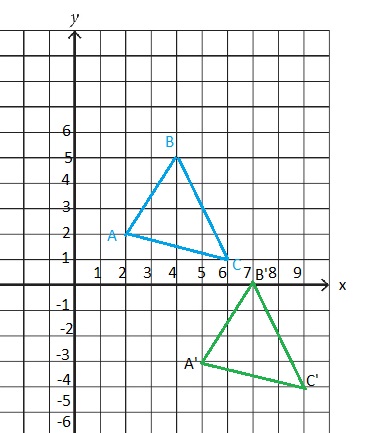

Explanation:
The triangle is translated using the rule (x, y) → (x + 3, y – 5),
the given vertices of a triangle are (2, 2), (4, 5), and (6, 1).
By moving 3 units right and 5 units down wards direction the preimage translated,
the new vertices of a triangle are noted in the above table.
C. Write a true statement about the relationship of the line segments and angle measures when a translation is applied to a preimage.
Answer:
Line AB and line A’B’ are parallel to each other and the angle ACB and A’C’B’ are congruent.
Explanation:
The two figures or objects are congruent if they have the same shape and size,
or if one has the same shape and size as the mirror image of the other.
Line AB and line A’B’ are parallel to each other and the angle ACB and A’C’B’ are congruent is a true,
about the relationship of the line segments and angle measures,
when a translation is applied to a preimage.
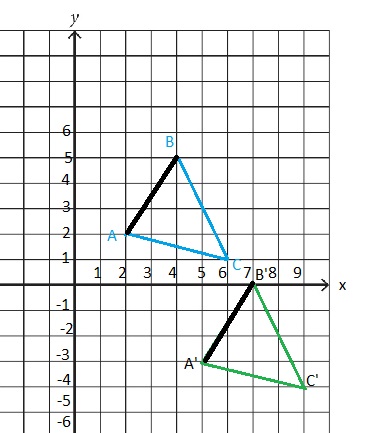
D. Will the line segment between (2, 2) and (4, 5) be parallel to its image?
____________________
Answer:
Yes,
Explanation:
The line segment between (2, 2) and (4, 5) be parallel to its image (5, -3) and (7, 0),
as shown in the below diagram in dark black lines.
Question 2.
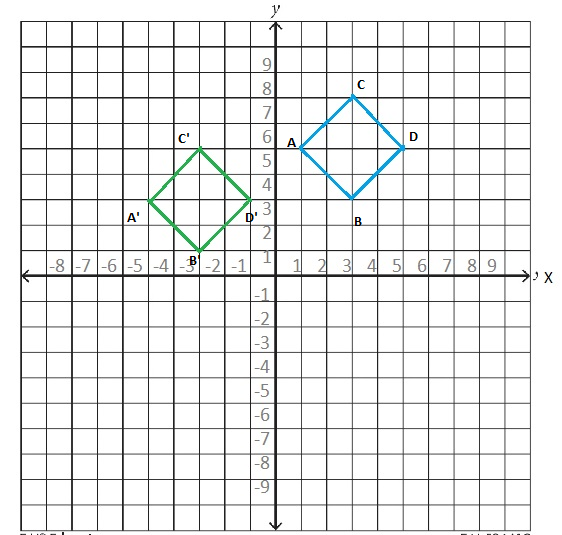
The coordinates of the vertices of the preimage of a parallelogram are (1, 5), (3, 3), (3, 7), and (5, 5). The coordinates of the vertices of the image are (-5, 3), (-3, 1), (-3, 5), and (-1, 3). How far and in what direction was the parallelogram translated? Write your answer using mapping notation and practice reading your answer aloud.
Answer:
6 units down and 2 units left.
Explanation:
The vertices of the preimage of a parallelogram are A(1, 5), B(3, 3), C(3, 7), and D(5, 5).
the triangle is translated using the rule (x, y) → (x – 6, y – 2)
The coordinates of the vertices of the image are A'(-5, 3), B'(-3, 1), C'(-3, 5), and D'(-1, 3).
On Your Own
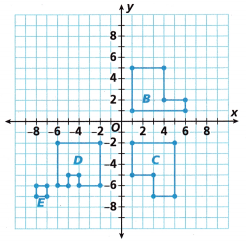
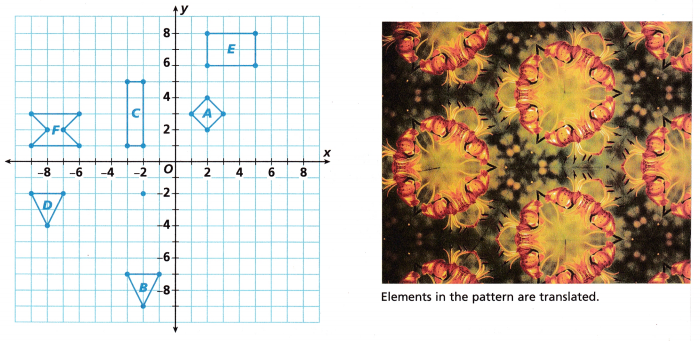
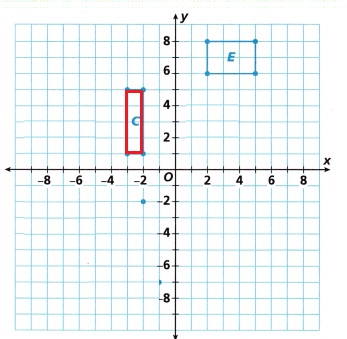
Solve Problems 3-5 using the graph of Buildings A, B, C, D, and E.
Question 3.
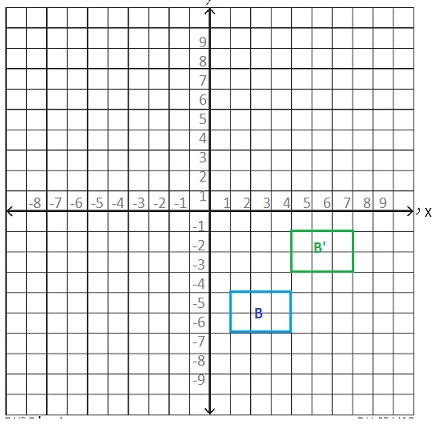
Shana translates Building B three units right and three units up. Draw the image of Building B in the new location.

Answer:
The triangle is translated using the rule (x, y) → (x + 3, y + 3),
the image of Building B in the new location.
Explanation:
A preimage is the original figure in a transformation.
A transformation is a change in the position, size, or shape of a new geometric figure.
The preimage of a transformation is the shape before the transformation
The new figure is called the image and original figure is known as preimage.
When we move three units right and three units up the resultant image is shown in the above graph.
Question 4.
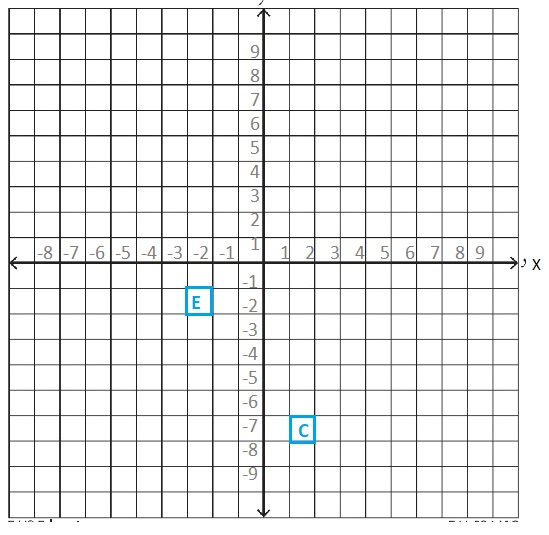
Model with Mathematics Shana translates Building C to the location of Building E. Use mapping notation to describe the translation of Building C.
Answer:
Explanation:
The triangle is translated using the rule (x, y) → (x – 4, y + 5),
the image of Building B in the new location.
A(1, -6)
(x, y) → (x – 4, y + 5)
A'(-3, -1)
Question 5.
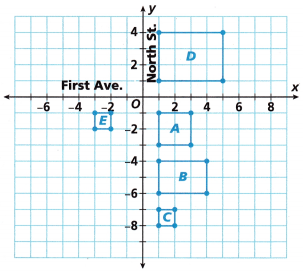
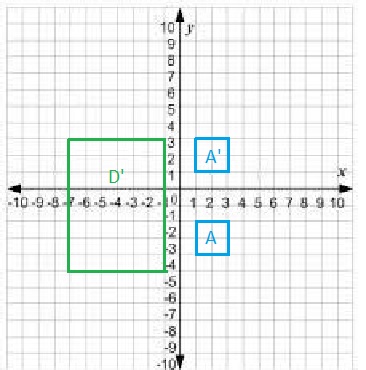
Construct Arguments The coordinates of the vertices of the image of Building D are (-7, 3), (-1, 3), (-1, -5), and (-7, -5). The coordinates of the vertices of the image of Building A are (1, 1), (3, 1), (3, 3), and (1, 3). Which of these is not a translation of the preimage? Explain by using the definition of a translation.
Answer:
The coordinates of the vertices of the image of Building are,
A (1, 1), (3, 1), (3, 3), and (1, 3) is true and is shown in the below graph.
The coordinates of the vertices of the image of Building are,
D (-7, 3), (-1, 3), (-1, -5), and (-7, -5) is not a translation of the preimage,
as coordinates are not satisfying the definition of transformation.
Explanation:
A translation is a transformation that slides a figure.
The transformation that takes each point in a figure,
and slides it the same distance in the same direction.
In a translation, every point of the object must be moved in the same direction and for the same distance.
When you are performing a translation, the initial object is called the pre-image,
and the object after the translation is called the image.
Use the triangles shown to answer Problems 6—7. Triangle 2 is a translation of Triangle 1.
Question 6.
All the sides of Triangle 1 have a length of 3 inches. What is the length each side of Triangle 2? _______________
Answer:
The length of each triangle is 3 inches.
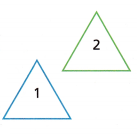
Explanation:
In equilateral triangle all the sides of triangle are same.
In triangle 1 the length of each side is 3 inches.
So, the length of each side is also 3 inches in triangle 2.
As, both the triangles are mirror images.
Question 7.
All the angles of Triangle 1 have a measure of 60°. What is the measure each angle of Triangle 2? _______________
Answer:
60 degrees.
Explanation:
Reflection of transformation takes place.
As we know reflection is also known as flip.
In equilateral triangle each angle is of 60 degrees.
Use the description shown to answer Problems 8—9.
Square P’Q’R’S’ is a translation of Square PQRS.
Question 8.
What is true about the angles of Square PQRS and Square P’Q’R’S’?
_______________
Answer:
Yes,
The angles of Square PQRS and Square P’Q’R’S’ are same.
Explanation:
A translation is a type of transformation that takes each point in a figure and,
slides it the same distance in the same direction.
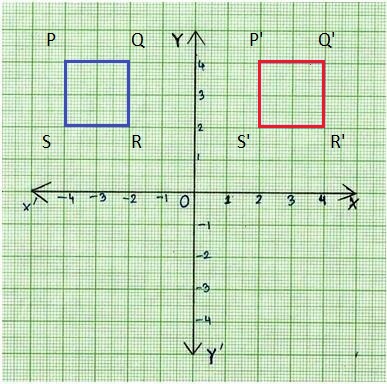
as shown in the above figure.
Square PQRS and Square P’Q’R’S’ are mirror images.
Here, transformation of reflection takes place.
So, there is no change in the angles.
Question 9.
Opposite sides of Square PQRS are parallel and the same length. What is true about opposite sides of Square P’Q’R’S?
Answer:
Yes,
The opposite sides of square PQRS are parallel and the same length.
Explanation:

as shown in the above figure.
A square has 4 sides of equal length and opposite sides are parallel.
So a square can also be classified as a parallelogram.
Square PQRS and Square P’Q’R’S’ are mirror images.
Here, transformation of reflection takes place.
So, there is no change in the angles.
Solve Problems 10-13 using the graph of Houses B, C, D, and E.
Question 10.
Attend to Precision House B is translated using the rule (x, y) → (x – 3, y + 2). Draw House B in its new location.

Answer:
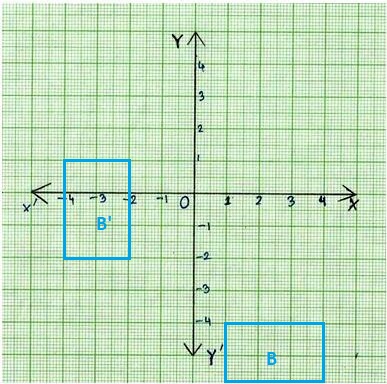
Explanation:
The coordinates of the vertices of the image of Building B are (1, -4), (1, -6), (4, -4), and (4, -6).
House B’ is translated using the rule (x, y) → (x – 3, y + 2).
The coordinates of the vertices of the image of Building B’ are (-2, -2), (-2, -4), (1, -2), and (1, -4).
Question 11.
Model with Mathematics The builder adds House A to her plan first with vertices at (-1, 1), (-5, 1), (-5, 7), and (-1, 7). Then she moves it so it has vertices at (6, 2), (2, 2), (2, 8), and (6, 8). Use mapping notation to describe how far and in what direction she translated the house.
_____________
Answer:
7 units in the right side direction and 1 unit up.
Explanation:
The coordinates of the vertices of the image of Building A are (-1, 1), (-5, 1), (-5, 7), and (-1, 7).
House A’ is translated using the rule (x, y) → (x + 7, y + 1).
The coordinates of the vertices of the image of Building A’ are (6, 2), (2, 2), (2, 8), and (6, 8).
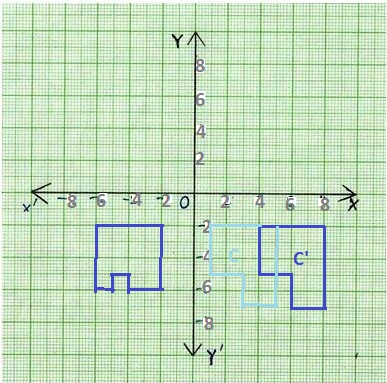
Question 12.
In its final location, House C has vertices at (4, -2), (4, -5), (6, -5), (6, -7), (8, -7), and (8, —2). In its final location, House D has vertices at (-2, -2), (-6, -2), (-6, -6), (-5, -6), (-5, -5), (-4, -5), (-4, -6), and (-2, -6).
Which building represents a translation from its original placement? Explain.
Answer:
Building C’ represents a translation from its original building C placement.
House C’ is translated using the rule (x, y) → (x + 3, y).
Explanation:
In its final location, House C has vertices at (4, -2), (4, -5), (6, -5), (6, -7), (8, -7), and (8, —2).
In its final location, House D has vertices at,
(-2, -2), (-6, -2), (-6, -6), (-5, -6), (-5, -5), (-4, -5), (-4, -6), and (-2, -6).
Question 13.
Building E is a shed. It is translated 1 unit left and 2 units up. Draw Building E in its new location.
Answer:
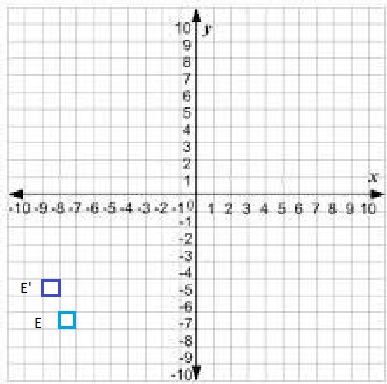
Explanation:
Figure E is translated using the rule (x, y) → (x-1, y+2).
A translation is a type of transformation that takes each point in a figure,
and slides it the same distance in the same direction.
Figure A is translated to Figure B is translated using the rule (x, y) → (x-1, y+2)
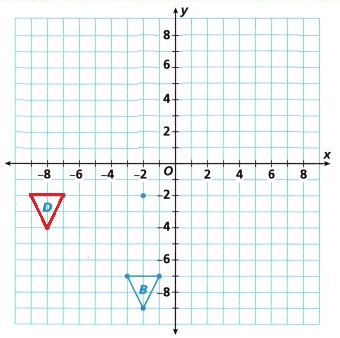
Question 14.
Is Figure B a translation of Figure A? Explain.
Answer:
Figure B is translated using the rule (x, y) → (x/2, y/3).
Explanation:
A translation is a type of transformation that takes each point in a figure,
and slides it the same distance in the same direction.
Figure A is translated to Figure B is translated using the rule (x, y) → (x/2, y/3).
I’m in a Learning Mindset!
How does my mindset affect my ability to successfully translate figures?
Answer:
The mindset affect my ability to successfully translate figures as,
In a translation, every point of the object must be moved in the same direction and for the same distance.
When you are performing a translation, the initial object is called the pre-image,
and the object after the translation is called the image.
Lesson 1.2 More Practice/Homework
Use the graph to answer Problems 1-4.
Question 1.
Translate Figure A using the rule (x, y) → (x + 1, y – 4). Draw the image of Figure A. Practice reading the rule aloud.
Answer:
Explanation:
Figure A using the rule (x, y) → (x + 1, y – 4).
Based on the rule the above figure is translated.
A translation is a type of transformation that takes each point in a figure,
and slides it the same distance in the same direction.
Question 2.
How was Figure B translated to get Figure D? Write your answer using mapping notation.
Answer:
Using mapping notation,
the figure is translated using the rule (x, y) → (x – 6, y + 5) as shown below,
Explanation:
A translation is a type of transformation that takes each point in a figure,
and slides it the same distance in the same direction.
Mapping Rule A mapping rule has the following form (x,y) → (x – 6, y + 5),
and tells you that the x and y coordinates are translated to x−6 and y+5.
Translations are also known as slides.
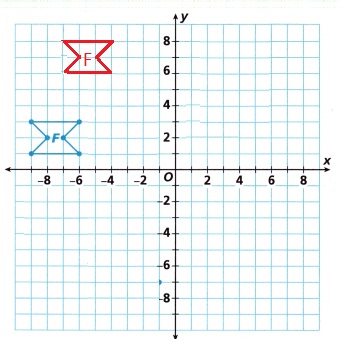
Question 3.
Construct Arguments Why is Figure E not a translation of Figure C?
Answer:
Figure E is not same size or shape of figure C.
Explanation:
Because both the polygons are different in their size and shape,
as shown in the below figures.
Question 4.
Figure F has vertices with coordinates at (-6, 1), (-9, 1), (-8, 2), (-9, 3), (-6, 3), and (-7, 2). If the figure is translated using the rule (x, y) → (x + 2, y + 5), what are the coordinates of the new vertices?
Answer:
The coordinates of the new vertices are,
(-4, 6), (-7, 6), (-6, 7), (-7, 8), (-4, 8), and (-5, 7).
Explanation:
Figure F has vertices with coordinates at (-6, 1), (-9, 1), (-8, 2), (-9, 3), (-6, 3), and (-7, 2).
The figure is translated using the rule (x, y) → (x + 2, y + 5).
The coordinates of the new vertices are,
(-6, 1) → (-6 + 2, 1 + 5) → (-4, 6),
(-9, 1) → (-9 + 2, 1 + 5) → (-7, 6),
(-8, 2) → (-8 + 2, 2 + 5) → (-6, 7),
(-9, 3) → (-9 + 2, 3 + 5) → (-7, 8),
(-6, 3) → (-6 + 2, 3 + 5) → (-4, 8),
(-7, 2) → (-7 + 2, 2 + 5) → (-5, 7).
Question 5.
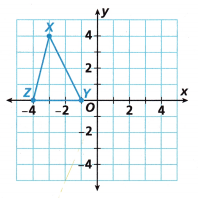
Math on the Spot Graph the translation Y of ∆XYZ 4 units right and 2 units down.
Answer:
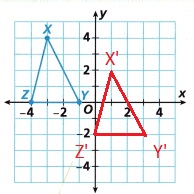
Explanation:
Graph the translation Y of ∆XYZ 4 units right and 2 units down.
Figure ∆XYZ has vertices with coordinates at X(-3, 4), Y(-1, 0) and Z(-4, 0).
The figure is translated using the rule is 4 units right and 2 units down.
(x, y) → (x + 4, y – 2),
The coordinates of the new vertices are,
(-3, 4) → (-3 + 4, 4 – 2) → (1, 2),
(-1, 0) → (-1 + 4, 0 – 2) → (3, -2),
(-4, 0) → (-4 + 4, 0 – 2) → (0, -2),
Test Prep
Question 6.
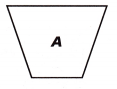
Which figure is a translation of Figure A?
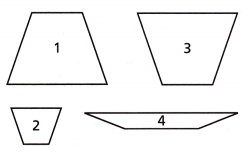
A. Figure 1
B. Figure 2
C. Figure 3
D. Figure 4
Answer:
Option (C)
Explanation:
Figure 3 is the translation of Figure A.
A translation is a type of transformation that takes each point in a figure,
and slides it the same distance in the same direction.
Question 7.
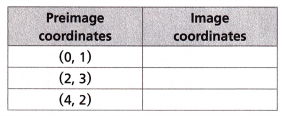
The coordinates of a triangle are given in the table.
The triangle is translated using the rule (x, y) → (x – 3, y + 2). What are the coordinates of the image of the triangle?
Answer:
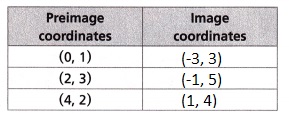
Explanation:
A transformation is a change in the position, size, or shape of a new geometric figure.
The preimage of a transformation is the shape before the transformation
The new figure is called the image and original figure is known as preimage.
The triangle is translated using the rule (x, y) → (x – 3, y + 2).
the coordinates of the new vertices are
(0, 1) → (0 – 3, 1 + 2) → (-3, 3),
(2, 3) → (2 – 3, 3 + 2) → (-1, 5),
(4, 2) → (4 – 3, 2 + 2) → (1, 4),
Question 8.
A quadrilateral is translated 5 units right and 3 units down on a coordinate plane. Which expressions could be used to find one of the coordinates of the vertices of the image? Select all that are correct.
A. x – 3
B. x – 5
C. x + 5
D. y – 3
E. y + 3
F. x + 5
G. y + 5
Answer:
Option (C) and (D)
Explanation:
The A quadrilateral is translated using the rule (x, y) → (x + 5, y – 3).
So, the coordinates of the new vertices are (x + 5, y – 3).
C. x + 5
D. y – 3
Spiral Review
Question 9.
You and 19 other people are entered in a drawing. One person will be randomly selected to win a prize. What is the probability that you will win the prize?
Answer:
0.05 or \(\frac{1}{20}\)
Explanation:
Total number of people along with me,
19 + 1 = 20
If one person will be randomly selected to win a prize.
The probability that I will win the prize,
= \(\frac{1}{20}\)
= 0.05
Question 10.
Ten red cards and ten black cards are placed in a bag. You choose one card and then another without replacing the first card. What is the probability that the first card will be red and the second card will be black?
Answer:
\(\frac{5}{19}\)
Explanation :
No of black cards = 10
No of red cards = 10
Probability of choosing a red card = no of red cards ÷ total number of cards
= \(\frac{10}{20}\) = \(\frac{1}{2}\)
No of cards remaining after choosing the red card = 20 – 1 = 19
Probability of choosing a black card with out replacing = no of black cards ÷ number of cards remaining
= \(\frac{10}{19}\) * \(\frac{1}{2}\)
= \(\frac{5}{19}\)
Question 11.
Seamus solves 100 randomly generated math problems that each use one of addition, subtraction, multiplication, or division. Predict the number of division problems Seamus solves.
Answer:
25 problems.
Explanation:
Seamus solves 100 randomly generated math problems,
that each use one of addition, subtraction, multiplication, or division.
The number of division problems Seamus solves,
= \(\frac{100}{4}\)
= 25 problems.