Into Math Grade 8 Module 1 Answer Key Transformations and Congruence

We included HMH Into Math Grade 8 Answer Key PDF Module 1 Transformations and Congruence to make students experts in learning maths.

HMH Into Math Grade 8 Module 1 Answer Key Transformations and Congruence

Puzzle Designer
A puzzle designer combines creativity and imagination with logical reasoning to make challenging and entertaining puzzles. From three-dimensional puzzles to jigsaw puzzles to mazes to crossword puzzles, puzzle designers have something to intrigue just about everyone.

STEM Task:
Starting with 12 toothpicks arranged as shown, perform each task:

• Remove 4 tooth picks to form exactly 1 square.
• Remove 4 toothpicks to form exactly 2 squares.
• Move 3 toothpicks to form exactly 3 squares.

Answer:
Remove 4 tooth picks to form exactly 1 square.

• 
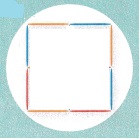
•   Remove 4 toothpicks to form exactly 2 squares.
• 
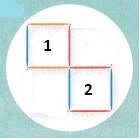
• Move 3 toothpicks to form exactly 3 squares.
  

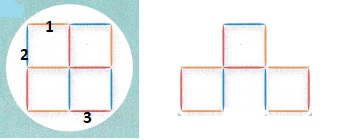
Explanation:
For two polygons to be congruent, they must have exactly the same size and shape.
This means that their interior angles and sides must all be congruent.
That’s why studying the congruence is so important to draw conclusions,
about the congruence of polygons.
Transformation function to make our lives easier and more convenient.
Their uses are truly relevant as they add efficiency in our work and lifestyle.
Not only that, they are also used in many fields as a form of art and design,
so that objects possess more beauty and personality.

Learning Mindset

Challenge-Seeking Builds Confidence

Have you ever been asked to do something that you didn’t know how to do? This happens to everyone at one time or another. Sometimes, people back away from a challenge because they are afraid of making a mistake. But taking on a challenge can be a rewarding growth experience. Here are two suggestions that can help you overcome a challenge when your confidence is fading.

• Build your confidence by trying simpler versions of the task. Think of learning to draw, dance, or build furniture. Succeeding at simple skills when you start gives you confidence to take on advanced challenges.
• Don’t give up. Remember, you are learning and growing through this process. A positive attitude will make this and future challenges easier to meet.

Reflect

Question.
Did you feel confident as you worked on the STEM Task?
Answer:
Yes,
Explanation:
Its interesting in solving puzzles which improves mindset confidence levels.
Students learn through interactive collaboration, exploration, and discovery.
This type of learning can help foster the confidence of special needs learners.

Question.
How does self-confidence affect your ability to complete tasks or meet challenges?
Answer:
Solving puzzles improves self-confidence and affect our ability to complete tasks or meet challenges.
Explanation:
Self-confidence beliefs, defined as people’s judgments of their capability to perform,
specific tasks are a product of a complex process of self-persuasion.

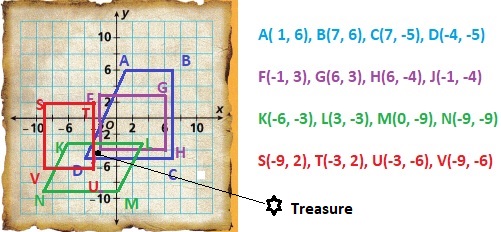
Treasure Hunt

A treasure is on a remote island represented by the coordinate plane.

Graph the following polygons.
A. ABCD with A( 1, 6), B(7, 6), C(7, -5), D(-4, -5)
B. FGHJ with F(-1, 3), G(6, 3), H(6, -4), J(-1, -4)
C. KLMN with K(-6, -3), L(3, -3), M(0, -9), N(-9, -9)
D. STUV with S(-9, 2), T(-3, 2), U(-3, -6), V(-9, -6)
E. Clues: The treasure is at a point with integer coordinates. The treasure is buried inside a trapezoid that is not a parallelogram, outside any squares or rectangles, and inside a parallelogram.
Where is the treasure buried? Explain how you know.

Turn and Talk
How did you use the clues to find the treasure?
Answer:
First plot the graph by using the co ordinates given on the cartesian co ordinate plane.

Explanation:
The most common way to give treasure hunt clues is to create a trail,
so that the answer to one clue reveals the next one.

Are You Ready?

Complete these problems to review prior concepts and skills you will need for this module.

Polygons in the Coordinate Plane

Draw each polygon in the coordinate plane.

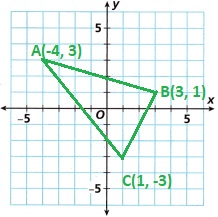
Question 1.
Triangle ABC has vertices
A(-4, 3), 8(3, 1), and C(1, -3).

Answer:

Explanation:
The horizontal axis is labeled as the x-axis and the vertical is the y-axis.
Triangle ABC has vertices
A(-4, 3), 8(3, 1), and C(1, -3).
On the Cartesian coordinate plane, everything is based on two number lines,
one that is horizontal x-axis and one that is vertical y-axis for the above ABC co-ordinates.

Question 2.
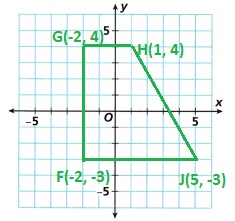
Quadrilateral FGHJ has vertices
F(-2, -3), G(-2, 4), H(1, 4), and J(5, -3).

Answer:

Explanation:
The horizontal axis is labeled as the x-axis and the vertical is the y-axis.
Quadrilateral FGHJ has vertices
F(-2, -3), G(-2, 4), H(1, 4), and J(5, -3).
On the Cartesian coordinate plane, everything is based on two number lines,
one that is horizontal x-axis and one that is vertical y-axis for the above FGH co-ordinates.

Draw Shapes with Given Conditions

Use a ruler and protractor to draw a quadrilateral that matches each description. Label the sides or angles described.

Question 3.
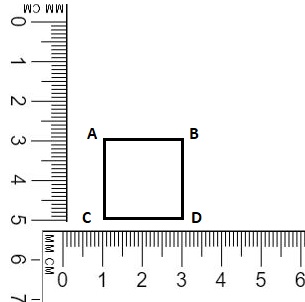
a square with a side length of 2 centimeters
Answer:

Explanation:
Placing a ruler at a square with a side length of 2 centimeters.
marking points A, B, C and D as shown above with a distance of measures 2cm,
Angle between AC and CD is 90°,
Angle between BD and AB is 90°.

Question 4.
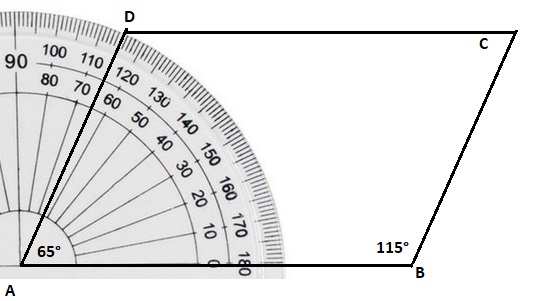
a parallelogram with two angles that measure 65° and two angles that measure 115°
Answer:

Explanation:
Placing a ruler at a parallelogram with two angles that measure 65° and two angles that measure 115°,
marking points A, B, C and D as shown above.
Angle between AB and AD  is 65° degrees.
Angle between BC and DC is 115° degrees.

Use a ruler and protractor to draw a triangle that matches each description. Label the sides or angles described.

Question 5.
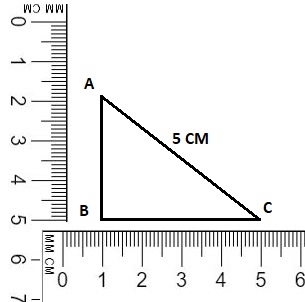
a right triangle with sides that measure 3 centimeters, 4 centimeters, and 5 centimeters
Answer:

Explanation:
Placing a ruler at an right angle triangle 90° at point B.
marking points A, B and C as shown above with a distance of measures,
3 centimeters A to B, 4 centimeters B to C, and 5 centimeters A to C.

Question 6.
a triangle with two angles measuring 70° and the side between them measuring 3 centimeters
Answer:

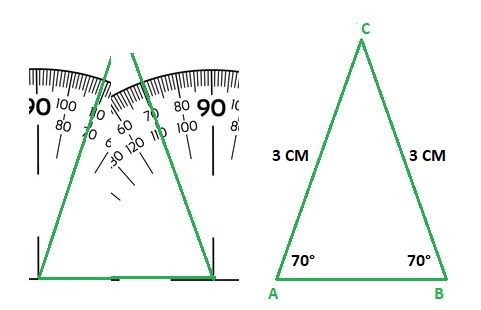
Explanation:
Using protractor and ruler for angle 70° and 3 cm length from A to C and B to C as shown above figure,
first mark the point on the plane paper and join the point.