We included HMH Into Math Grade 7 Answer Key PDF Module 9 Lesson 2 Draw and Construct Triangles Given Side Lengths to make students experts in learning maths.
HMH Into Math Grade 7 Module 9 Lesson 2 Answer Key Draw and Construct Triangles Given Side Lengths
I Can determine whether three lengths could be side lengths of a triangle, and, given two side lengths, I can find the range of possible lengths for the third side.
Spark Your Learning
Martina is building a wind chime. She has pieces of metal pipe 2, 3, 4, and 5 inches long that she is going to use to make a triangular top for the wind chime. Which combinations of three lengths will not work to make the top?

Answer:
2 in, 3 in and 5 in will not work.
Explanation:
The sum of all the angles of a triangle (of all types) is equal to 180°.
The sum of the length of the two sides of a triangle is greater than the length of the third side.
In the same way, the difference between the two sides of a triangle is less than the length of the third side.
The side opposite the greater angle is the longest side of all the three sides of a triangle.
Turn and Talk What do you notice about the set of lengths that did not make a triangle?
Answer:
The sum of the length of the two sides of a triangle is equal to the length of the third side.
2 + 3 = 5
Build Understanding
Question 1.
Can you draw a triangle with side lengths of 3, 4, and 8 units? There are different ways to model the situation and investigate. You can use thin strips of paper cut to the correct lengths, or you can use tools such as a ruler and compass, or geometry software.

A. Use the longest side of your model as the possible base. Use your model to view the shorter sides in different positions. Can you draw a triangle? If so, draw one. If not, explain why you cannot.
Answer:
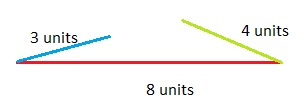
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
In the same way, the difference between the two sides of a triangle is less than the length of the third side.
The side opposite the greater angle is the longest side of all the three sides of a triangle.
The sum of the length of the two sides of a triangle is equal to the length of the third side.
3 + 4 = 7 units
the sum should be more than 8 units.
B. Repeat Part A using the shortest segment as the possible base. Can you draw a triangle? If so, draw one. If not, explain why you cannot.
Answer:
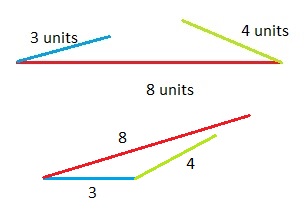
Explanation:
The sum of the length of the two sides of a triangle is equal to the length of the third side.
3 + 4 = 7 units
the sum should be more than 8 units.
C. Complete the statements describing the relationship among the three side lengths that do not form a triangle. Use less than, equal to, or greater than.
The sum of the lengths of the two shorter sides is ___________ the length of the longer one.
Answer:
Greater
Explanation:
The sum of the lengths of the two shorter sides is greater the length of the longer one.
Question 2.
Can you draw a triangle with side lengths of 3, 4, and 6 units?
A. Use the 6-unit segment of your model as the possible base. Can you make a triangle? If so, draw it. If not, explain why you cannot.
Answer:
Yes, we can draw a triangle.
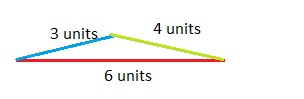
Explanation:
The sum of the length of the two sides of a triangle is greater then the length of the third side.
3 + 4 > 6 units
the sum should be more than 8 units.
B. Use the 3-unit segment as the possible base. Can you make a triangle? If so, draw it. If not, explain why you cannot.
Answer:
yes, it is possible
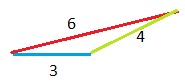
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
3 + 4 > 6 units.
C. Use the 4-unit segment as the possible base. Can you make a triangle? If so, draw it. If not, explain why you cannot.
Answer:
Yes, we can draw a triangle.

Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
3 + 4 > 6 units.
D. How are the triangles you made in Parts A-C alike?
Answer:
Length of the triangles are same but the shapes changes as shown below



E. Complete the statements describing the relationships between the three side lengths that form a triangle. Use less than, equal to, or greater than.
The sum of the lengths of the two shorter sides is ____________ the length of the longest side.
Answer:
The sum of the lengths of the two shorter sides is greater the length of the longest side.
F. Complete the summary of what you have discovered so far for three segments with lengths a, b, and c, where c is the greatest length.
If a + b is equal to or ______________ than c, the segments cannot form a triangle. If a + b is ______________ than c, the segments form one triangle.
Answer:
If a + b is equal to or greater than c, the segments cannot form a triangle. If a + b is less than c, the segments form one triangle.
Question 3.
Can you draw a quadrilateral with side lengths of 2, 3, 4, and 5 units?
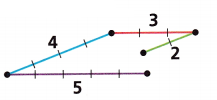
A. Make and use a model. Can you connect the endpoints to form a quadrilateral? If so, draw a quadrilateral. If not, explain why you cannot.
Answer:
Yes, we can draw quadrilateral.
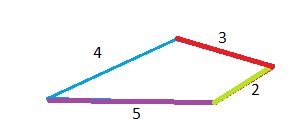
Explanation:
Connect all the end points of a given picture, the result is quadrilateral.
A quadrilateral is a polygon with four sides, four vertex and four angles.
B. Using the same side lengths, can you make a quadrilateral that is different than the one you drew in Part A? If so, draw it. If not, explain why you cannot.
Answer:
A quadrilateral can also have the same lengths of sides.
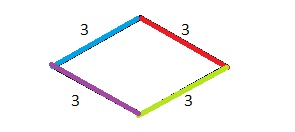
Explanation:
Yes, we draw a quadrilateral using the length of one side as shown above.
C. Make a conjecture about the number of quadrilaterals that can be made using four different segment lengths. Support your conclusion.
Answer:
Explanation:
The Quadrilateral Sum Conjecture tells us the sum of the angles in any convex quadrilateral is 360 degrees.
A polygon is convex if each of its interior angles is less that 180 degree.
Turn and talk Is it possible that four segments cannot form a quadrilateral?
Answer:
Yes, it forms a quadrilateral.
Explanation:
A quadrilateral is formed by four line segments that intersect at their endpoints.

Step It Out
Question 4.
In Parts A-C, let a and b be the shorter lengths and c be the longest length. Compare a + b to c to determine if a triangle can be made. Write <, =, or >.
A. Nia wants to make a triangular picture frame from strips of wood that are 9 centimeters, 11 centimeters, and 15 centimeters long.
9 + 11 ![]() 15
15
Since the sum of the lengths of two shorter strips is ____________ the length of the longest strip, Nia (can / cannot) make a triangle.
Answer:
9 + 11 > 15
Explanation:
Since the sum of the lengths of two shorter strips is greater than the length of the longest strip, Nia can make a triangle.
B. Gerard has pieces of string 6 inches, 5 inches, and 11 inches in length that he plans to use as a border for a collage.
6 + 5 ![]() 11
11
Since the sum of the lengths of two shorter pieces is ___________ the length of the longest piece, Gerard (can / cannot) make a triangle.
Answer:
6 + 5 > 11
Explanation:
Since the sum of the lengths of two shorter pieces is greater then the length of the longest piece, Gerard can make a triangle.
C. Olivia gives her niece leftover pieces of ribbon from her art supplies. They are 12 inches, 10 inches, and 24 inches long.
12 + 10 ![]() 24
24
Since the sum of the lengths of two shorter pieces of ribbon is ____________ the length of the longest, Olivia’s niece (can / cannot) make a triangle.

Answer:
12 + 10 < 24
Explanation:
Since the sum of the lengths of two shorter pieces of ribbon is less than the length of the longest, Olivia’s niece cannot make a triangle.
D. Amil is making a bamboo picture frame. Given the side lengths shown for the first two sides, what is one possible side length that will form a triangular picture frame?
5 + 8 = ___________, so one side length that will make a triangle is __________ inches.
Answer:
5 + 8 = 13, so one side length that will make a triangle is 12 inches.
Check Understanding
Question 1.
Max has three pieces of oak trim that are 7 inches, 11 inches, and 18 inches long. He wants to use them to make a triangular base for a candleholder. Will the pieces make a triangle? Explain your answer.
Answer:
No, pieces cannot make a triangle.
Explanation:
Since the sum of the lengths of two shorter pieces of oak trim is equal to the length of the longest, Max cannot make a triangle.
Question 2.
Bella is making a sculpture. She has pieces of copper pipe that are 4 centimeters long and 13 centimeters long. What is a possible third length of copper pipe that will make a triangle? Justify your answer.
Answer:
16 units
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
4 + 13 = 17 cm
the third side should be less then 17 cm
a possible third length of copper pipe that will make a triangle is 16 units
On Your Own
Question 3.
Horace is making a shadow box in the shape of a triangle to hold his homerun baseballs. He has pieces of wood 12 inches, 12 inches, and 26 inches long. Show whether these pieces will make a triangle.
Answer:
23 inches long
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
12 + 12 = 24 inches
the third side should be less then 24 inches
these pieces will not make a triangle because of the third side is 23 inches long.
Question 4.
Art An artist is going to make triangle earrings from glass rods with the lengths shown. Show whether these rods will make a triangle.

Answer:
Yes, rods will make triangle as shown below.
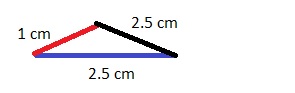
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
2.5 + 2.5 = 3 cm
Question 5.
Alan makes triangular potholders and sews edging around the outside. He has pieces of edging 5 inches, 5 inches, and 10 inches long. Show whether these pieces will make a triangle.
Answer:
No, we cannot make a triangle.
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
5 + 5 = 10 inches
the third side should be less then 10 inches
these pieces will not make a triangle
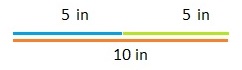
Question 6.
Open-Ended The volleyball team is making a triangular banner for their last home game. They want two of the sides to be 4 feet long each. Determine one possible length for the third side. Justify your answer.
Answer:
possible length for the third side is less then 8 ft
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
4 + 4 = 8 feet
the third side should be less then 8 ft
possible length for the third side is less then 8 ft
Question 7.
Reason Dante is constructing a quadrilateral with four sides, each 2 inches long. How many different quadrilaterals can he make? Explain.
Answer:
Dante can construct a quadrilateral with four sides, each 2 inches long known as square.
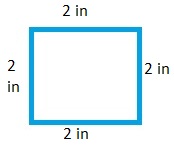
Explanation:
The sides of a square are all equal length, making it a regular quadrilateral.
All the angles in a square are right angles (90º).
Determine whether each set of numbers could be lengths of the sides of a triangle.
Question 8.
17, 13, 11 ____________
Answer:
yes, it can make a triangle.
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
13 + 11 = 24
24 > 17 triangle can form
Question 9.
11, 19, 35 ____________
Answer:
No, it cannot make a triangle.
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
11 + 19 = 30
30 < 35 triangle can not form
Question 10.
6, 7, 13 _____________
Answer:
No, it cannot make a triangle.
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
6 + 7 = 13
13 = 13
Two side lengths of a triangle are given. Find a possible third length.
Question 11.
5 meters, 12 meters
Answer:
possible third length is less then 17 meters
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
5 + 12 =17
5 meters, 12 meters are two side lengths of a triangle, a possible third length is less then 17m.
Question 12.
3 feet, 9 feet
Answer:
possible third length is less then 12 feet
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
3 + 9 =12 feet
3 feet, 9 feet are two side lengths of a triangle, a possible third length is less then 12 feet.
Question 13.
23 miles, 31 miles
Answer:
possible third length is less then 54 miles
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
23 + 31 =54
23 miles, 31 miles are two side lengths of a triangle, possible third length is less then 54miles.
Question 14.
A craftsman makes stained glass crafts. He has metal strips of lengths 5 inches, 8 inches, and 11 inches. Show whether these strips will make a triangle.

Answer:
yes, strips make a triangle.
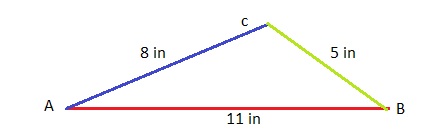
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
8 + 5 = 13 in
13 > 11 So, triangle can form.
Question 15.
Karissa is building a triangular landscape border around her mailbox. She has logs 4 feet, 5 feet, and 10 feet long. Show whether these logs will make a triangle.
Answer:
No, triangle cannot form.
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
4 + 5 = 9
9 < 10 feet
triangle can not form, third log must be less then 9 ft
Question 16.
Pierce is developing his own board game. The border of the board is going to be 3 pieces of cardboard, each 17 inches long. Show whether these lengths will make a triangle.
Answer:
Yes, lengths will make a triangle.
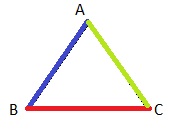
Explanation:
Length AB = BC = CA = 17 in
the board is going to be 3 pieces of cardboard, each 17 inches long
The sum of the length of the two sides of a triangle is greater than the length of the third side.
17 + 17 = 34 in
So, 34 > 17 make a triangle.
Question 17.
Construct Arguments Risa has four sticks measuring 2 inches, 2.5 inches, 3 inches, and 8 inches. She wants to connect the sticks end to end to make a quadrilateral. Can she do it? Explain why or why not.
Answer:
Yes, she can do it.
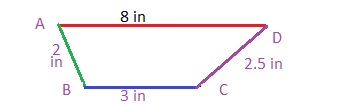
Explanation:
A quadrilateral has four side, four angles and 2 sides are parallel.
So, Risa can construct a quadrilateral.
Determine whether each set of numbers could be lengths of the sides of a triangle.
Question 18.
8.5, 6, 10 ___________
Answer:
yes, lengths form a triangle.
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
6 + 8.5 = 14.5
14.5 >10 triangle can be formed.
Yes, set of numbers could be lengths of the sides of a triangle
Question 19.
2.5, 2.5, 4 ____________
Answer:
Yes, lengths can form a triangle.
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
2.5 + 2.5 = 5
5 > 4 triangle can be formed.
Yes, set of numbers could be lengths of the sides of a triangle
Question 20.
5, 12, 18 ___________
Answer:
No, lengths cannot form a triangle.
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
5 + 12 = 17
17 < 18 triangle can not be formed.
No, set of numbers could not be lengths of the sides of a triangle.
Two side lengths of a triangle are given. Find a possible third length.
Question 21.
5 inches, 10 inches
Answer:
Possible length of third side is less then 15 inches.
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
5 + 10 = 15 inches
the third side should be less then 15 in
possible length for the third side is less then 15 in
Question 22.
6 yards, 18 yards
Answer:
Possible length of third side is less then 24 yards.
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
6 + 18 = 24 yards
So, the possible length of third side should be less then 24 yards.
Question 23.
9 meters, 21 meters
Answer:
Possible length of third side is less then 30 meters.
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
9 + 21 = 30 meters
So, the possible length of the third side should be less then 30 meters.
I’m in a Learning Mindset!
Did I find a different or unique way to determine whether a set of side lengths could form a triangle? What is it?
Answer:
Yes, we can find the length of third side in different way.
Explanation:
The sum of the length of the two sides of a triangle ABC of lengths a, b and c is greater than the length of the third side.
a + b = x units
So, the third side should be less then x units.
possible length for the third side c is less then x units.
Lesson 9.2 More Practice/Homework
Question 1.
Haley is making a triangle-shaped box garden. She has wooden pieces of lengths 6 feet, 8 feet, and 13 feet. Show whether these pieces will make a triangle.
Answer:
Yes, pieces will make a triangle.
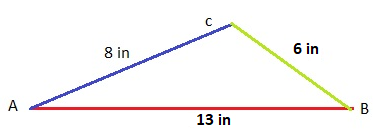
Explanation:
A triangle-shaped box garden has wooden pieces of lengths 6 feet, 8 feet, and 13 feet.
The sum of the length of the two sides of a triangle is greater than the length of the third side.
6 + 8 = 14 in
14 > 13 triangle can be formed.
Question 2.
Students are making shapes with string in an art class. Ben has pieces of string measuring 4 inches, 2 inches, and 1.5 inches long. Show whether these lengths will make a triangle.
Answer:
Yes, lengths will make a triangle.
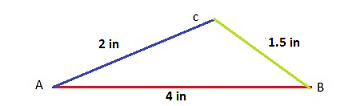
Explanation:
Ben has pieces of string measuring 4 inches, 2 inches, and 1.5 inches long and the lengths will make a triangle.
The sum of the length of the two sides of a triangle is greater than the length of the third side.
2 + 1.5 = 3.5 in
3.5 < 4 triangle can not form
Question 3.
Construct Arguments The Culinary Club is making a triangle-shaped sign showing a piece of pie for their pie-eating competition. Two of the sides measure as shown. Determine a possible length for the third side. Justify your answer.

Answer:
possible length for the third side is less then 6 feet
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
3 + 3 = 6 feet
So, the possible length of the third side should be less then 6 feet.
Question 4.
Seth wants to make a quadrilateral charm for a necklace. He has wire pieces with lengths 1 centimeter, 2 centimeters, 4 centimeters, and 5 centimeters. How many possible quadrilaterals are there with those side lengths?
Answer:
one quadrilateral
Explanation:
a quadrilateral charm for a necklace
Given lengths 1 centimeter, 2 centimeters, 4 centimeters, and 5 centimeters
possible quadrilaterals are there with those side lengths
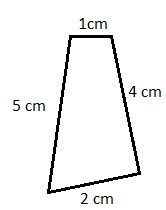
Determine whether each set of numbers could be lengths of the sides of a triangle.
Question 5.
2, 4, 6 _________
Answer:
No, length of the sides of a triangle is not possible.
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
2 + 4 = 6
6 = 6 So, triangle can not be formed.
Question 6.
16, 21, 33 __________
Answer:
Yes, length of the sides of a triangle is possible.
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
16 + 21 = 37
37 > 33
Yes, set of numbers could be lengths of the sides of a triangle.
Question 7.
1, 3, 3 ___________
Answer:
Yes, length of the sides of a triangle is possible.
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
1 + 3 = 4
4 > 3
Yes, set of numbers could be lengths of the sides of a triangle
Two side lengths of a triangle are given. Find a possible third length.
Question 8.
6 meters, 8 meters
Answer:
possible length for the third side is less then 14 meters.
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
6 + 8 = 14 meters
So, the third side should be less then 14 meters.
Question 9.
4 feet, 5 feet
Answer:
possible length for the third side is less then 9 feet.
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
4 + 5 = 9 feet
So, the third side should be less then 9 feet.
Question 10.
4.5 yards, 7 yards
Answer:
possible length for the third side is less then 11.5 yards.
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
4.5 + 7 = 11.5 yards
So, the third side should be less then 11.5 yards.
Test Prep
Question 11.
Lorelei is making decorative boxes in the shape of triangles. Which of the following could be the lengths of the sides of the boxes?
(A) 12 cm, 13 cm, 24 cm
(B) 12 cm, 13 cm, 25 cm
(C) 10 cm, 10 cm, 24 cm
(D) 10 cm, 10 cm, 22 cm
Answer:
Option (A)
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
12 + 13 = 25 cm
So, the third side should be less then 25 cm.
Question 12.
Lhu builds dollhouses with triangle-shaped roofs. Which of the following could be lengths of the edges of the roof of a dollhouse?
(A) 10 in., 10 in., 20 in.
(B) 10 in., 12 in., 24 in,
(C) 11 in., 12 in., 24 in.
(D) 11 in., 11 in., 20 in.
Answer:
Option (D)
Explanation:
The sum of the length of the two edges of a triangle is greater than the length of the third edge 11 + 11 = 22 cm
So, the third side should be less then 22 cm.
lengths of the edges of the roof of a dollhouse are 11 in., 11 in., 20 in.
Question 13.
Select all the sets of numbers that could be lengths of the sides of a triangle.
(A) 2, 7, 9
(B) 4, 11, 13
(C) 6, 9, 12
(D) 6, 6, 14
(E) 8, 15, 21
(F) 9, 17, 27
Answer:
The following are the sets of numbers that could be lengths of the sides of a triangle.
(B) 4, 11, 13
C) 6, 9, 12
(E) 8, 15, 21
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
Question 14.
An artist gets strips of metal from a salvage yard to make decorative wall art. He finds strips that are 2.5 feet and 3.5 feet long. Determine one possible length for the third strip if the artist wants to make a triangle.
Answer:
possible length for the third side is less then 6 feet
Explanation:
The sum of the length of the two sides of a triangle is greater than the length of the third side.
2.5 + 3.5 = 6 feet
So, the third side should be less then 6 feet.
Spiral Review
Question 15.
Kevin wants to buy a video game for $45. He also wants to buy 2 game controllers. Each controller costs the same amount. He has a total of $120 to spend. Write and solve an inequality to find how much Kevin can spend on each controller. $37.5
Answer:
Kelvin spends $120
Explanation:
cost of a video game $45
cost of each game controller is same.
120 – 45 = $75
75/2 = $37.5
Kevin can spend on each controller = $37.5
37.5 +37.5 + 45 = $120
Question 16.
Sofia has 16 hours to paint a living room and 2 bedrooms. She spends 7 hours painting the living room. Write and solve an inequality to find how much time she can spend on each bedroom if she splits her time equally.
Answer:
4.5hours
Explanation:
Sofia has 16 hours to paint a living room and 2 bedrooms.
Sofia spends 7 hours painting the living room
16 – 7 = 9 hours to paint a living room and 2 bedrooms
9/2 = 4.5 hours can spend on each bedroom if she splits her time equally