We included HMH Into Math Grade 7 Answer Key PDF Module 9 Lesson 1 Draw Circles and Other Figures to make students experts in learning maths.
HMH Into Math Grade 7 Module 9 Lesson 1 Answer Key Draw Circles and Other Figures
I Can inscribe triangles in circles and draw geometric figures meeting given conditions.
Spark Your Learning
Parker plans to build a circular fire pit in a square area. He is drawing a model on paper to confirm his plans before he starts to build. How can Parker use paper folding and a compass to draw the largest possible circular fire pit in the space he has staked off? Trace Parker’s square to a piece of paper and draw the circle for the fire pit.

Answer:

Explanation :
Fold the paper into half and again fold the paper into half to make a square one-fourth.
Trace a curve from one side to another side of the circle using a compass.
cut out the curve from the folded paper and open the folds
we will get the largest
Turn and Talk Brainstorm a list of characteristics specific to squares and circles.
Answer:
Square
It has 4 sides
It has 4 corners
It is a 4 sided shape
Circle
It does not have sides
It does not have corners
Build Understanding
Question 1.
A polygon is inscribed in a circle if every vertex of the polygon is on the circle. To investigate the kinds of triangles that can be inscribed in a circle, begin Parts A and B by using a compass to draw a circle with a radius of 0.5 inch. The radius of a circle is the distance from the circle’s center to any point on the circle.
A. Draw a circle and inscribe a triangle in it. Inscribe more than one if you can.
Answer:
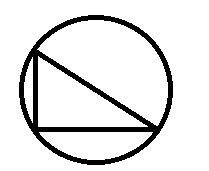
Explanation:
We can inscribe all the triangles like equilateral triangle, isosceles triangle and right angle triangle by drawing a circle with a radius of 0.5 inch and inscribe the triangle touching the vertex of every polygon in the circle.
B. Draw a circle and a diameter, which is a segment that passes through the circle’s center and has endpoints on the circle. Use the endpoints of the diameter and a third point on the circle to inscribe a triangle in the circle.
Answer:
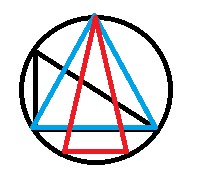
Explanation:
By Using the endpoints of the diameter and a third point on the circle we inscribe a triangle.
C. Draw three circles, each with a diameter of 1 inch. Can you inscribe each triangle in one of the circles? If so, draw it. If not, justify your answer.
a triangle with a 50° angle
a triangle with a side of length 1.25 inches
a triangle with a 30° and a 60° angle
Answer:
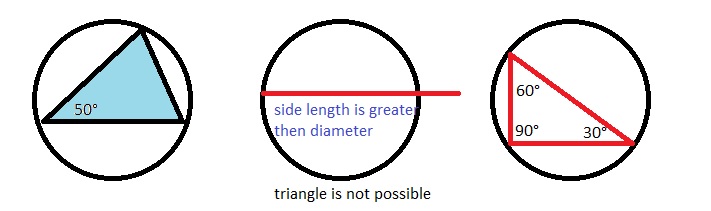
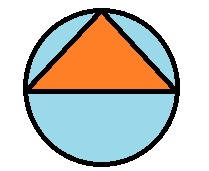
Explanation:
By using the given information a triangle with a side of length 1.25 inches is not possible , because of the diameter is of 1 inch and the side length is 1.25in.
So, when we draw the triangle comes out of the circle.
Turn and Talk How many triangles can you draw in each of Parts A through C: none, only one, or more than one?
Answer:
More than one.

Step It Out
Question 2.
Draw a hexagon with side lengths 2, 3, 4, 5, 6, and 7 units. The two longest sides are perpendicular. The longest side and the third-longest side are parallel.
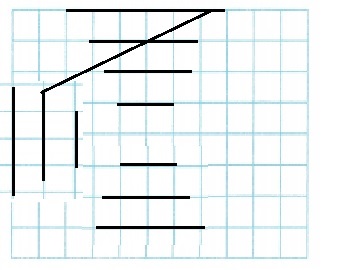
A. Begin by drawing the two longest sides perpendicular to each other. How can you draw two perpendicular segments?

Answer:
Explanation:
As, shown above the two longest sides are perpendicular.
The longest side and the third-longest side are parallel.
B. Draw the third-longest side parallel to the longest side and connected to the second-longest side. How can you draw two parallel segments?
Answer:
Explanation:
As, shown above the third-longest side is parallel to the longest side and connected to the second-longest side.
C. Use a ruler or compass to draw the last three segments, or cut thin strips of paper. Use the segments to complete the hexagon.
The figure (does / does not) have at least one line of symmetry.
Answer:

Explanation:
Above hexagon shows the line of symmetry.
Question 3.
Kaylee has a square piece of wood with a side length of 48 inches. She wants to use it to build the largest circular tabletop that she can.
A. Draw a scale model of the piece of wood. Be sure to include the scale used in your model. Then draw the diagonals to find the center of the square, which will also be the center of the circle, and draw the circle.
Answer:
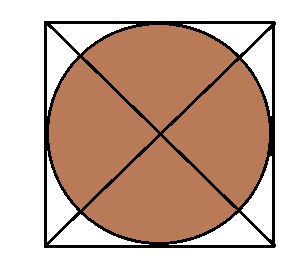
B. What is the diameter of the circle in the model? What is the diameter of the tabletop? How do you know?
Answer:
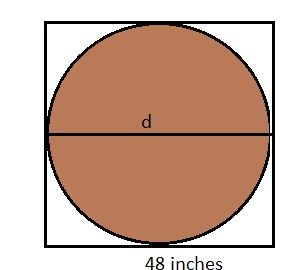
the diameter of the the table top is 48 inches
Check Understanding
Question 1.
Draw a circle. Can you inscribe an obtuse triangle? If so, inscribe an obtuse triangle and tell how many you can draw. If not, explain why not.
Answer:
Yes, Obtuse triangle in a circle.
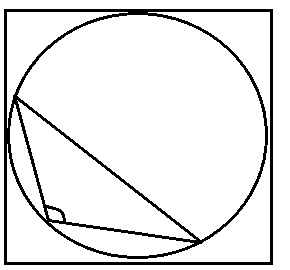
Explanation:
A triangle inside the circle will be obtuse if and only if its three vertices lie on one side of a diameter of the circle.
Question 2.
Use tools to draw a hexagon in which exactly three sides have a length of 3 units and there are two pairs of parallel sides.

Answer:
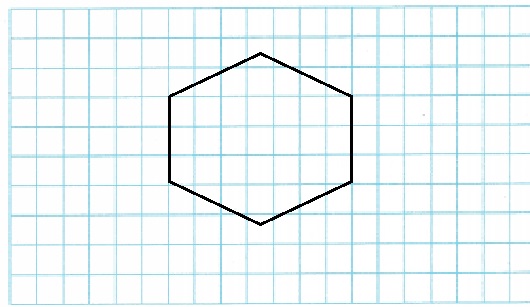
Explanation:
Above figure shows exactly three sides which have a length of 3 units and two pairs of parallel sides.
Question 3.
A square has a side length of 2.5 meters. What is the radius of the largest circle that fits inside the square?
Answer:
Radius = 1.25 m
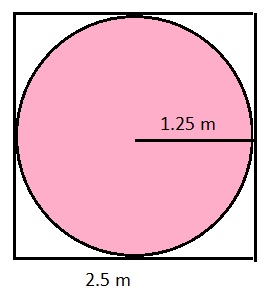
Explanation:
A square has a side length of 2.5 meters. the diameter of of a circle insert in the square is 2.5m. The radius of the largest circle that fits inside the square is
r = d/2
d = 2.5 m
r = 2.5/2
r = 1.25 m
On Your Own
Question 4.
Use Tools Draw an octagon with six sides of length 3 units, one side of length 4 units, and one side of length 10 units. Every pair of sides that meet are perpendicular. The figure should have symmetry.

Answer:
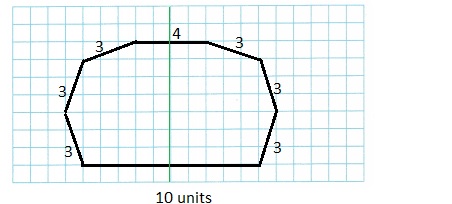
Explanation:
As, shown above every pair of side meet perpendicular to each other with symmetry.
Question 5.
Use Tools Draw a quadrilateral with two pairs of opposite sides that are parallel and equal in length, no right angles, and no lines of symmetry. What is the quadrilateral?
Answer:
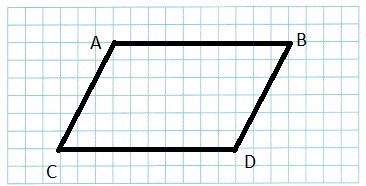
Explanation:
As, shown above the quadrilateral no right angles and lines of symmetry.
It has only two pairs of opposite sides that are parallel and equal in length.
Question 6.
Use Tools Draw a circle and one of its diameters. Can you inscribe a triangle that has the diameter as a side and includes an obtuse angle? If so, draw the triangle. If not, justify your answer.
Answer:
Yes, we can draw a obtuse triangle.
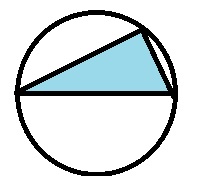
Explanation:
An obtuse angle is greater than 90 degrees,
half of the circle is 180 degrees.
So, we can inscribe an obtuse triangle in a circle.
Question 7.
Open-Ended Draw an octagon with seven sides of length 4 units and one side of length 12 units. The longest side should be perpendicular to at least two of the shorter sides and parallel to at least two of the shorter sides.
Answer:
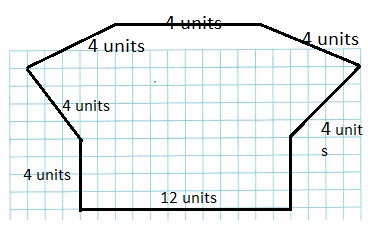
Explanation:
A polygon octagon ahs 8 sides, we take base as 12 units and the rest of the sides as 7 units.
As, shown above the longest side is perpendicular to the shorter sides and also parallel.
Question 8.
Use Tools Draw a quadrilateral with exactly one pair of parallel sides. What is the quadrilateral?

Answer:
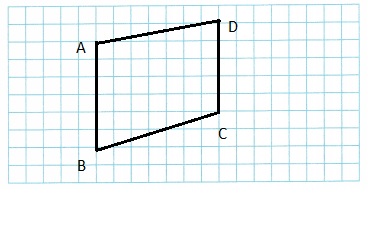
Explanation:
A quadrilateral has four sides parallel to each other and four angles.
As, shown above one side of the quadrilateral is parallel to each other.
Question 9.
Marcel made a pot pie and shared it with his friends. Draw a circle graph to show the portion eaten by each person. The measure of the angle between the sides of the section for each friend is given.
Marcel: 90° Jake: 135° Tasha: 90° Elisa: 45°
Answer:
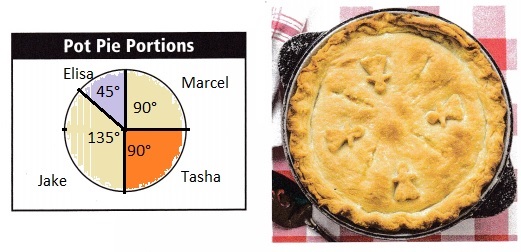
Explanation:
The above figure shows a circle graph portion eaten by each person.
The measure of the angle between the sides of the section for each friends are marked as,
Marcel: 90° Jake: 135° Tasha: 90° Elisa: 45°
I’m in a Learning Mindset!
What can I apply from my knowledge of circles to better understand circle graphs?
Answer:
A circle is a complete angle with 360° with respect center.
pictorial representation of data using circle is so effective.
Lesson 9.1 More Practice/Homework
Question 1.
Use Tools Draw a decagon with eight sides of length 2 units and two sides of length 4 units. Any two sides that meet should be perpendicular, and the figure should contain parallel segments.

Answer:
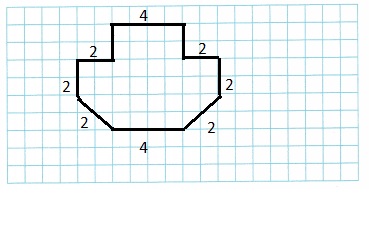
Explanation:
As, shown above draw a decagon with 8 sides of length 2 units and two sides of length 4 units. Two sides that meet should be perpendicular, and the figure should contain parallel segments.
Question 2.
Use Tools Draw a quadrilateral with two pairs of congruent sides, no parallel sides, and one line of symmetry. What is the quadrilateral?

Answer:
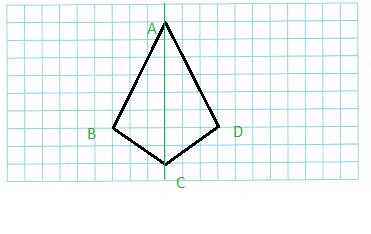
Explanation:
Rhombus a quadrilateral with two pairs of congruent sides, no parallel sides, and one green line of symmetry is drawn.
A kite is a quadrilateral with exactly two pairs of adjacent congruent sides.
Question 3.
Use Tools Draw a circle with a radius of \(\frac{3}{4}\) inch and a horizontal diameter. Inscribe a triangle that has the diameter as a side and a vertical line of symmetry.
Answer:
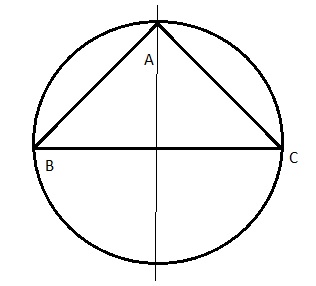
Explanation:
A circle with a radius of \(\frac{3}{4}\) inch and a horizontal diameter.
Inscribe a triangle that has the diameter as a side and a vertical line of symmetry.
Test Prep
Question 4.
Match each figure with its description.

Answer:
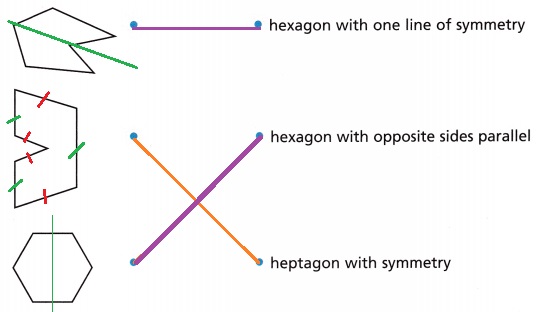
Explanation:
Green line is for showing the line of symmetry for first and last picture,
where as middle picture contains parallel lines.
Question 5.
A. Use tools to draw a quadrilateral with four sides of length 3 units, two pairs of parallel sides, and four lines of symmetry. What is the quadrilateral?
Answer:

Explanation:
As shown above Quadrilateral has 4 equal sides with 3 units each.
B. What is the radius of the largest circle that fits inside your quadrilateral from Part A?
Answer:
1.5 units
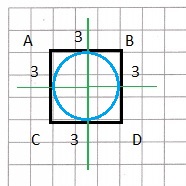
Explanation:
As shown above Quadrilateral has 4 equal sides with 3 units each.
Joining all the sides draw a circle with diameter 3 units and radius
d = 2r
r = d/2
r = 3/2 = 1.5
Spiral Review
Question 6.
Betty is 5 more than 3 times Jadyn’s age. Betty is 41 years old. Write and solve an equation to find Jadyn’s age.
Answer:
12 years
Explanation:
Let Jadyn’s age is x
Betty is 5 more than 3 times Jadyn’s age
B = 3x + 5
B = 41
41 = 3x + 5
41 – 5 = 3x
3x = 36
x = 12
Jadyn’s age is 12 years
Question 7.
Angles 1 and 2 are complementary. The measure of Angle 2 is two times the measure of Angle 1. Write and solve an equation to find the measure of both angles.
Answer:
Measure of both the angles is 90 degrees.
Explanation:
Two angles are said to be complementary angles if they add up to 90 degrees.
In other words, when complementary angles are put together, they form a right angle.
Angle 2 = 2 Angle 1
Angle 1+ Angle 2 = 90°
Angle 1 + 2 x Angle 1 = 90°
3 x Angle 1 = 90°
Angle 1 = 30°
Angle 2 = 2 x Angle 1 = 60°