We included HMH Into Math Grade 7 Answer Key PDF Module 8 Lesson 1 Understand and Apply Properties to Solve One-Step Inequalities to make students experts in learning maths.
HMH Into Math Grade 7 Module 8 Lesson 1 Answer Key Understand and Apply Properties to Solve One-Step Inequalities
I Can solve one-step inequalities by applying properties and graph the solutions on a number line.
Spark Your Learning
Suppose the lowest elevation to which the submarine shown has been tested is -490 meters. If it is currently at an elevation of -125 meters, how many meters more can it dive without going below the lowest elevation tested?

Answer:
– 365 meters
Explanation:
The lowest elevation to which the submarine shown has been tested is -490 meters.
If it is currently at an elevation of -125 meters,
Number of meters more can it dive without going below the lowest elevation tested
– 490 – (-125) = – 365 meters
Turn and Talk Can the submarine dive 200 meters more without going below the lowest elevation tested? 400 meters more? How do you know?
Answer:
200 meters more : YES
400 meters more : NO
Explanation :
Lowest elevation tested = -490
Elevation of submarine = -125
if it goes 200 meters more
-125 + ( -200 ) = -325
-325 > -490
so the submarine can go 200 meters more without going below the lowest elevation tested
if it goes 400 meters more
-125 + ( -400 ) = -525
-525 < -490
so the submarine can not go 400 meters more without going below the lowest elevation tested
Build Understanding
Recall that an equation is a mathematical sentence showing that two quantities are equal, or equivalent. Likewise, an inequality is a mathematical sentence showing that two quantities are not equivalent. The meanings of inequality symbols are shown in the table.
Connect to Vocabulary
The solution of an inequality is a value or values that makes an inequality true.

The number line shows x = 365. Note the closed circle represents “or equal to” in the inequality to indicate the inclusion of 365.

Question 1.
A submarine is at sea level, and it descends with a rate of change of -10 feet per second.
A. Write an inequality to represent the time t it takes the submarine to reach an elevation of -140 feet or deeper.
Answer:
14 min
Explanation:
rate of change of -10 feet per second.
time t it takes the submarine to reach an elevation of -140 feet or deeper.
-10 t < -140
t <= 140 /10
t <= 14
B. Write three values for t that will make the inequality from Part A true. Substitute each value in the inequality to check. Then describe the set of numbers that can make the inequality true.
Answer:
– 160 < -140
Explanation:
rate of change of -10 feet per second.
time t it takes the submarine to reach an elevation of -140 feet or deeper.
-10 t ≤ -140
t=14 -10(14) < -140
t=15 -10(15) < -140
-150 < -140
t=16 – 10(16) < -140
– 160 < -140
C. Solve the inequality from Part A by writing a simple inequality that describes all of the numbers that will make the inequality true. Write an inequality symbol in the first box and a number in the second box.
![]()
Answer:

Explanation:
rate of change of -10 feet per second.
time t it takes the submarine to reach an elevation of -140 feet or deeper.
-10 t < -140
t ≤ 140 /10
t ≤ 14
D. Graph the inequality from Part C. Can the submarine reach an elevation of -140 feet or deeper in less than 14 seconds?

Answer:
No, the submarine cannot reach an elevation.

least amount of time is t = 14 seconds
Explanation:
rate of change of -10 feet per second.
time t it takes the submarine to reach an elevation of -140 feet or deeper.
-10 t < -140
t ≤ 140 /10
t ≤ 14
E. How are solving -10t = -140 and -10t = -140 alike? How are they different?
Answer:
Solving -10t = -140 and -10t = -140 alike
Explanation:
-10t = -140 and -10t = -140 alike
t = 14 and t = 14 alike
Step It Out
Question 2.
During the spring rains, the water level in a lake rises. Although the lake has a dam, when the water reaches the top of the dam, water will begin flowing over the top.
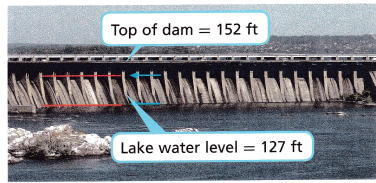
A. Write an inequality that expresses how much more the lake can rise r so that the water does not flow over the top of the dam.
Answer:
25 seconds
Explanation:
water level in lake is 127ft, top of dam is 152ft
raise of water level is represented as r.
127 + r ≤ 152
r ≤ 152 – 127
r ≤ 25
B. Write three values for r that will make the inequality from Part A true. Then write and graph a simple inequality that describes all of the numbers that will make the inequality true.
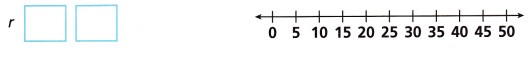
Answer:

Explanation:
water level in lake is 127ft, top of dam is 152ft
raise of water level is represented as r.
r ≤ 25
127 + r ≤ 152
r ≤ 25
Turn and Talk How are solving 127 + r = 152 and solving 127 + r = 152 alike, and how are they different?
Answer:
Solving 127 + r = 152 and solving 127 + r = 152 alike
Explanation:
water level in lake is 127ft, top of dam is 152ft
raise of water level is represented as r.
127 + r = 152 and solving 127 + r = 152 alike
r = 152 – 127 and r = 152 -127
r =25 and r = 25
The properties of equality used when solving equations hold true for a inequalities, with one exception. When you multiply or divide by a negative number, you must reverse the inequality symbol.
Question 3.
Apply properties of inequalities to solve each inequality.
A.
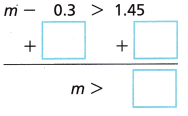
Answer:

B.
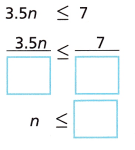
Answer:

C.
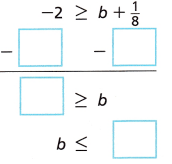
Answer:
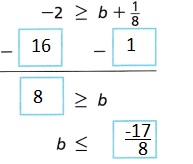
D.
Answer:

E.
Answer:
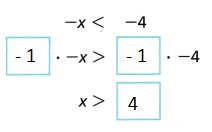
F.
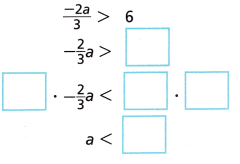
Answer:
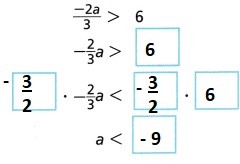
Question 4.
Leila is designing a rectangular table. What is the range of values for x if the area of the table shown is to be 12 square feet or less?
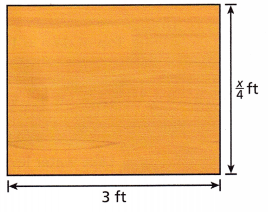
A. What is the inequality using the formula for the area of a rectangle?
Answer:
12 ≤ 3 x \(\frac{x}{4}\)
Explanation:
The range of values for x if the area of the table shown is to be 12 square feet or less.
Area of a rectangle A = length x width = 12 sq feet
12 ≤ 3 x \(\frac{x}{4}\)
B. Solve the inequality for x.
Answer:
x ≤ 16
Explanation:
3 x \(\frac{x}{4}\) ≤ 12
\(\frac{3x}{4}\) ≤ 12
x ≤16
\(\frac{12 x 4}{3}\) = x
x ≤ 16
C. Give the range of values for x that are reasonable in the context of this problem. Graph the solution.

Answer:

Explanation:
x ≤ 16
An inequality compares two values, showing if one is less than, greater than,
or simply not equal to another value.
Turn and Talk What is the longest the unknown side of the table can be? Explain.
Answer:
The longest side must be diagonal of the table.
Explanation:
since if we bisect the rectangle into 2 halves, we get 2 right angle triangles.
since the hypotenuse is the longest side of triangle the diagonal is same as the hypotenuse.
hence the diagonal is the longest side of a given table of unknown side.
Check Understanding
Question 1.
The veterinarian told Hector that his 8-inch puppy would get no taller than 24 inches. Write and solve an inequality to find how much more his puppy, shown here, may grow.

Answer:
8x > 24
Explanation:
x > 3 inch
write the factors of 3 for 8 time.
x = 3 , 6 , 9 , 12 , 15 , 18 , 21 , 24 inches
So, 8x > 24
For Problems 2-3, solve the inequality. Graph the solution.
Question 2
–\(\frac{2x}{3}\) = 2
![]()
Answer:
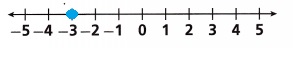
Explanation :
–\(\frac{2x}{3}\) = 2
– 2x = 2 x 3
– x = 6 ÷ 2
x = -3
Question 3.
x – 2 > -6
![]()
Answer:
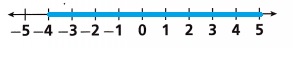
Explanation :
x > -6 +2
x > -4
On Your Own
For Problems 4-5, use the given information:
Harun is designing a room addition for a home and wants a rectangular window with area that is more than 12 square feet but not more than 24 square feet. Harun knows he wants the window to be 4 feet wide.

Question 4.
Model with Mathematics Write and solve an inequality to find the length x that will guarantee that the window is not too small. Explain.
Answer:
24 < 4x > 12
Explanation:
Harun knows he wants the window to be 4 feet wide.
Area of window = length x width
A = (x) x 4
a rectangular window with area that is more than 12 square feet but not more than 24 square feet.
4x is are of the rectangular window
24 < 4x > 12
Question 5.
Model with Mathematics Write and solve an inequality to find the length x that will guarantee that the window is not too large. Explain.
Answer:
24 < 20 > 12
Explanation:
let the length x = 5 feet
24 < 4x > 12
length x = 5 for a rectangular window
24 < 4 x 5 > 12
24 < 20 > 12
Question 6.
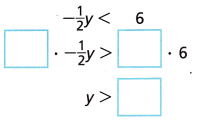
Use Structure Emir is solving the inequality –\(\frac{2}{3}\)x < 18. What steps should he follow to find the solution?
Answer:
x < 27
Explanation:
By multiplying –\(\frac{3}{2}\) on both the sides of the given equation as shown below
–\(\frac{2}{3}\)x < 18
=(-\(\frac{3}{2}\) )(-\(\frac{2}{3}\)) x <\(\frac{3}{2}\) 18
x < 27
For Problems 7-10, solve the inequality. Graph the solution.
Question 7.
10 ≤ x + 7 ____________

Answer:

Explanation:
10 ≤ x + 7
10 – 7 ≤ x
3 ≤ x
Question 8.
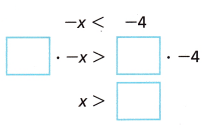
-x ≥ -5 _____________

Answer:

Explanation:
-x ≥ -5
x ≥ 5
Question 9.
\(\frac{3x}{5}\) > -6 ____________
![]()
Answer:
x > -10
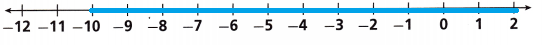
Explanation:
\(\frac{3x}{5}\) > -6
x > -6 x \(\frac{5}{3}\)
x >- \(\frac{30}{3}\)
x > -10
Question 10.
2 < –\(\frac{x}{3}\) ______________
![]()
Answer:
x > -6
![]()
Explanation:
2 < –\(\frac{x}{3}\)
– 3 x 2 < –\(\frac{x}{3}\) x -3
-6 < x
x > -6
For Problems 11-13, use the given information:
Three friends are shopping at the garage sale shown.

Question 11.
Attend to Precision Ming has $24. Write and solve an inequality for the number of shorts she can buy. Interpret the solution in the context of the problem.
Answer:
6 x ≤ 24
Explanation:
each shirt $6
Ming has $24
6x ≤ 24
x = 4
Ming can buy 4 shirts
Question 12.
Attend to Precision Camille can buy up to 5 shirts. How much money could she have?
Answer:
$30
Explanation:
cost of each shirt $6
Camille can buy up to 5 shirts
6 x 5 = 30
Question 13.
Construct Arguments Juanita has $24. Can she buy 5 shirts? Explain your answer.
Answer:
Juanita can not buy 5 shirts as she has $24 only
Explanation:
Juanita has $24. Can she buy 5 shirts
each shirt $6
Juanita can not buy 5 shirts as she has $24 only
6 x 5 = 30
Question 14.
Model with Mathematics Rudo has a target of at least $150 in pledges for a walkathon. He currently has $65 in pledges. Write and solve an inequality for the amount p Rudo has left to raise.
Answer:
p > 85
Explanation:
Rudo has a target of at least $150 in pledges for a walkathon.
He currently has $65 in pledges.
p > 150 – 65
p > 85
For Problems 15-17, solve the inequality. Graph the solution.
Question 15.
x – 2.5 > 8.7 _________
![]()
Answer:
x > 11.2

Explanation:
x – 2.5 > 8.7
x > 8.7 + 2.5
x > 11.2
Question 16.
1.8x ≤ 13.5 ___________
![]()
Answer:
x ≤ 7.5
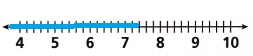
Explanation:
1.8x ≤ 13.5
x ≤ 13.5 /1.8
x ≤ 7.5
Question 17.
x + 1\(\frac{3}{5}\) < -2 _____________
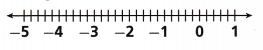
Answer:
x <- 3.6
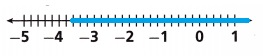
x + 1\(\frac{3}{5}\) < -2
x + \(\frac{8}{5}\) < -2
x < -2 – \(\frac{8}{5}\)
x < – \(\frac{10 + 8}{5}\)
x <- 3.6
I’m in a Learning Mindset!
What part of solving one-step inequalities elicits a fixed-mindset voice in my head?
Answer:
Part of solving one-step inequalities elicits a fixed-mindset voice in my head is
one unknown is >, < or = comparison
Lesson 8.1 More Practice/Homework
Question 1.
Model with Mathematics Cara is designing the rectangular patio shown. She wants the area of the patio to be larger than 72 square feet but no greater than 156 square feet.
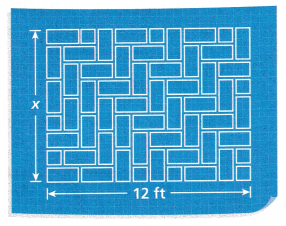
A. Write and solve an inequality representing a length that meets the requirement for the minimum area.
Answer:
L = 6ft.
Explanation :
Minimum Area = 72
length = l
breadth = 12
Area = length x breadth
Area = L x 12
72 = L x 12
L = 72 ÷ 12
L = 6ft.
B. Write and solve an inequality representing a length that meets the requirement for the maximum area.
Answer:
L = 13ft.
Explanation :
Minimum Area = 156
length = L
breadth = 12
Area = length x breadth
Area = L x 12
156 = L x 12
L = 156 ÷ 12
L = 13ft.
C. Describe the possible lengths for the unknown side.
Answer:
7ft , 8ft , 9ft , 10f , 11ft ,12ft
Explanation :
Area of the patio is larger than 72 square feet but no greater than 156 square feet.
let area be A
72 < A < 156
but A = length x breadth
A = X x 12 = 12x
72 < 12x < 156
solving both inequalities we get
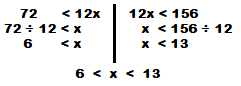
6 < x < 13
Question 2.
Math on the Spot Solve the inequality. Graph the solution.
A. -4x < 12 ____________
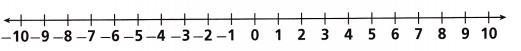
Answer:
x < -3

Explanation:
-4x < 12
x < – 12/4
x < – 3
B. -1 ≥ \(\frac{-w}{4}\) ____________
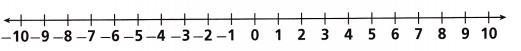
Answer:
-4 ≥ w

Explanation:
-1 ≥ \(\frac{-w}{4}\)
-4 ≥ w
Question 3.
STEM In the science lab, Will is testing the freezing point of a substance, which should be -24 °C. He is changing the temperature at a rate of -3 °C per minute, starting at 0 °C. Write and solve an inequality for the time t before the temperature reaches the freezing point.
Answer:
t ≥ -24 ÷ -3
t ≥ 8 minutes
Explanation :
Let time taken for the substance to reaches freezing point be ‘t’
final temperature = -24
Rate of change in temperature =-3
t ≥ final temperature ÷ rate of change in temperature
t ≥ -24 ÷ -3
t ≥ 8 minutes
Question 4.
Model with Mathematics Tania has already saved $25.75. She needs at least $53.88 to buy a set of headphones. Write and solve an inequality that shows how much more she needs to earn to buy headphones.
Answer:
Amount Tania needs to earn ≥ $53.88 – $25.75
Amount Tania needs to earn ≥ $28.13
Explanation :
Amount Tania has already saved = $25.75.
Amount Tania needs at least = $53.88
Amount Tania needs to earn ≥ Amount Tania needs at least – Amount Tania has already saved
Amount Tania needs to earn ≥ $53.88 – $25.75
Amount Tania needs to earn ≥ $28.13
Test Prep
Question 5.
Chan is in a running club and needs to run at least 500 miles in a year to earn the gold level of achievement. He is presently at 220 miles. Which inequality can be used to determine the additional number of miles he can run and earn gold?
(A) x + 220 < 500
(B) x + 220 ≥ 500
(C) x + 500 > 220
(D) x + 500 ≤ 220
Answer:
Option (B)
Explanation:
Chan is in a running club and needs to run at least 500 miles in a year to earn the gold level of achievement.
He is presently at 220 miles
x + 220 ≥ 500
Question 6.
Select the number line that represents the solution of the inequality 7 – x ≥ 4.

Answer:
Option(C)
Explanation:
The inequality equation 7 – x ≥ 4.
7 – x ≥ 4.
– x ≥ 4 -7
– x ≥ -3
x ≥ 3
Question 7.
Shawna earns $12.75 per hour. How many hours does she need to work to earn $102 or more?
at least / at most / less than / more than ____________ hours
Answer:
more than 8 hours
Explanation:
12.75 x ≥ 102
x ≥ 8
Spiral Review
Question 8.
Francisco bought 2 tickets online. The total charge was $35 with an online booking charge of $5. Use x to represent the price of a ticket. Write an equation that could be used to find the price of a ticket.
Answer:
P = $15
Explanation :
Total Price of 2 tickets = $35
Online booking charge = $5
Original price of 2 tickets = 35 – 5 = $30
Let Price of one ticket = P
P = 30 ÷ 2
P = $15
Question 9.
Solve for x.
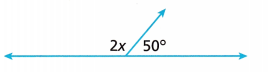
Answer:
x = 75
Explanation:
2x + 50 = 180
2x = 180 – 50
2x = 130
x = 130/2
x = 75
Question 10.
The perimeter of the table shown is 16 feet. Write an equation in the form px + q = r to solve for x.
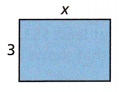
Answer:
x = 5
Explanation:
px + q = r
P = 2[3 + x]
P = 6 + 2x
16 = 6 + 2x
2x = 16 -6
2x = 10
x = 10/2
x = 5