We included HMH Into Math Grade 7 Answer Key PDF Module 6 Lesson 1 Apply Properties and Strategies to Operate with Rational Numbers to make students experts in learning maths.
HMH Into Math Grade 7 Module 6 Lesson 1 Answer Key Apply Properties and Strategies to Operate with Rational Numbers
I Can write and evaluate expressions involving rational numbers and name the properties used.
Step It Out
1. Remember that the properties of operations you used for integers, such as the Commutative and Associative Properties, the Inverse and Identity Properties, and the Distributive Property, can all be used for any rational numbers.

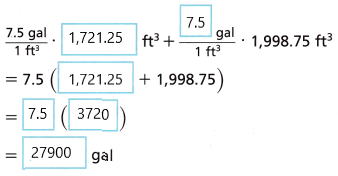
Stefan has 5 ounces of chlorine, and he needs to find out whether that is enough chlorine for two swimming pools. The amount of chlorine per gallon that Stefan will add is shown. One pool has volume 1,721.25 cubic feet, and the other has volume 1,998.75 cubic feet. There are about 7.5 gallons per cubic foot.
A. Write and evaluate an expression for the number of gallons in both pools.
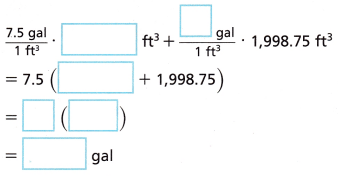
Answer:
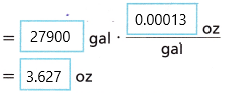
B. Write and evaluate an expression for the number of ounces of chlorine needed in both pools.
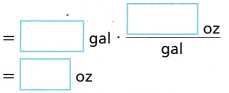
Answer:
Turn and Talk Which property of operations did you use in Part A above? Explain.
Answer:
The property of operations did you use in Part A above is Associative property.
a+(b+c)=(a+b)+c
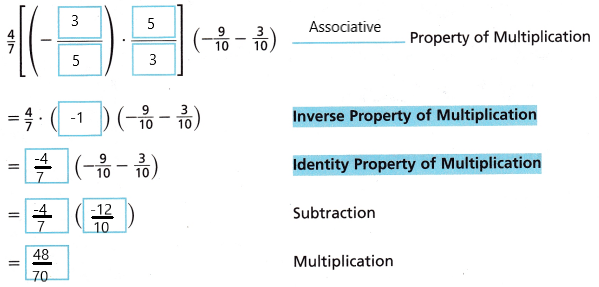
2. Use properties to evaluate \(\frac{4}{7}\)(-\(\frac{3}{5}\)) ∙ \(\frac{5}{3}\)(-\(\frac{9}{10}\) – \(\frac{3}{10}\))
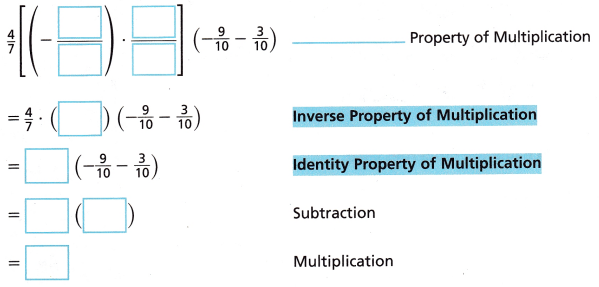
Answer:
3. A model car club has 6 ounces of white paint. They give \(\frac{1}{3}\) of the paint to a craft club. The amount of paint to use on each car is shown. Write and evaluate an expression to find the number of cars they can paint. Use the order of operations.
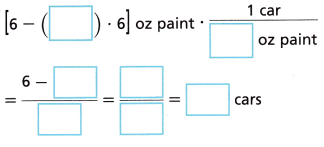

Answer:
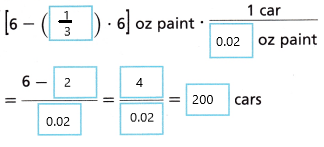
Check Understanding
Question 1.
Sarah buys 8 packages, each with 20 balloons, and uses \(\frac{1}{4}\) of them to decorate the hall. Write and evaluate an expression to find how many balloons Sarah has left.
Answer:
There are 40 ballons sarah has left.
Explanation:
From the given question find
(8 × 20) ÷ 4
160 ÷ 4
40
Question 2.
Suresh has 4 coupon books, each with 6 coupons. He keeps \(\frac{1}{3}\) of the coupons and gives the rest away. Fifty percent of those he keeps are for the movie theater. Write and evaluate an expression to show how many movie theater coupons he has.
Answer:
4 × 6 × \(\frac{1}{3}\) × \(\frac{1}{2}\)
4 coupons
Explanation:
Suresh owns 4 × 6 coupons that is 24 coupons.
He keeps \(\frac{1}{3}\) of the coupons.
So 4 × 6 × \(\frac{1}{3}\) = 8 coupons
Fifty percent of those he keeps are for the movie theater
4 × 6 × \(\frac{1}{3}\) × \(\frac{1}{2}\)
4 coupons
Question 3.
Explain how to use the properties to evaluate the expression mentally.
–\(\frac{3}{21}\) ∙ \(\frac{3}{5}\) ∙ 7 ∙ 15
Answer:
-9
Explanation:
Let us solve the given expression
The expression is –\(\frac{3}{21}\) ∙ \(\frac{3}{5}\) ∙ 7 ∙ 15
–\(\frac{3}{21}\) × \(\frac{3}{5}\) × 7 × 15
–\(\frac{1}{7}\) × \(\frac{3}{5}\) × 7 × 15
–\(\frac{3}{5}\) × 15
-9
On Your Own
Question 4.
Model with Mathematics Liu Tse is 6 years older than four times the age of her daughter, Lan. Lan will be 9 years old in 3 years.

A. Write and evaluate an expression that shows Lan’s age.
Answer:
Lan will be 9 years old in 3 years, so lan is
9 – 3 = 6 years old
B. Use Lan’s age to write and evaluate the expression for Liu Tse’s age.
Answer:
Liu Tse’s age is 30 years old.
6 + 4 × 6
6 + 24
30 years old.
Question 5.
Reason Ella has \(\frac{1}{3}\) as many trading cards as Kip. Adira has 3 more than 50% of the number of cards that Kip has. Kip has 18 cards.
A. Write an expression for the total number of cards the group has.
Answer:
\(\frac{1}{3}\) × 9 + (3 + 0.5 × 18) + 18
Explanation:
An expression for the total number of cards the group has \(\frac{1}{3}\) × 9 + (3 + 0.5 × 18) + 18
B. Evaluate the expression.
Answer:
33
Explanation:
The given expression is \(\frac{1}{3}\) × 9 + (3 + 0.5 × 18) + 18
Now we need to calculate the expression
\(\frac{1}{3}\) × 9 + (3 + 0.5 × 18) + 18
3 + (3 + 9) + 18
3 + (12) + 18
15 + 18
33
Question 6.
Use Tools Tamir bought 2\(\frac{1}{2}\) pounds of fish at $5.50 per pound, and two bananas at the price shown.

A. Write an expression to show how much change he received from a $20 bill.
_________________
Answer:
The expression to show how much change he received from a $20 bill is 20 – (2.5 × 5.5) – (2 × 0.45)
B. Evaluate the expression to show his change.
_________________
Answer:
8.8
Explanation:
The expression is 20 – (2.5 × 5.5) – (2 × 0.45)
20 – (12.1) – (0.9)
20 – 11.2
20 – 11.2
8.8
Question 7.
Tre is shown earning an hourly wage. An expression for the amount of money earned in one week is 16(3\(\frac{1}{2}\)) + 16(2\(\frac{1}{4}\)) + 16(5\(\frac{3}{4}\)) + 16(4\(\frac{1}{2}\)). Rewrite the expression so that it only has one multiplication operation, and then evaluate the expression.
Answer:

Question 8.
Attend to Precision Erin has 10 bags of apples. The following are the weights of the bags in pounds: 2\(\frac{1}{2}\), 2\(\frac{3}{4}\), 2\(\frac{1}{2}\), 2\(\frac{1}{4}\), 1\(\frac{1}{4}\), 2\(\frac{1}{2}\), 2\(\frac{1}{2}\), 1\(\frac{1}{4}\), 2\(\frac{1}{4}\), 2\(\frac{1}{4}\). Write an expression that shows the average weight of a bag. Evaluate the expression.
Answer:
Average weight of a bag is 2.2
Explanation:
Given,
2\(\frac{1}{2}\), 2\(\frac{3}{4}\), 2\(\frac{1}{2}\), 2\(\frac{1}{4}\), 1\(\frac{1}{4}\), 2\(\frac{1}{2}\), 2\(\frac{1}{2}\), 1\(\frac{1}{4}\), 2\(\frac{1}{4}\), 2\(\frac{1}{4}\)
Convert mixed fractions into improper fractions
\(\frac{5}{2}\), \(\frac{11}{4}\), \(\frac{5}{2}\), \(\frac{9}{4}\), \(\frac{5}{4}\), \(\frac{5}{2}\), \(\frac{5}{2}\), \(\frac{5}{4}\), \(\frac{9}{4}\), \(\frac{9}{4}\)
Now add all the number to find the average
\(\frac{5}{2}\) + \(\frac{11}{4}\) + \(\frac{5}{2}\) + \(\frac{9}{4}\) + \(\frac{5}{4}\) + \(\frac{5}{2}\) + \(\frac{5}{2}\) + \(\frac{5}{4}\) + \(\frac{9}{4}\) + \(\frac{9}{4}\)
(\(\frac{5}{2}\) + \(\frac{5}{2}\) + \(\frac{5}{2}\) + \(\frac{5}{2}\)) + (\(\frac{11}{4}\) + \(\frac{9}{4}\) + \(\frac{5}{4}\) + \(\frac{5}{4}\) + \(\frac{9}{4}\) + \(\frac{9}{4}\))
(\(\frac{20}{2}\) + \(\frac{48}{4}\))
10 + 12
22
The average weight of a bag id 22 ÷ 10 = 2.2
Question 9.
Rewrite the expression 6 ∙ (-\(\frac{3}{4}\)) + 2(\(\frac{1}{2}\)) – 2(\(\frac{3}{4}\)) using the Distributive Property. Then evaluate the expression.
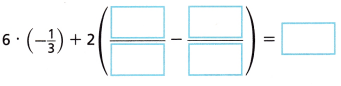
Answer:
Question 10.
Evaluate the expression [0.75 • (-12)] – (-6 ÷ \(\frac{2}{3}\)).
Answer:
0
Explanation:
Given,
[0.75 • (-12)] – (-6 ÷ \(\frac{2}{3}\))
[0.75 × (-12)] – (-6 × \(\frac{3}{2}\)
[-9] – (-3 × 3)
[-9] – (-9)
-9 + 9
0
Question 11.
Rewrite the expression –\(\frac{1}{4}\) • 3\(\frac{1}{3}\) • 8 (-1\(\frac{1}{5}\)) using the Commutative Property of Multiplication. Then evaluate the expression.
Answer:
8
Explanation:
Given,
–\(\frac{1}{4}\) × 3\(\frac{1}{3}\) × 8 (-1\(\frac{1}{5}\))
Convert the mixed fraction into improper fraction
–\(\frac{1}{4}\) × \(\frac{10}{3}\) × 8 (-\(\frac{6}{5}\))
\(\frac{1}{4}\) × \(\frac{10}{3}\) × 8 × \(\frac{6}{5}\)
Simply
2 × 2 × 2
8.
Question 12.
Rewrite the expression \(\frac{1}{2}\) • 33 • \(\frac{1}{11}\) using the Associative Property of Multiplication. Evaluate the expression.
Answer:
\(\frac{3}{2}\)
Explanation:
Given,
\(\frac{1}{2}\) × 33 × \(\frac{1}{11}\)
Cancel common factors
\(\frac{1}{2}\) × 3
\(\frac{3}{2}\)
Lesson 6.1 More Practice/Homework
Question 1.
Model with Mathematics Mr. Chung teaches a 1-hour math class. Six minutes are used for attendance and turning in homework. Then he teaches for 18 minutes. For the rest of the class, the students work on problems. For each problem, the students spend 3 minutes working on it, then Mr. Chung takes 6 minutes to explain it. After the class completes 4 problems, all of the class time is used up. Write and evaluate an expression to show this.
Answer:
33 minutes.
Explanation:
Attendance and turning in homework = 6 minutes
He teaches = 18 minutes
The students spend 3 minutes working on it
Mr. Chung takes 6 minutes to explain it.
The expression to show this is 6 + 18 + 3 + 6 = 33 minutes
Question 2.
Use Tools An online pet store ships 2 cases of dog food and 4 bags of treats. The dog food weighs 13\(\frac{1}{2}\) ounces per can, and there are 12 cans in a case. The dog treats are shown. Write and evaluate an expression to show the total weight of the items.

Answer:
The total weight of the items is 162.
Explanation:
The dog food weighs 13\(\frac{1}{2}\) = 13.5
In case there are 12 cans
13.5 × 12 = 162
Question 3.
Evaluate 5 – 44 ∙ (-0.75) – 18 ÷ \(\frac{2}{3}\) ∙ 0.8 + (-\(\frac{4}{5}\)).
Answer:
\(\frac{78}{5}\)
Explanation:
Let us evaluate the given expression
5 – 44 ∙ (-0.75) – 18 ÷ \(\frac{2}{3}\) ∙ 0.8 + (-\(\frac{4}{5}\)
5 + 44 × 0.75 – 18 ÷ \(\frac{2}{3}\) × 0.8 + (-\(\frac{4}{5}\)
5 + 33 – 18 ÷ \(\frac{2}{3}\) × 0.8 – \(\frac{4}{5}\)
Next divide a fraction by multipilying its reciprocal
5 + 33 – 18 × \(\frac{3}{2}\) × 0.8 – \(\frac{4}{5}\)
5 + 33 – 18 × \(\frac{3}{2}\) × \(\frac{8}{10}\) – \(\frac{4}{5}\)
Now cancel the common factors
5 + 33 – 9 × 3 × \(\frac{4}{5}\) – \(\frac{4}{5}\)
5 + 33 – (9 × 3 × 4) ÷ 5 – \(\frac{4}{5}\)
5 + 33 – \(\frac{108}{5}\) – \(\frac{4}{5}\)
(5 + 33) + (-\(\frac{108}{5}\) – \(\frac{4}{5}\))
38 + (-\(\frac{112}{5}\))
38 – \(\frac{112}{5}\)
\(\frac{190}{5}\) – \(\frac{112}{5}\)
\(\frac{78}{5}\).
Question 4.
The sum of 7 and 2.6 is multiplied by 9. Then this product is divided by the result of 4 – 2.8. Add parentheses to the expression, 9 7 + 2.6 ÷ 4 – 2.8, to show the correct order for the calculations described.
Answer:
[9 × (7 + 2.6)] ÷ (4 – 2.8)
Explanation:
From the given question the answer is
[9 × (7 + 2.6)] ÷ (4 – 2.8).
Question 5.
Use Structure This expression can be evaluated quickly by doing the computation in only one of the parentheses. Which set of parentheses is it, and what is the value of the expression? Explain.
-3(\(\frac{6}{11}\) + \(\frac{7}{19}\)) ∙ (-\(\frac{3}{8}\) + \(\frac{7}{15}\)) ∙ (-\(\frac{3}{2}\) + 2\(\frac{1}{8}\) – \(\frac{5}{8}\))
Answer:
Question 6.
A teacher gave a test with 50 questions, each worth the same number of points. Donovan got 39 out of 50 questions right. Marci’s score was 10 percentage points higher than Donovan’s. What was Marci’s score? Explain.
Answer:
88%
Explanation:
No of questions = 50
Donovan got 39 out of 50 questions right.
\(\frac{39}{50}\) = \(\frac{78}{100}\)
\(\frac{78}{100}\) + \(\frac{10}{100}\)
\(\frac{88}{100}\)
88%
Hence Marci scored \(\frac{44}{50}\) is the reasonable answer.
Test Prep
Question 7.
Which expression has a value of 7?
A. 4 + 0.5 × 8 – 2
B. (4 + 0.5) × 8 – 2
C. 4 + 0.5 × (8 – 2)
D. (4 + 0.5) × (8 – 2)
Answer:
4 + 0.5 × (8 – 2)
Explanation:
Let us solve the given expression to find the value of 7
Given expression is
4 + 0.5 × (8 – 2)
4 + 0.5 × 6
Find the multiplication
4 + 3
Now add the numbers
7
Question 8.
Chandra bought twice as many plants as Marvin. Kira bought \(\frac{1}{3}\) as many plants as Chandra. Marvin bought 6 plants. Write an expression that shows the total number of plants purchased. Who bought the most plants?
Answer:
Chandra bought the most plants.
Explanation:
There are three people buying a different number of plants.
Chandra bought twice as many plants as Marvin. Marvin bought 6 plants.
That means Chandra bought 6 × 2 = 12 plants
Kira bought \(\frac{1}{3}\) as many plants as Chandra, which means she bought
\(\frac{1}{3}\) × 12 = 4 plants
The total number of plants purchased = 4 + 12 + 6 = 22 plants
Hence Chandra bought 6 so she bought more plants.
Question 9.
The art class lasts 90 minutes. The teacher explains the project for 25 minutes and allows 15 minutes for questions and discussion. He talks to each student about their project for 5 minutes and then all of the class time is used up. Write and evaluate the expression that shows how many students are in the class.
Answer:
The expression shows how many students are in the class (90 – 25 -15) ÷ 15
Spiral Review
Question 10.
Evaluate -3 – (-3 – 7).
Answer:
Explanation:
Let us solve the given expression
-3 – (-3 – 7)
-3 – (-10)
-3 + 10
7
Question 11.
Evaluate 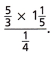
Answer:
2
Explanation:
(\(\frac{5}{3}\) × 1\(\frac{1}{5}\)) ÷ (\(\frac{1}{4}\))
(\(\frac{5}{3}\) × \(\frac{6}{5}\)) ÷ (\(\frac{1}{4}\))
\(\frac{3}{6}\) ÷ (\(\frac{1}{4}\)
\(\frac{3}{6}\) × 4
\(\frac{1}{2}\) × 4
2.
Question 12.
An account that yields 6% simple interest annually has $2,000. How much will be in the account after 3 years if no other deposits or withdrawals are made?
Answer:
2360
Explanation:
We know that R = 6%, P = 2000 and T = 3
Now calculate F = 2000 + 2000rt
F = 2000 (1 + rt)
Calculate the product = 2000 (1 + 0.18)
Calculate the sum = 2000 × 1.18
find the product = 2360
Question 13.
At the beginning of the month, Sammi has saved $120 in her bank account. She wants to buy a new gaming system for $200 in three weeks. She earns $20 a week. Will she have enough money at the end of three weeks to make the purchase? If not, how much more will she have to earn?
Answer:
No.
$120 + $60 is less than $200.
Therefore she needs $20 more.
Explanation:
We have to multiply how much she earns each week by the number of weeks and add it to her bank account. Then, subtract the amount in the bank after three weeks from the price of the gaming system to see how much more she needs.
$120 + $60 = $180
$200 – $180 = $20
She needs $20 more.