Into Math Grade 7 Module 5 Lesson 4 Answer Key Multiply and Divide Rational Numbers in Context

We included HMH Into Math Grade 7 Answer Key PDF Module 5 Lesson 4 Multiply and Divide Rational Numbers in Context to make students experts in learning maths.

HMH Into Math Grade 7 Module 5 Lesson 4 Answer Key Multiply and Divide Rational Numbers in Context

I Can multiply and divide rational numbers in context.

Step It Out

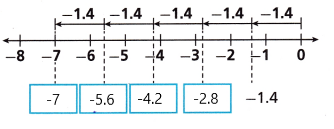
A hot air balloon is flying at an altitude of 570 meters. Air is released from the balloon in order to change the altitude by – 2.5 meters every second for 4 seconds. What is the new altitude of the balloon?

A. Write and use a model to find the change in altitude.

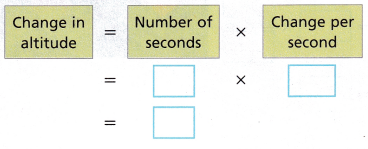
The altitude changes by ___ meters.
Answer:
The altitude changes by -10 meters.

The altitude of -10 means the altitude decreases by 10 meters.
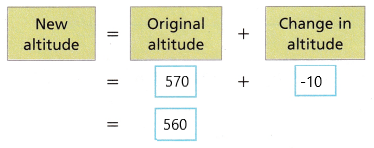
B. Write and use a model to find the new altitude.

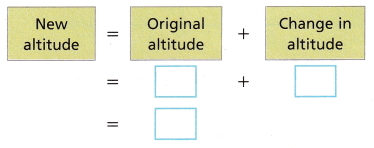
The new altitude is ____ meters.
Answer:
The new altitude is 560 meters.

C. Use a number line to show that your answer is reasonable.

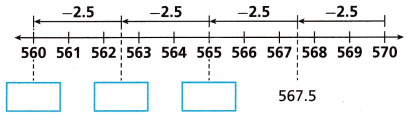
Answer:

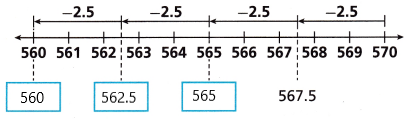
Turn and Talk Write and solve your own multiplication problem based on this situation.

2. In 4\(\frac{1}{2}\) minutes, a scuba diver swims from the surface to an elevation of -85 feet, swimming at a constant speed. Later, the diver swims upward 5 feet following a fish. Finally, the
diver takes 10\(\frac{2}{3}\) minutes to ascend to the surface, swimming at a constant speed.
A. Write and use a model to find how many feet the elevation changes every minute during the descent.


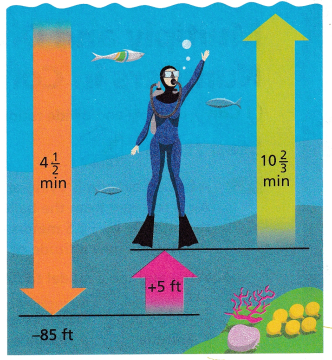
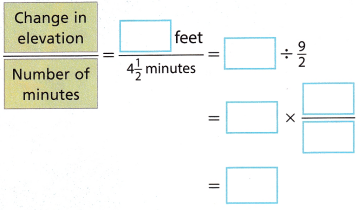
The elevation changes by about ___ feet every minute.
Answer:

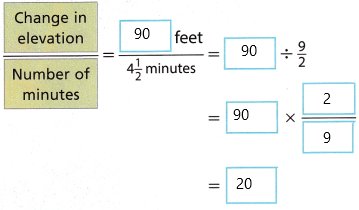
The elevation changes by about 20 feet every minute.

B. How do you know that your answer is reasonable?
_____________________
_____________________

Turn and Talk What is the scuba diver’s change in elevation in feet per minute during the final ascent? Explain.

Check Understanding

Question 1.
If the scuba diver in Task 2 originally swam -12\(\frac{1}{2}\) feet per minute, for 4\(\frac{1}{2}\) minutes, how would this change the situation?
Answer:
The change in situation is -56.25 feet.

Explanation:
Distance travelled per minute = -12\(\frac{1}{2}\) feet
Time travelled = 4\(\frac{1}{2}\) minutes
Change in elevation = Distance traveled per minute × Time traveled
= -12\(\frac{1}{2}\) × 4\(\frac{1}{2}\)
Convert them into improper fractions
= –\(\frac{25}{2}\) × \(\frac{9}{2}\)
= –\(\frac{225}{4}\)
= -56.25 feet.

Question 2.
Susan has \(\frac{3}{4}\) cup of raisins and she is dividing it into \(\frac{3}{8}\) cup servings. Complete the following. What does the answer represent?

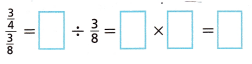
Answer:
The answer is 2.

Explanation:

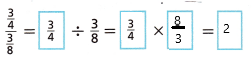
On Your Own

Question 3.
STEM Air temperature changes as you move away from Earth’s surface. Under certain conditions in Earth’s lower atmosphere, the temperature changes with increase in elevation as shown. Use this relationship to solve each problem.

A. Find and interpret the change in temperature for an increase in elevation of 0.2 mile.
_____________________
_____________________
Answer:
-3.76

Explanation:
Temperature change is about -18.8 F per mile
an increase in elevation of 0.2 mile
-18.8 × 0.2 = -3.76

B. Find and interpret the change in temperature for a decrease in elevation of 0.2 miles.
_____________________
_____________________
Answer:
3.76

Explanation:
Temperature change is about -18.8 F per mile.
Decrease in elevation of 0.2 miles
-18.8 × – 0.2 = 3.76

C. How are your answers to Parts A and B related?
_____________________
_____________________
Answer:
In part A when the elevation increases by 0.2 miles the temperature drops about 3.76° F.
In part B when the elevation decreases by 0.2 miles, the temperature rises about 3.76° F.

Question 4.
A butterfly is flying 8\(\frac{3}{4}\) feet above the ground. It descends at a steady rate to a spot 6\(\frac{1}{4}\) feet above the ground in 1\(\frac{2}{3}\) minutes. What is the butterfly’s change in elevation in feet per minute?
Answer:
The required change in elevation of the butterfly is 1.5 ft per min.

Explanation:
Given,
A butterfly is flying 8\(\frac{3}{4}\) feet above the ground.
It descends at a steady rate to a spot 6\(\frac{1}{4}\) feet above the ground in 1\(\frac{2}{3}\) minutes.
We have to find the butterfly’s change in elevation in feet per minute
Change in elevation = butterfly flying above ground – steady rate to a spot above the ground is
8\(\frac{3}{4}\) – 6\(\frac{1}{4}\)
\(\frac{35}{4}\) – \(\frac{25}{4}\)
\(\frac{10}{4}\)
\(\frac{5}{2}\)
2.5 feet
Now change in elevation per minute
= 1\(\frac{2}{3}\)
=  \(\frac{5}{3}\)
Change in elevation
2.5 ÷ \(\frac{5}{3}\)
2.5 × \(\frac{3}{5}\)
1.5 feet per minute.

Question 5.
One scuba diver’s elevation changed by -15\(\frac{5}{8}\) feet every minute. This was 1\(\frac{1}{4}\) times the rate of change for a second scuba diver. What was the rate
of change in elevation of the second scuba diver in feet per minute? Show your work.
Answer:
12.5 or 12\(\frac{1}{2}\)

Explanation:
Given,
scuba diver’s elevation changed by -15\(\frac{5}{8}\) feet every minute.
second scuba diver rate of change is 1\(\frac{1}{4}\)
15\(\frac{5}{8}\) ÷ 1\(\frac{1}{4}\)
\(\frac{125}{8}\) ÷ \(\frac{5}{4}\)
\(\frac{125}{8}\) × \(\frac{4}{5}\)
\(\frac{25}{2}\)
12.5 or 12\(\frac{1}{2}\).

Question 6.
Open Ended Write a real-world problem based on one of the contexts in the lesson that can be solved using multiplication or division of negative fractions or decimals.
Answer:
A store is selling a can of dog food for $0.40. Payal spent $4.80 on cans of dog food. Solve an equation to find how many cans shw bought $0.40.
No of cans = $4.80 ÷ $0.40
= 12 cans.

Question 7.
Carl has 3\(\frac{1}{2}\) cups of blueberries. He is storing them in containers that each hold \(\frac{2}{3}\) cup. How many containers can he fill? Find the answer and interpret the result.
Answer:
The total number of containers that can be filled = 5\(\frac{11}{50}\).

Explanation:
The blueberries carl has = 3\(\frac{1}{2}\) cups
= 3.5 cups
The amount of blueberries each container can store = \(\frac{2}{3}\)
= 0.67
Total cups = Total amount of blueberries to be stored ÷ Stored in one cup
= 3.5 cup ÷ 0.67
= 5.22
= 5\(\frac{11}{50}\).

Question 8.
Mrs. Anderson writes a check for $10.50 to each of her four nieces. What will be the total change in Mrs. Anderson’s checking account balance after all four checks are cashed? ____
Answer:
-42

Explanation:
Given,
Mrs. Anderson writes a check for $10.50 to each of her four nieces.
$10.50 × 4
42
They are asking how many checks were cashed, the answer will be negative.
= -42

Question 9.
The denominator of a fraction is \(\frac{-3}{4}\). The numerator is \(\frac{1}{4}\) more than the denominator. Identify the fraction. Then show that it is a rational number.
Answer:

Find each quotient.

Question 10.

Answer:
-3.5

Expression:
Let us solve the given expression
\(\frac{7}{10}\) ÷ – \(\frac{1}{5}\)
\(\frac{7}{10}\) × – 5
Cancel the common factors
–\(\frac{7}{2}\)
-3.5

Question 11.

Answer:
0.972

Explanation:
Let us solve the given expression
–\(\frac{5}{6}\) ÷ – \(\frac{6}{7}\)
–\(\frac{5}{6}\) × – \(\frac{7}{6}\)
\(\frac{35}{36}\)
0.972

Question 12.

Answer:
-168

Explanation:
Let us solve the given expression
\(\frac{252}{4}\) ÷ –\(\frac{3}{8}\)
252 ÷ 4 = 63
63 × –\(\frac{8}{3}\)
21 × -8
-168

Question 13.
\(\frac{2.8}{-4}\) _____________________
Answer:
–\(\frac{7}{10}\)

Explanation:
Let us solve the given expression
\(\frac{2.8}{-4}\)
–\(\frac{28}{(4 × 10)}\)
–\(\frac{7}{10}\)

Question 14.
–\(\frac{5.5}{0.5}\) _____________________
Answer:
-11

Explanation:
Let us solve the given expression
–\(\frac{5.5}{0.5}\)
Convert the decimal fractions into integers
–\(\frac{(55 × 10)}{(5 × 10}\)
Cancel all the common factors
-11

Question 15.
\(\frac{0.72}{-0.9}\) _____________________
Answer:
-0.8

Explanation:
Let us solve the given expression
\(\frac{0.72}{-0.9}\)
Convert the decimal fractions into integers
\(\frac{(72 × 10)}{(-9 × 100)}\)
–\(\frac{8}{10}\)
–\(\frac{4}{5}\)
-0.8

I’m in a Learning Mindset!

What questions can I ask my teacher to help me understand how to set up a problem that involves division?

Lesson 5.4 More Practice/Homework

Question 1.
Math on the Spot Sarah drove her police car at a constant speed down a mountain. Her elevation decreased by 200 feet over a 10-minute period. What was the change in elevation during the first minute?
Answer:
The change in elevation during the first minute is -20 feet.

Explanation:
Elevation decreased by 200 feet over a 10-minute period
200 ÷ 10
20
In her first minute, her elevation decreased by 20 feet.

Question 2.
A submarine descends \(\frac{1}{120}\) mile every minute. Write a product of three or more rational numbers to represent the change in the submarine’s elevation after 3 hours. Then find the value of the product, and explain what it represents.
Answer:
1.5 mile

Explanation:
Submarine descends \(\frac{1}{120}\) mile
submarine’s elevation after 3 hours
3 × 60 minutes
3 × 60 × \(\frac{1}{120}\)
3 × \(\frac{1}{2}\)
\(\frac{3}{2}\)
1.5 mile.

Question 3.
Financial Literacy Tanisha takes a dance class that is priced as shown. The charge appears as negative on her account balance until she makes her monthly payment.

A. Show how to find the balance of Tanisha’s account for dance classes during a 4-week period in which she attends 3 classes per week.
Answer:

Answer:
$37.5

Explanation:
Amount per class is $12.50
Now we need to find out Tanisha’s account for 3 classes per week.
one class per week = $12.50
3 classes per week = $12.50 × 3
= $37.5

B. Reason Suppose the balance on Tanisha’s account for a 2-week period is -$100. If Tanisha attended at least 1 dance class per week, how many classes could she have attended each week? Explain your reasoning.
Answer:
Tanisha attended 2 dance classes.
Given,
the balance on Tanisha’s account for a 2-week period is -$100
For 1 week it is – 100 ÷ 2
= -$50
Tanisha attended at least 1 dance class per week,
1 week = 1 dance class
Therefore Tanisha attended 2 dance classes for the balance on Tanisha’s account for a 2-week period is -$100.

C. Evaluate the expression -112.50 ÷ (-12.50) and interpret what it could mean in this context.
Answer:
9

Explanation:
Given,
the expression -112.50 ÷ (-12.50)
We need to evaluate the expression
Now cancel the minus symbol from both sides
112.50 ÷ 12.50
9

Find each quotient.

Question 4.

Answer:
–\(\frac{2}{3}\)

Explanation:
Let us solve the given expression
\(\frac{-5}{8}\) ÷ \(\frac{15}{16}\)
\(\frac{-5}{8}\) × \(\frac{16}{15}\)
Cancel the common factors
–\(\frac{2}{3}\)

Question 5.

Answer:
1.5

Explanation:
Let us solve the given expression
\(\frac{-2}{3}\) ÷ –\(\frac{4}{9}\)
Cancel the minus symbol from both sides
\(\frac{2}{3}\) × \(\frac{9}{4}\)
\(\frac{3}{2}\)
1.5

Question 6.

Answer:
-20

Explanation:
Let us solve the given expression
\(\frac{24}{7}\) ÷ \(\frac{-6}{35}\)
\(\frac{24}{7}\) × –\(\frac{35}{6}\)
Cancel the common factors
4 × -5
-20

Test Prep

Question 7.
Salton Sea Beach in California has an elevation of about – 230 feet. This is about 11.5 times the elevation of Indio, California. What is the elevation of Indio, California?
about ___ feet
Answer:
-20

Explanation:
California has an elevation of about – 230 feet.
11.5 times the elevation of Indio, California
-230 ÷ 11.5
= -20

Question 8.
During a winter cold spell, the temperature change was – 1.2 °F per hour for a period of 4.5 hours. Which expressions can be used to find the overall change in temperature during that time period?
A. 4.5 ÷ (-1.2) degrees Fahrenheit
B. 4.5 × (- 1.2) degrees Fahrenheit
C. 4.5 – (- 1.2) degrees Fahrenheit
D. (-1.2) + (-1.2) + (-1.2) + (-1.2) degrees Fahrenheit
E. 4(- 1.2) + (0.5)(-1.2) degrees Fahrenheit
Answer:
B. 4.5 × (- 1.2) degrees Fahrenheit

Explanation:
The expressions can be used to find the overall change in temperature during that time period is 4.5 × (- 1.2) degrees Fahrenheit.

Question 9.
Which expression is equivalent to ?
A. –\(\frac{5}{6}\) ÷ \(\frac{3}{10}\)
B. –\(\frac{5}{6}\) ÷ \(\frac{10}{3}\)
C. –\(\frac{5}{6}\) × \(\frac{10}{3}\)
D. –\(\frac{6}{5}\) × \(\frac{3}{10}\)
Answer:
B. –\(\frac{5}{6}\) ÷ \(\frac{10}{3}\)

Explanation:
The expression is equivalent to is –\(\frac{5}{6}\) ÷ \(\frac{10}{3}\).

Spiral Review

Question 10.
What is the difference when – 2 is subtracted from 2?
Answer:
4

Explanation:
The difference when – 2 is subtracted from 2 is 4.
2 – (-2) = 4

Question 11.
Complete the number line diagram. What addition problem does the diagram represent?

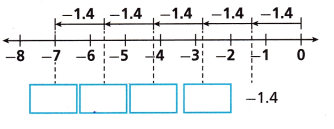
Answer: