We included HMH Into Math Grade 7 Answer Key PDF Module 5 Lesson 3 Write Fractions as Decimals and Divide Integers to make students experts in learning maths.
HMH Into Math Grade 7 Module 5 Lesson 3 Answer Key Write Fractions as Decimals and Divide Integers
I Can express quotients in different forms.
Spark Your Learning
Hayley is buying herbs. She wants to buy \(\frac{5}{6}\) ounce of basil. The scale she is using to weigh the basil displays the weight as a decimal. How will she know when the display on the scale is correct to the tenths place? Explain your reasoning.


Answer:

Turn and Talk What do you think the digit in the hundredths place of the display will be? Explain your reasoning.
The next digit after the decimal represents hundredths place.
Build Understanding
1. Hayley wants to buy the amounts of herbs shown. How can you convert these fractions to decimals?
A. You can use equivalent fractions to convert a fraction to a decimal. Does that method work well for these fractions? Why or why not?

Answer:
Given,
\(\frac{3}{4}\) = 0.75
\(\frac{2}{3}\) = 0.66
B. You can also use long division to convert a fraction to a decimal, because \(\frac{a}{b}\) = a ÷ b for all fractions \(\frac{a}{b}\).
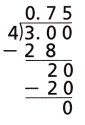
_______________________
_______________________
C. How can you use the decimal form of \(\frac{3}{4}\) ounce to find what Hayley will pay for basil that costs $5.80 per ounce?
Answer:
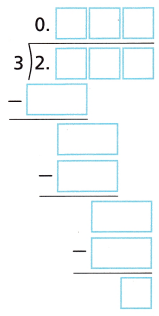
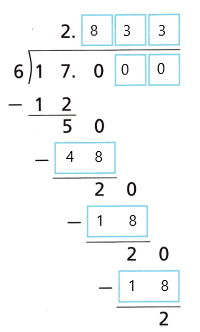
D. Use long division to find the decimal equivalent of ounce to the thousandths place. Do not round.
_______________________
Answer:
1 ounce = \(\frac{1}{16}\)
0.0625
E. Describe the pattern in the quotient. Will the ‘pattern continue if you write a zero in the ten-thousandths place of the dividend and continue dividing? Why or why not?
_______________________
_______________________
_______________________
Turn and Talk Can the number 20 be divided evenly by 3? What does your answer imply about the quotient in Step E? Explain.
Answer:
The number 20 cannot be divided evenly.
20 ÷ 3
6.66 is a repeating decimal.
Step It Out
2. Every quotient of integers is a rational number provided that the divisor is not zero. Every rational number can be written as a fraction in which the numerator and the denominator are integers. The fraction can be written as a decimal that either terminates (ends) or repeats.
Examples: terminating decimal: \(\frac{3}{4}\) = 0.75
repeating decimal: \(\frac{2}{3}\) = 0.666…, or \(0 . \overline{6}\)
Answer:
The bar over the 6 means that it repeats forever.
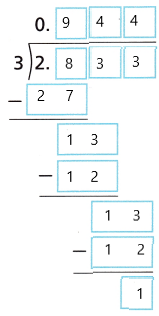
A. Suppose Hayley wants to buy 2\(\frac{5}{6}\) ounces of basil. Complete the statement to show that 2\(\frac{5}{6}\) a rational number.
2\(\frac{5}{6}\) = ![]() and ___ and ___ are integers.
and ___ and ___ are integers.
Answer:
2\(\frac{5}{6}\)
\(\frac{17}{6}\)
2.8333
So 2\(\frac{5}{6}\) is a rational number.
17 and 6 are integers.
B. Complete the long division shown to write 2\(\frac{5}{6}\) as a decimal. Then complete the statement.
2\(\frac{5}{6}\) = ___, which is a (terminating / repeating) decimal.
Answer:

2.833 is a repeating decimal.
3. Use the rules you’ve learned for dividing negative numbers.
A. Find each quotient. Then complete the statement.
\(\frac{15}{-3}\) = ____ ÷ ____ = _____
\(\frac{-15}{3}\) = ____ ÷ ____ = _____
–\(\left(\frac{15}{3}\right)\) = ____
The rational numbers \(\frac{15}{-3}\), \(\frac{-15}{3}\) and \(\left(\frac{15}{3}\right)\) (are/are not) equivalent.
Answer:
\(\frac{15}{-3}\) = 15 ÷ -3 = -5
\(\frac{-15}{3}\) = -15 ÷ 3 = -5
–\(\left(\frac{15}{3}\right)\) = -5
The rational numbers \(\frac{15}{-3}\), \(\frac{-15}{3}\) and \(\left(\frac{15}{3}\right)\) are equivalent.
B. If p and q are integers and q is not zero, what can you conclude about \(\frac{-p}{q}\), \(\frac{p}{-q}\) and –\(\left(\frac{p}{q}\right)\)?

Answer:
Given,
p and q are integers.
\(\frac{-p}{q}\), \(\frac{p}{-q}\) and –\(\left(\frac{p}{q}\right)\)
A number that is expressed in the form of \(\frac{p}{q}\), where p and q are integers and q is not zero is called a rational number.5
C. Suppose .that the value of a share of stock decreased by $15 in 3 days. Which expression in Part A best represents the average daily change in the stock’s value? Explain.
_______________________
_______________________
Answer:
The expression \(\frac{15}{-3}\) in Part A best represents the average daily change in the stock’s value.
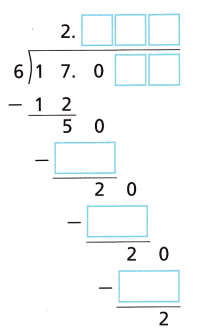
Turn and Talk Is the number -2\(\frac{5}{6}\) a rational number? Why or why not?
Answer:
Given,
-2\(\frac{5}{6}\) = –\(\frac{17}{6}\) is a rational number.
Explanation:
A rational number can be expressed as the ratio of two numbers where numerator and denominator will not be equal to each other. So the given number -2\(\frac{5}{6}\) = –\(\frac{17}{6}\) is a rational number.
On Your Own
Question 4.
Rafael is buying 1\(\frac{3}{8}\) pounds of salad at a salad bar that charges the amount shown.

A. Show that the amount of salad is a rational number.
_______________________
Answer:
1.375 is a rational number.
Explanation:
Given,
1\(\frac{3}{8}\) pounds
\(\frac{11}{8}\)
1.375
1.375 is a finite decimal, finite decimals are called rational numbers. So the amount of salad is a rational number.
B. Write the amount of salad as a decimal.
_______________________
Answer:
The amount of salad as a decimal is 1.375.
C. What will Rafael pay for the salad?
_______________________
Answer:
9.35
Explanation:
A salad bar is $6.80
Rafael bought 1\(\frac{3}{8}\) pounds of salad
\(\frac{11}{8}\)
\(\frac{11}{8}\) × 6.80
1.375 × 6.80
9.35
Question 5.
The temperature dropped steadily by 40 °F over a 20-hour period. Find the quotient —40 ÷ 20 and explain what it means in this context.
_______________________
Answer:
The quotient of -40 ÷ 20 = -20
Explanation:
The temperature dropped steadily by 40 °F
Time = 20 hour period
The quotient of -40 ÷ 20 = -20 °F
Question 6.
The balance on Mr. Finchs credit card is -$210. It is 3 times the balance on Mr. Nguyen’s credit card. Find the quotient -210 ÷ 3 and explain what it means in this context.
Answer:
The quotient is -70. The balance on Mr. Nguyen’s credit card is -70.
Explanation:
The balance on Mr. Finchs credit card is -$210.
The balance is three times the balance on Mr. Nguyen’s credit card.
The quotient -210 ÷ 3 = -70
The balance on Mr. Nguyen’s credit card is -70.
Question 7.
Use Repeated Reasoning Use the table shown.
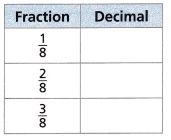
A. Convert each fraction in the table to a decimal. Describe a pattern in the results.
_______________________
Answer:
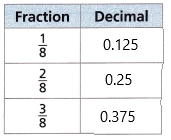
The pattern followed in the diagram is n, n+1, n+2, n+3, and so on.
\(\frac{1}{8}\), \(\frac{2}{8}\), \(\frac{3}{8}\), \(\frac{4}{8}\), \(\frac{5}{8}\),
B. Does this pattern continue? Why or why not?
_______________________
Answer:
Yes, the pattern continues. Because the numbers are consecutive natural numbers.
Question 8.
Michelle has to find the decimal equivalent of 15\(\frac{1}{8}\) yards. How can she do this without first writing the mixed number as a fraction?
_______________________
Answer:
15.125
Explanation:
Given,
the decimal equivalent of 15\(\frac{1}{8}\) yards
\(\frac{121}{8}\)
15.125
Question 9.
The value of a gift card to a rock climbing gym decreased by $34 after 4 equal charges to the card. Find the quotient -34 ÷ 4 and explain what it means in this context.

Answer:
The quotient -34 ÷ 4 = -8.5
Explanation:
The quotient -8.5 is a decimal number and also an integer.
Question 10.
Reason Are all integers rational numbers? Explain.
Answer:
Yes, all integers are rational numbers because integers are the set of numbers with all the positive counting numbers.
Convert each number to a decimal.
Question 11.
\(\frac{5}{8}\) _______________________
Answer:
0.625
Explanation:
Given,
\(\frac{5}{8}\)
0.625
The division for the given number \(\frac{5}{8}\) is 0.625.
Question 12.
\(\frac{5}{16}\) _______________________
Answer:
0.3125
Explanation:
The division for the given number is 0.3125.
Given,
\(\frac{5}{16}\)
0.3125
Question 13.
\(\frac{7}{9}\) _______________________
Answer:
0.777
Explanation:
The division for the given number is 0.777.
Given,
\(\frac{7}{9}\)
0.777
Question 14.
1\(\frac{1}{6}\) _______________________
Answer:
The division for the given number is 1.16
Explanation:
Given,
1\(\frac{1}{6}\)
\(\frac{7}{6}\)
1.16
Question 15.
10\(\frac{4}{11}\) _______________________
Answer:
10.36
Explanation:
Given,
10\(\frac{4}{11}\)
\(\frac{114}{11}\)
10.36
Question 16.
7\(\frac{3}{11}\) _______________________
Answer:
7.27
Explanation:
Given,
7\(\frac{3}{11}\)
\(\frac{80}{11}\)
7.27
Write two fractions equivalent to the given fraction.
Question 17.
\(\frac{-3}{5}\) _______________________
Answer:
-0.6
Explanation:
Given,
\(\frac{-3}{5}\)
–\(\frac{3}{5}\)
-0.6
Question 18.
\(-\left(\frac{7}{10}\right)\) _______________________
Answer:
-0.7
Explanation:
Given,
\(-\left(\frac{7}{10}\right)\)
-0.7
Question 19.
Explain why -7\(\frac{3}{5}\) is a rational number.
_______________________
Answer:
–\(\frac{38}{5}\) or -7.6
Explanation:
Given,
-7\(\frac{3}{5}\)
–\(\frac{38}{5}\)
– 7.6
Find each quotient.
Question 20.
-84 ÷ 7 ____
Answer:
-12
Explanation:
The division of the given numbers is -12.
Question 21.
-52 ÷ (-4) _____
Answer:
13
Explanation:
The division of the given numbers is 13.
(-) + (-) = (+)
Question 22.
\(\frac{-69}{-11}\)
Answer:
6.27
Explanation:
Given,
\(\frac{-69}{-11}\)
6.27
Question 23.
\(\frac{60}{-8}\)
Answer:
-7.5
Explanation:
Given,
\(\frac{60}{-8}\)
\(\frac{30}{-4}\)
–\(\frac{15}{2}\)
Question 24.
Open Ended Write two quotients of integers that can be converted to terminating decimals and two that can be converted to repeating decimals.
_______________________
Answer:
I’m in a Learning Mindset!
How effective was using long division to write a fraction as a decimal? Do I still have questions?
Answer:
Long division method is used to divide large numbers into multiple smaller groups. So these can be written as a decimal.
Lesson 5.3 More Practice/Homework
Question 1.
Sean is buying \(\frac{9}{6}\) pound of tea at a tea shop. The cost of the tea is shown.
A. Write the amount of tea as a decimal.
_______________________
Answer:
1.5
Explanation:
Given,
\(\frac{9}{6}\) = 1.5

B. What will Sean pay for the tea?
_______________________
Answer:
Sean will pay 36 for the Tea.
Explanation:
\(\frac{9}{6}\) × 24
9 × 4 = 36
Convert each number to a decimal.
Question 2.
\(\frac{1}{3}\)
Answer:
0.33
Explanation:
Given,
\(\frac{1}{3}\)
Convert them into decimal fraction
0.33
Question 3.
4\(\frac{7}{8}\)
Answer:
4.875
Explanation:
Given,
4\(\frac{7}{8}\)
\(\frac{39}{8}\)
4.875
Question 4.
Write three fractions equivalent to the quotient 50 ÷ (-17) using only the numbers -50, -17, 17, or 50. Then explain why a quotient is a rational number.
_______________________
Answer:
-2.94
Explanation:
Given,
quotient 50 ÷ (-17)
Remove the parentheses -50 ÷ 17
Rewrite as fraction \(\frac{-50}{17}\)
–\(\frac{50}{17}\)
-2.94
Find each quotient.
Question 5.
42 ÷ (-7) ____
Answer:
-6
Explanation:
The division of the given numbers is 42 ÷ (-7) = -6
Question 6.
-56 ÷ 8 ____
Answer:
-7
Explanation:
The division of the given numbers is -56 ÷ 8 = -7
Question 7.
\(\frac{-27}{5}\) _______________________
Answer:
-5.4
Explanation:
Given,
\(\frac{-27}{5}\)
-5.4
Question 8.
\(\frac{35}{-3}\) _______________________
Answer:
-11.66
Explanation:
Given,
\(\frac{35}{-3}\)
-11.66
Question 9.
Use Repeated Reasoning Use the table shown.
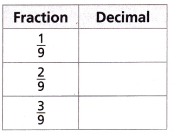
A. Convert each fraction in the table to a decimal. Describe a pattern in the results.
_______________________
Answer:
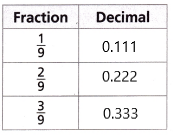
The pattern is n, n+1, n+2, n+3 and so on
Here n= 1
therefore 1, 2, 3 and so on
B. Does this pattern continue? Why or why not?
_______________________
Answer:
Test Prep
Question 10.
Which of the following are equivalent to \(-\left(\frac{a}{b}\right)\)? Select all that apply.
A. \(\frac{a}{b}\)
B. \(\frac{-a}{-b}\)
C. \(\frac{-a}{b}\)
D. \(\frac{a}{-b}\)
E. -(\(\frac{a}{-b}\))
Answer:
C. \(\frac{-a}{b}\)
D. \(\frac{a}{-b}\)
Explanation:
The given options C and D are equivalent to \(-\left(\frac{a}{b}\right)\).
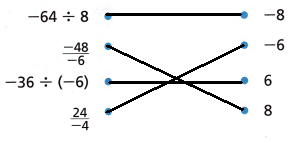
Question 11.
Draw a line to match each quotient to its value.

Answer:
Spiral Review
Question 12.
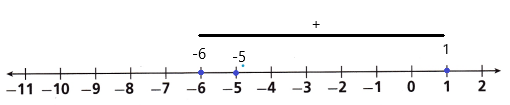
Use the number line to show how to find the given difference. Then write an equivalent addition expression.
1 – 6 = ___
Answer:
-5
Explanation:
Question 13.
In 2016, the price of a stock decreased by $11. In 2017, the price decreased by $13. Write a sum of two integers that represents the overall change in the price of the stock for the two years. Then find the sum and explain what it tells you about the price of the stock.
Answer:
The sum of two integers that represents the overall change in the price of the stock for the two years is -11 + (-13) = -24
Explanation:
Given,
the price of a stock decreased by $11
the price decreased by $13.
The sum of two integers that represents the overall change is -11 + (-13) = -24
This shows that the stock has decreased by 24.
Question 14.
Audra has a subscription to a news site. To pay for the subscription, $8 is automatically deducted from her checking account once per month.
A. Write a product of three or more integers that represents the change in Audra’s account after three years.
_______________________
Answer:
The change in Audra’s account after three years is 8760.
Explanation:
We need to find the Audra’s account after three years.
1 year = 365 days
$8 is automatically deducted from her checking account once per month.
365 + 365 + 365 =1095
1095 × 8 = 8760
B. What integer represents the change in Audra’s account after three years?
_______________________
Answer:
365
Explanation:
The integer that represents the change in Audra’s account after three years is 365.