Into Math Grade 7 Module 4 Lesson 4 Answer Key Apply Properties to Multi-step Addition and Subtraction Problems

We included HMH Into Math Grade 7 Answer Key PDF Module 4 Lesson 4 Apply Properties to Multi-step Addition and Subtraction Problems to make students experts in learning maths.

HMH Into Math Grade 7 Module 4 Lesson 4 Answer Key Apply Properties to Multi-step Addition and Subtraction Problems

I Can Identify and write expressions to represent multi-step addition and subtraction problems.

Step It Out

1. Andy usually skates for about 6 hours per week. On Monday, he spent 1\(\frac{1}{5}\) hours skating; on Wednesday, he spent 2\(\frac{3}{5}\) hours skating; and on Thursday, he spent 1\(\frac{5}{6}\) hours skating. Andy wrote the following expression to find the number of hours he spent skating. He grouped Wednesday and Thursday together at first because those were his best days, without thinking too much about what would be easiest to add.
1\(\frac{1}{5}\) + (2\(\frac{3}{5}\) + 1\(\frac{5}{6}\))

A. Rewrite the expression to make it simpler to add.
(____ + 2\(\frac{3}{5}\)) + ____
Answer:
(1\(\frac{1}{5}\) + 2\(\frac{3}{5}\)) + 1\(\frac{5}{6}\)
B. What property ¡s demonstrated by rewriting the expression?
_____________________
Answer:
The property used to rewrite the expression is the associative property of addition.
C. Regrouping makes the problem simpler because it associates two numbers with _____________________
Answer: Regrouping makes the problem simpler because it associates two numbers with brackets.

D. To add the numbers in parentheses,
Add the whole numbers: 1 + ___ = ___
Add the like fractions: \(\frac{1}{5}\) + ___ = ____
Combine the results: _____
Answer:
Add the whole numbers: 1 + 2 = 3
Add the like fractions: \(\frac{1}{5}\) + \(\frac{3}{5}\) = \(\frac{4}{5}\)
Combine the results: 3 + \(\frac{4}{5}\) = 3 \(\frac{4}{5}\)

E. Use your result from Part D to finish evaluating the expression.

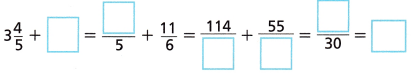
Answer:

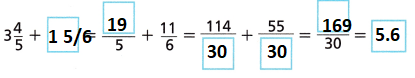
Turn and Talk Is there another way to solve this problem? Explain.

2. Rochelle dives into a lake from the water’s surface. Her change in elevation in the lake is described. She:

• descends 15.5 feet and takes some pictures of fish;
• ascends 8\(\frac{1}{5}\) feet to explore another area;
• descends 1.6 feet to capture video while following a fish;
• descends 20.4 feet to find some feeding bass; and finally,
• ascends 15.5 feet to take more pictures.

How many feet does Rochelle have left to ascend before reaching the surface?

A. Write an addition expression to represent Rochelle’s change in elevation from the water’s surface.
_________________________
Answer: 8\(\frac{1}{5}\) + 15.5
B. Rewrite the expression to make it simpler to find the sum by first adding opposites.
_________________________
Answer: 8\(\frac{1}{5}\) + 15.5
C. What properties of operations did you use to rewrite your expression in Part B?
_________________________
_________________________
D. Add the opposites in your expression in Part B, and write the resulting expression.
_________________________

E. Evaluate your expression in Part D to determine Rochelle’s elevation relative to the water’s surface.
Identify the property used in the second line.
8\(\frac{1}{5}\) + ____ + ____
= 8\(\frac{1}{5}\) + ____ ______
= 8.2 + ____
= _____
Rochelle is ___ feet below the water’s surface.
Answer:
8\(\frac{1}{5}\) + 15.5 + 37.5
= 8\(\frac{1}{5}\) + 15.5 + 37.5
= 8.2 + 15.5 + 37.5
= 61.2
Rochelle is 61.2 feet below the water’s surface.

Turn and Talk How are the properties of addition used to evaluate the expression in Task 2?

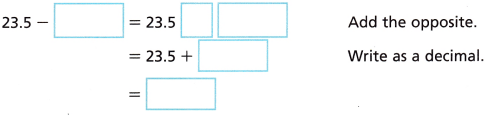
3. Terry is hiking in a valley at its lowest elevation. Abe is hiking on a different trail at an elevation of 23.5 meters above sea level. How much higher in elevation is Abe than Terry?

A. How should elevation below sea level be written?
__________________
Answer: Elevations below sea level are written in negative.
B. Since one number is a decimal and one contains a fraction, you must either convert the decimal to a
____ or the fraction to a ____ before evaluating.
Answer:
Convert the fraction into a decimal form before evaluating.
C. Complete the expression to show the difference between their elevations. Then evaluate the expression to solve the problem.

Abe is ___ meters higher in elevation than Terry.
Answer:
23.5 – 19 \(\frac{3}{4}\)
23.5 – 19.75
23.5 + 19.75 = 43.25

D. Is your answer reasonable? Explain.
_________________________
_________________________
_________________________
_________________________

Turn and Talk If Abe’s elevation was —23.5 meters iñstead of +23.5 meters, what would Terry and Abe’s elevation difference be then? Explain.
Answer: -23.5 + 19.75 = -3.75

Check Understanding

Question 1.
Soojin is adding some lengths of wood she used for a project. The lengths of wood are 1\(\frac{2}{3}\), 3\(\frac{3}{4}\), and 2\(\frac{1}{4}\) feet. How much wood did she use in all?
Answer:
Given,
Soojin is adding some lengths of wood she used for a project.
The lengths of wood are 1\(\frac{2}{3}\), 3\(\frac{3}{4}\), and 2\(\frac{1}{4}\) feet.
2\(\frac{1}{4}\) + (1\(\frac{2}{3}\) + 3\(\frac{3}{4}\))
2\(\frac{1}{4}\) + (1 + \(\frac{2}{3}\) + 3 + \(\frac{3}{4}\))
2\(\frac{1}{4}\) + ( 4 + \(\frac{2}{3}\) + \(\frac{3}{4}\))
2\(\frac{1}{4}\) + ( 4 + \(\frac{8}{12}\) + \(\frac{9}{12}\))
2\(\frac{1}{4}\) + ( 4 + \(\frac{17}{12}\))
2\(\frac{1}{4}\) + ( 4 + 1 \(\frac{5}{12}\))
2\(\frac{1}{4}\) + 5 \(\frac{5}{12}\)
2 + \(\frac{1}{4}\) + 5 + \(\frac{5}{12}\)
2 + 5 = 7
\(\frac{1}{4}\) + \(\frac{5}{12}\)
\(\frac{3}{12}\) + \(\frac{5}{12}\) = \(\frac{8}{12}\) = \(\frac{2}{3}\)
7 + \(\frac{2}{3}\) = 7\(\frac{2}{3}\)

Question 2.
Alfonzo started with $50.00 in his checking account. He recorded these transactions in his checkbook: -$12.75, -$5.43, $75.00, -$2.57, and -$22.25. How can you use the Commutative and Associative Properties of Addition to find his balance using mental math?
Answer:
Given,
Alfonzo started with $50.00 in his checking account. He recorded these transactions in his checkbook: -$12.75, -$5.43, $75.00, -$2.57, and -$22.25
50 – 12.75 – 5.43 + 75 – 2.57 – 22.25
50 + 75 – (12.75 + 22.25 + 5.43 +2.57) (commutative law)
50 + 75 – (12.75 +22.25) – (5.43 + 2.57) (associative law)
50 + 75 – 25 – 8
50 + 50 – 8 = 92

On Your Own

Question 3.
Use Structure Dena cuts wood for a treehouse. She has five pieces of wood left over with the following lengths in centimeters: 12.7, 26\(\frac{3}{10}\), 15\(\frac{4}{5}\), 21\(\frac{1}{4}\), and 19.2.
A. Write and evaluate an expression to find the total length of wood left over.
_____________________
Answer:
Total length = 12.7 + 26\(\frac{3}{10}\) + 15\(\frac{4}{5}\) + 21\(\frac{1}{4}\) + 19.2

B. Dena wants to make a birdhouse with the leftover wood. She needs 105\(\frac{3}{5}\) centimeters of wood for the birdhouse. Write and evaluate an expression to determine how much more wood will be needed.
Answer:
Total length = 12.7 + 26\(\frac{3}{10}\) + 15\(\frac{4}{5}\) + 21\(\frac{1}{4}\) + 19.2
= 12\(\frac{7}{10}\) + 26\(\frac{3}{10}\) + 15\(\frac{4}{5}\) + 21\(\frac{1}{4}\) + 19 \(\frac{4}{20}\)
= (12\(\frac{7}{10}\) + 26\(\frac{3}{10}\)) + 15\(\frac{4}{5}\) + 21\(\frac{1}{4}\) + 19 \(\frac{4}{20}\)
= 39 + 56\(\frac{5}{20}\)
= 95 \(\frac{1}{4}\)

Question 4.
Use Repeated Reasoning The table shows the highest and lowest elevations in four states.

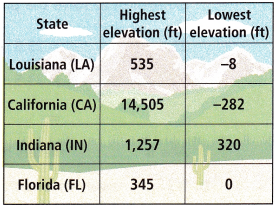
A. Write and evaluate an expression to find the difference in elevation in each state.
____________________________
____________________________
____________________________
____________________________
Answer:
Louisiana = 535 – (-8) = 535 + 8 = 543
California = 14,505 – (-282) = 14505 + 282 = 14787
Indiana = 1257 – 320 = 937
Florida = 345 – 0 = 345

B. Roger says the difference between the lowest elevation in California and the lowest elevation in Louisiana is -290 feet. Determine if his answer is reasonable. Explain.
___________________
Answer:
-282 – (-8)
-282 + 8 = -274 feet

Question 5.
The high temperatures (in °F) for a 4-day holiday weekend were:
-2.6, 16.7, -3.4, 6.1
Use properties of addition to help you find the sum. Then find the average high temperature over the four days.
_________________________
_________________________
Answer:
The high temperatures (in °F) for a 4-day holiday weekend were:
-2.6, 16.7, -3.4, 6.1
-2.6 + 16.7 – 3.4 + 6.1 = 16.8
Average of 4 days:
16.8/4 = 4.2°F

For Problems 6—11. evaluate each expression.

Question 6.
2.6 + (-3.7 – (-1.5))
Answer:
2.6 + (-3.7 – (-1.5))
2.6 – 3.7 + 1.5
2.6 + 1.5 – 3.7 = 0.4

Question 7.
-15 – 2\(\frac{3}{4}\) – 1.7 – (-2\(\frac{2}{5}\))
____________________________
Answer:
-15 – 2\(\frac{3}{4}\) – 1.7 – (-2\(\frac{2}{5}\))
-15 – 2.75 – 1.7 – (-2.4)
-15 – 2.75 – 1.7 + 2.4 = -17.05
Thus -15 – 2\(\frac{3}{4}\) – 1.7 – (-2\(\frac{2}{5}\)) = -17.05

Question 8.
-1\(\frac{1}{5}\) + 2.9 – (-3\(\frac{3}{8}\))
Answer:
-1\(\frac{1}{5}\) + 2.9 – (-3\(\frac{3}{8}\))
-1.2 + 2.9 + 3\(\frac{3}{8}\)
-1.2 + 2.9 + 3.375 = 5.075
Thus, -1\(\frac{1}{5}\) + 2.9 – (-3\(\frac{3}{8}\)) = 5.075

Question 9.
2\(\frac{3}{4}\) + (-8.34) + (-7\(\frac{3}{10}\))
Answer:
2\(\frac{3}{4}\) + (-8.34) + (-7\(\frac{3}{10}\))
2.75 – 8.34 – 7.3 = -12.89
Thus, 2\(\frac{3}{4}\) + (-8.34) + (-7\(\frac{3}{10}\)) = -12.89

Question 10.
-11.5 + 15\(\frac{2}{5}\) – 10.1
Answer:
-11.5 + 15\(\frac{2}{5}\) – 10.1
-11.5 + 15.4 – 10.1 = -6.2
-11.5 + 15\(\frac{2}{5}\) – 10.1 = -6.2

Question 11.
5\(\frac{1}{4}\) – (-3.55) + (-3\(\frac{2}{5}\))
Answer:
5\(\frac{1}{4}\) – (-3.55) + (-3\(\frac{2}{5}\))
5.25 + 3.55 – 3.40 = 5.40

Question 12.
Use Repeated Reasoning Ella dives three times into a lake. Her elevations relative to the water’s surface are -6.9 feet, -8\(\frac{2}{5}\) feet, and -7.5 feet. She dives three more times with each dive 0.75 feet deeper than each of the first three. Write and evaluate expressions to determine the elevations, in decimal form, of her fourth, fifth, and sixth dives.

Answer:
Given,
Ella dives three times into a lake. Her elevations relative to the water’s surface are -6.9 feet, -8\(\frac{2}{5}\) feet, and -7.5 feet.
She dives three more times with each dive 0.75 feet deeper than each of the first three.
-6.9 – 0.75 = -7.65
-8\(\frac{2}{5}\) = -8.4 – 0.75 = -9.15
-7.5 – 0.75 = -8.25

Question 13.
Financial Literacy Chris wrote the following checks: $19.50, $25.75, $5.50, and $136.95. He began with $252.17 in his checking account. Write and evaluate an expression to determine his balance.
Answer:
Given,
Chris wrote the following checks: $19.50, $25.75, $5.50, and $136.95.
He began with $252.17 in his checking account.
252.17 – 136.95 – 5.5 – 19.5 – 25.75
115.22 – 5.5 – 19.5 – 25.75
109.72 – 19.5 – 25.75
90.22 – 25.75
64.47

Question 14.
Reason Beylinn is driving on a road with an elevation of -245\(\frac{5}{8}\) meters. Jay is driving on a different road at an elevation of -56.45 meters. Write and evaluate an expression to determine who is traveling at a higher elevation. How much higher? Explain.
_________________________
_________________________
Answer:
Given,
Berlin is driving on a road with an elevation of -245\(\frac{5}{8}\) meters. Jay is driving on a different road at an elevation of -56.45 meters.
-245\(\frac{5}{8}\) – (-56.45)
245\(\frac{5}{8}\) can be written in the decimal as 245.625
-245.625 + 56.45 = -189.175
Height cannot be negative so, it is 189.75 meters taller.

Question 15.
Dino is learning to scuba dive. First, he descended 27.75 feet. After ten minutes, he descended another 9.45 feet. Write and evaluate an expression to determine his elevation relative to sea level.
Answer:
Given,
Dino is learning to scuba dive. First, he descended 27.75 feet. After ten minutes, he descended another 9.45 feet.
27.75 + 9.45 = 37.2 feet
Dino elevation relative to sea level is 37.2 feet.

Question 16.
Explain why you might want to use properties to change the order and grouping of the numbers in the following sum.
-45.2 + (-7.9) + (-3.8)
Answer:
-45.2 + (-7.9) + (-3.8)
-45.2 – 7.9 – 3.8 = -56.9

For Problems 17—24, evaluate each expression.

Question 17.
-12\(\frac{2}{5}\) + 8\(\frac{9}{10}\)
__________________
Answer:
-12\(\frac{2}{5}\) + 8\(\frac{9}{10}\)
-12 – \(\frac{2}{5}\) + 8 + \(\frac{9}{10}\)
Solving the whole numbers
-12 + 8 = -4
– \(\frac{2}{5}\) + \(\frac{9}{10}\)
LCD of 5 and 10 is 10
– \(\frac{4}{10}\) + \(\frac{9}{10}\) = \(\frac{1}{2}\)
-4 + \(\frac{1}{2}\) = -3\(\frac{1}{2}\)

Question 18.
45.16 – 72.5 + (-63.72) + 50
__________________
Answer:
45.16 – 72.5 + (-63.72) + 50
45.16 + 50 -(72.5 + 63.72) = -41.60

Question 19.
-27 – 6.5 + (-1.3) + 28\(\frac{7}{10}\)
Answer:
-27 – 6.5 + (-1.3) + 28\(\frac{7}{10}\)
Convert from mixed fraction to the decimal numbers.
-27 – 6.5 + (-1.3) + 28.7
-27 – 6.5 – 1.3 + 28.7 = -6.1

Question 20.
-18 + 3.4 + (-2.5)
Answer:
-18 + 3.4 + (-2.5)
-18 – 2.5 + 3.4 = -17.1

Question 21.
–\(\frac{5}{6}\) + 1\(\frac{1}{3}\) – 3.3
Answer:
–\(\frac{5}{6}\) + 1\(\frac{1}{3}\) – 3.3
Convert from mixed fraction to the decimal numbers.
-0.8 + 1.3 – 3.3 = -2.8
Thus, –\(\frac{5}{6}\) + 1\(\frac{1}{3}\) – 3.3 = -2.8

Question 22.
–\(\frac{2}{5}\) – 4\(\frac{1}{10}\) + (-10.53)
Answer:
–\(\frac{2}{5}\) – 4\(\frac{1}{10}\) + (-10.53)
Convert from mixed fraction to the decimal numbers.
-0.4 – 4.1 + (-10.53) = -15.03
Thus –\(\frac{2}{5}\) – 4\(\frac{1}{10}\) + (-10.53) = -15.03

Question 23.
-2\(\frac{3}{5}\) – 3\(\frac{1}{2}\) + 1\(\frac{7}{10}\) + (-3\(\frac{3}{10}\))
Answer:
-2\(\frac{3}{5}\) – 3\(\frac{1}{2}\) + 1\(\frac{7}{10}\) + (-3\(\frac{3}{10}\))
-2\(\frac{3}{5}\) – 3\(\frac{1}{2}\) + 1\(\frac{7}{10}\) – 3\(\frac{3}{10}\)
Convert from mixed fraction to the decimal numbers.
2\(\frac{3}{5}\) = \(\frac{13}{5}\) = 2.6
3\(\frac{1}{2}\) = \(\frac{7}{2}\) = 3.5
1\(\frac{7}{10}\) = \(\frac{17}{10}\) = 1.7
3\(\frac{3}{10}\) = \(\frac{33}{10}\) = 3.3
-2.6 – 3.5 + 1.7 – 3.3 = -7.7
-2\(\frac{3}{5}\) – 3\(\frac{1}{2}\) + 1\(\frac{7}{10}\) + (-3\(\frac{3}{10}\)) = -7.7
7.7 can be written as 7\(\frac{7}{10}\)
-2\(\frac{3}{5}\) – 3\(\frac{1}{2}\) + 1\(\frac{7}{10}\) – 3\(\frac{3}{10}\) = -7\(\frac{7}{10}\)

Question 24.
-15.35 + 83.5 + (-16.98) + 1.8
Answer:
-15.35 + 83.5 + (-16.98) + 1.8
(-15.35) + 83.5 + (16.98) + 1.8 = 52.97

Question 25.
Kasey had $98.17 in her account. Her receipts from the day are shown. Write and evaluate an expression to determine the balance in her account.
Answer:

Answer:
Given,
Kasey had $98.17 in her account.
Taco meal bill = $8.69
Abar transportation = $11.50
Fun stop = $12.21
98 – 8.69 – 11.50 – 12.21
98 – (8.69 + 11.5 + 12.21) = 65.6
The balance in her account = $65.60

Question 26.
Lupita rewrote an expression as follows. -5.5 + 10.63 + (-3.7) = -5.5 + (-3.7) + 10.63 Did she use the Commutative or the Associative Property? What is the sum?
Answer:
-5.5 + 10.63 + (-3.7) = -5.5 + (-3.7) + 10.63
No she did not use any property.
-5.5 + (-3.7) + 10.63 = 1.43

Question 27.
Construct Arguments Terrance adds the lengths of fabric that he has left from a project. The lengths of fabric, in inches, are 15\(\frac{1}{6}\), 11\(\frac{1}{3}\), and 17\(\frac{1}{2}\). Terrance began with 100 inches. Write and evaluate an expression to determine how much fabric he used in all. How did you solve this problem?
Answer:
Terrance adds the lengths of fabric that he has left from a project. The lengths of fabric, in inches, are 15\(\frac{1}{6}\), 11\(\frac{1}{3}\), and 17\(\frac{1}{2}\).
15\(\frac{1}{6}\) + 11\(\frac{1}{3}\) + 17\(\frac{1}{2}\)
15\(\frac{1}{6}\) + (11\(\frac{1}{3}\) + 17\(\frac{1}{2}\))
15\(\frac{1}{6}\) + (11 + \(\frac{1}{3}\) + 17 + \(\frac{1}{2}\))
15\(\frac{1}{6}\) + (11 + 17 + \(\frac{1}{3}\) + \(\frac{1}{2}\))
15\(\frac{1}{6}\) + (28 + \(\frac{1}{3}\) + \(\frac{1}{2}\))
15\(\frac{1}{6}\) + (28 + \(\frac{5}{6}\))
15\(\frac{1}{6}\) + (28 \(\frac{5}{6}\))
15\(\frac{1}{6}\) + 28 \(\frac{5}{6}\)
15 + \(\frac{1}{6}\) + 28 + \(\frac{5}{6}\)
15 + 28 + \(\frac{1}{6}\) + \(\frac{5}{6}\)
15 + 28 + \(\frac{6}{6}\)
15 + 28 + 1 = 44
Terrance began with 100 inches.
100 – 44 = 56 inches

Question 28.
Overnight, the temperature increased by 3\(\frac{1}{2}\) °F. The temperature began at —7.9 °F. Write and evaluate an expression to determine the current temperature.
Answer:
Given,
Overnight, the temperature increased by 3\(\frac{1}{2}\) °F.
The temperature began at —7.9 °F.
3\(\frac{1}{2}\) – 7.9
3.5 – 7.9 = -4.4 °F.

For Problems 29-36, evaluate each expression.

Question 29.
(-5.8 + 9.1) – (-2\(\frac{1}{4}\))
Answer:
(-5.8 + 9.1) – (-2\(\frac{1}{4}\))
3.3 – (-2\(\frac{1}{4}\))
3.3 + 2\(\frac{1}{4}\)
Now convert the mixed fraction to decimal numbers.
2\(\frac{1}{4}\) = 2.25
3.3 + 2.25 = 5.55
Thus, (-5.8 + 9.1) – (-2\(\frac{1}{4}\)) = 5.55

Question 30.
(15\(\frac{1}{2}\) + 2.6) – 18\(\frac{3}{5}\)
Answer:
(15\(\frac{1}{2}\) + 2.6) – 18\(\frac{3}{5}\)
Now convert the mixed fraction to decimal numbers.
15\(\frac{1}{2}\) = 15.5
18\(\frac{3}{5}\) = \(\frac{93}{5}\) = 18.6
(15.5 + 2.6) – 18.6 = 18.1 – 18.6 = -0.5

Question 31.
10.2 – (-2.14 – 4.9)
Answer:
10.2 – (-2.14 – 4.9)
10.2 – (-(2.14 + 4.9))
10.2 – (-7.04)
10.2 + 7.04 = 17.24

Question 32.
-13\(\frac{3}{4}\) + 5\(\frac{1}{3}\)
Answer:
-13\(\frac{3}{4}\) + 5\(\frac{1}{3}\)
Rewriting the expression by separating the parts
-13 – \(\frac{3}{4}\) + 5 + \(\frac{1}{3}\)
Solving the whole number parts
-13 + 5 = -8
Solving the fraction parts
– \(\frac{3}{4}\) + \(\frac{1}{3}\)
LCD of 3 and 4 is 12
– \(\frac{9}{12}\) + \(\frac{4}{12}\) = –\(\frac{5}{12}\)
Now combine the whole and fraction parts
-8 – \(\frac{5}{12}\)  = -8\(\frac{5}{12}\)

Question 33.
-5.5 – (12.36 – 8.3)
Answer:
-5.5 – (12.36 – 8.3)
-5.5 – (4.06)
-5.5 – 4.06 = -9.56

Question 34.
(-4.25 – 8.7) + (-1\(\frac{1}{2}\)) – 2.5
Answer:
(-4.25 – 8.7) + (-1\(\frac{1}{2}\)) – 2.5
-12.95 – 1\(\frac{1}{2}\) – 2.5
Now convert the mixed fraction to decimal numbers.
-12.95 – 1.5 – 2.5
-(12.95 + 1.5 + 2.5) = -16.95
(-4.25 – 8.7) + (-1\(\frac{1}{2}\)) – 2.5 = -16.95

Question 35.
1\(\frac{9}{10}\) + (-4\(\frac{3}{4}\)) + (-7.93)
Answer:
1\(\frac{9}{10}\) + (-4\(\frac{3}{4}\)) + (-7.93)
Simplify the signs + × – = –
1\(\frac{9}{10}\) – 4\(\frac{3}{4}\) – 7.93
Now convert the mixed fraction to decimal numbers.
1\(\frac{9}{10}\) = \(\frac{19}{10}\) = 1.9
4\(\frac{3}{4}\) = \(\frac{19}{4}\) = 4.75
1.9 – 4.75 – 7.93 = -10.78
1\(\frac{9}{10}\) + (-4\(\frac{3}{4}\)) + (-7.93) = -10.78

Question 36.
-5\(\frac{2}{5}\) – 3.16 – (-1\(\frac{1}{8}\))
Answer:
-5\(\frac{2}{5}\) – 3.16 – (-1\(\frac{1}{8}\))
Simplify the signs
-5\(\frac{2}{5}\) – 3.16 + 1\(\frac{1}{8}\)
Now convert the mixed fraction to decimal numbers.
1\(\frac{1}{8}\) = \(\frac{9}{8}\) = 1.125
5\(\frac{2}{5}\) = \(\frac{27}{5}\) = 5.4
Now simplify the expressions
-5.4 – 3.16 + 1.125 = -7.435
Thus -5\(\frac{2}{5}\) – 3.16 – (-1\(\frac{1}{8}\)) = -7.435

Question 37.
Open Ended Write a word problem that includes using properties to add or subtract positive and negative numbers.
Answer:
At 4 pm the temperature in Australia was 28° C. By 2 am it had dropped by 16° C, but by 10 am the following morning it had risen by 11° C. What was the temperature in Australia now?

Lesson 4.4 More Practice/Homework

Apply Properties to Multi-step Addition and Subtraction Problems

Question 1.
Brian is adding the lengths of wood posts that he has left from building a pen for his chickens. The lengths are 3\(\frac{2}{3}\), 2\(\frac{1}{4}\), and 2\(\frac{1}{3}\) feet. Brian began with 20 feet of wood. Write and evaluate an expression to determine how much wood he used for the pen.

Answer:
Given,
Brian is adding the lengths of wood posts that he has left from building a pen for his chickens. The lengths are 3\(\frac{2}{3}\), 2\(\frac{1}{4}\), and 2\(\frac{1}{3}\) feet. Brian began with 20 feet of wood.
20 – 3\(\frac{2}{3}\) – 2\(\frac{1}{4}\) – 2\(\frac{1}{3}\)
\(\frac{240}{12}\) – \(\frac{44}{12}\) – \(\frac{27}{12}\) – \(\frac{28}{12}\)
\(\frac{141}{12}\) = 11\(\frac{3}{4}\) feet

Question 2.
At dinner time, the temperature outside was -13.9 °F. The temperature decreased by 12.8 °F overnight. Write and evaluate an expression to determine the temperature in the morning.
Answer:
Given,
At dinner time, the temperature outside was -13.9 °F.
The temperature decreased by 12.8 °F overnight.
Outside temperature = -13.9°F outside
Change in temperature = 13.9°F + 12.8 °F = 26.7 °F

Question 3.
Evaluate the expression. Identify the property used in each step.
\(\frac{3}{4}\) + (-\(\frac{3}{8}\)) + (-\(\frac{1}{4}\)) = –\(\frac{3}{8}\) + \(\frac{3}{4}\) + (-\(\frac{1}{4}\)) _______
= –\(\frac{3}{8}\) + [\(\frac{3}{4}\) + (-\(\frac{1}{4}\))] ________
= ____
Answer:
The property that is used in this expression is commutative property.
\(\frac{3}{4}\) + (-\(\frac{3}{8}\)) + (-\(\frac{1}{4}\))
= –\(\frac{3}{8}\) + \(\frac{3}{4}\) + (-\(\frac{1}{4}\))
= –\(\frac{3}{8}\) + [\(\frac{3}{4}\) + (-\(\frac{1}{4}\))]
= –\(\frac{3}{8}\) + [\(\frac{3}{4}\) –\(\frac{1}{4}\)]
= –\(\frac{3}{8}\) + \(\frac{1}{2}\)
LCD is 8 and 2 is 8.
= –\(\frac{3}{8}\) + \(\frac{4}{8}\)
= \(\frac{1}{8}\)

Question 4.
Open Ended Write a real-world problem that can be modeled by the equation 47\(\frac{1}{2}\) + (-47\(\frac{1}{2}\)) = o.
__________________
Answer:
47\(\frac{1}{2}\) + (-47\(\frac{1}{2}\)) = 0
+ × – = –
47\(\frac{1}{2}\) – 47\(\frac{1}{2}\) = 0

For Problems 5—14. evaluate each expression.

Question 5.
—12\(\frac{1}{2}\) – (-4.8)
Answer:
—12\(\frac{1}{2}\) – (-4.8)
—12\(\frac{1}{2}\) + 4.8
Convert from mixed fraction to the decimal form
-12.5 + 4.8 = -7.7
—12\(\frac{1}{2}\) – (-4.8) = -7.7

Question 6.
–\(\frac{9}{10}\) + (-18.6)
Answer:
–\(\frac{9}{10}\) + (-18.6)
-0.9 – 18.6
-(0.9 + 18.6)
-19.5
–\(\frac{9}{10}\) + (-18.6) = -19.5

Question 7.
89.2 + (-104.25) + (-17.9)
Answer:
89.2 + (-104.25) + (-17.9)
89.2 – 104.25 – 17.9
89.2 – (104.25 + 17.9)
89.2 – 112.15 = -22.95
89.2 + (-104.25) + (-17.9) = -22.95

Question 8.
9\(\frac{9}{10}\) + 9\(\frac{1}{8}\) – 12.85
Answer:
9\(\frac{9}{10}\) + 9\(\frac{1}{8}\) – 12.85
Convert from mixed fraction to the decimal form
9\(\frac{9}{10}\) = \(\frac{99}{10}\) = 9.9
9\(\frac{1}{8}\) = \(\frac{73}{8}\) = 9.125
(9.9 + 9.125) – 12.85
19.025 – 12.85 = 6.175
Thus 9\(\frac{9}{10}\) + 9\(\frac{1}{8}\) – 12.85 = 6.175

Question 9.
(-1.9 + (-2.5)) + 8.3
Answer:
(-1.9 + (-2.5)) + 8.3
– × + = –
-1.9 – 2.5 + 8.6
-(1.9 + 2.5) + 8.6
-4.4 + 8.6 = 4.2
Thus (-1.9 + (-2.5)) + 8.3 = 4.2

Question 10.
-10\(\frac{1}{2}\) – 19\(\frac{3}{4}\) – 15.2
Answer:
-10\(\frac{1}{2}\) – 19\(\frac{3}{4}\) – 15.2
-(10\(\frac{1}{2}\) + 19\(\frac{3}{4}\) + 15.2)
-(10.5 + 19.75 + 15.2) = -(45.45)
-10\(\frac{1}{2}\) – 19\(\frac{3}{4}\) – 15.2 = -45.45

Question 11.
(-2.8 + 4.98) + (-3.87)
Answer:
(-2.8 + 4.98) + (-3.87)
-2.8 – 4.98 – 3.87
-(2.8 + 4.98 + 3.87)
-11.65
(-2.8 + 4.98) + (-3.87) = -11.65

Question 12.
-24 + (-7\(\frac{3}{10}\)) + 4.3
Answer:
-24 + (-7\(\frac{3}{10}\)) + 4.3
-24 + 4.3 – 7\(\frac{3}{10}\)
-19.7 – 7\(\frac{3}{10}\)
= -19.7 – 7.3
= -27
Thus, -24 + (-7\(\frac{3}{10}\)) + 4.3 = -27

Question 13.
(-5.8 + 9.1) + (-2\(\frac{1}{4}\))
Answer:
(-5.8 + 9.1) + (-2\(\frac{1}{4}\))
3.3 + (-2\(\frac{1}{4}\)) = 3.3 + (-2.25)
3.3 – 2.25 = 1.05
Thus, (-5.8 + 9.1) + (-2\(\frac{1}{4}\))= 1.05

Question 14.
12\(\frac{3}{4}\) – 6\(\frac{1}{10}\) – (-8.4)
Answer:
12\(\frac{3}{4}\) – 6\(\frac{1}{10}\) – (-8.4)
12\(\frac{3}{4}\) – 6\(\frac{1}{10}\) + 8.4
Convert from mixed fraction to the decimal form.
12.75 – 6.1 + 8.4 = 15.05
Thus, 12\(\frac{3}{4}\) – 6\(\frac{1}{10}\) – (-8.4) = 15.05

Test Prep

Question 15.
While Jackie was in Hawaii, she would dive for shells. One afternoon she dove 7.8 feet. Her next two dives were each 2\(\frac{1}{8}\) feet deeper than the dive before it. What were the elevations relative to the sea level of her second and third dives?
Answer:
Given,
While Jackie was in Hawaii, she would dive for shells.
One afternoon she dove 7.8 feet. Her next two dives were each 2\(\frac{1}{8}\) feet deeper than the dive before it.
Depth for her second dive
d2 = -(7.8 + 2\(\frac{1}{8}\))
d2 = -(7.8 + \(\frac{17}{8}\))
d2 = -9.925 feet
Depth of her third dive
d3 = -(7.8 + 2 × 2\(\frac{1}{8}\))
d3 = 12.05 feet
Hence the depth of her second and third dives is -9.925 feet and -12.05 feet.

Question 16.
On Friday, Ms. Patel told her reading group that if they read a combined total of 20 hours or more over the weekend, she would let them have a free period on Monday. The numbers of hours the students spent reading are in the table below. Do the students get a free period on Monday? Explain.

__________________
__________________
Answer:
2 + 1 \(\frac{1}{6}\) + 4.125 + 0.75 + 3\(\frac{1}{2}\) + 1.75 + \(\frac{5}{8}\) + 2\(\frac{1}{2}\) + 1\(\frac{5}{6}\) + 2\(\frac{3}{8}\)
= 2 + \(\frac{7}{6}\) + \(\frac{33}{8}\) + \(\frac{3}{4}\) + \(\frac{7}{2}\) + \(\frac{7}{4}\) + \(\frac{5}{8}\) + \(\frac{5}{2}\) + \(\frac{11}{6}\) + \(\frac{19}{8}\)
= \(\frac{16}{8}\) + \(\frac{33}{8}\) + \(\frac{6}{8}\) + \(\frac{14}{8}\) + \(\frac{5}{8}\)+ \(\frac{19}{8}\) + \(\frac{7}{6}\) + \(\frac{21}{6}\) + \(\frac{15}{6}\) + \(\frac{11}{6}\)
= \(\frac{93}{8}\) + \(\frac{54}{6}\)
= 11\(\frac{5}{8}\) + 9
= 20\(\frac{5}{8}\)
20\(\frac{5}{8}\) > 20

Question 17.
This morning, the temperature was 13\(\frac{1}{2}\) °F. During the day, the temperature increased by 5.6 °F. At night, the temperature decreased by 23.8 °F. What was the temperature after it decreased?
A. 19.1 °F
B. 4.7 °F
C. -4.7 °F
D. -18.2 °F
Answer:
Given,
This morning, the temperature was 13\(\frac{1}{2}\) °F.
During the day, the temperature increased by 5.6 °F.
The temperature after the increase is
13\(\frac{1}{2}\) + 5.6
13.5 + 5.6 = 19.1 °F.
At night, the temperature decreased by 23.8 °F.
19.1 – 23.8 = – 4.7 °F.
Option C is the correct answer.

Question 18.
Evaluate the expression: -7\(\frac{7}{8}\) + 3.7 – (-15.9).
Answer:
-7\(\frac{7}{8}\) + 3.7 – (-15.9)
-7\(\frac{7}{8}\) + 3.7 +15.9
-7\(\frac{7}{8}\) + 19.6
7\(\frac{7}{8}\) can be written in the decimal form as 7.875
-7.875 + 19.6 = 11.725

Spiral Review

Question 19.
Overnight, the temperature decreased by 17\(\frac{1}{2}\) °F. If the temperature began at -3.6 °F, what is the current temperature?
Answer:
Given,
Overnight, the temperature decreased by 17\(\frac{1}{2}\) °F.
The temperature began at -3.6 °F.
-3.6°F – 17\(\frac{1}{2}\) °F = -21.1°F

Question 20.
Pauline gets a 2% commission on her sales at her job. She sells $23,500 worth of products in May. How much commission does Pauline earn in May?
Answer:
Given,
Pauline gets a 2% commission on her sales at her job.
She sells $23,500 worth of products in May.
Multiply the percentage of commission with the worth of products.
2% = 2/100
2/100 × 23500 = 235 × 2 = 470
Thus Paul earn $470 in May.