Into Math Grade 7 Module 4 Lesson 3 Answer Key Compute Sums and Differences of Rational Numbers

We included HMH Into Math Grade 7 Answer Key PDF Module 4 Lesson 3 Compute Sums and Differences of Rational Numbers to make students experts in learning maths.

HMH Into Math Grade 7 Module 4 Lesson 3 Answer Key Compute Sums and Differences of Rational Numbers

I Can identify and write expressions to represent rational number problems.

Spark Your Learning
Ryan wants to go camping. The list of all the locations he would like to visit is shown in the table with their corresponding elevations. What is the greatest difference between any two of the elevations? Explain.

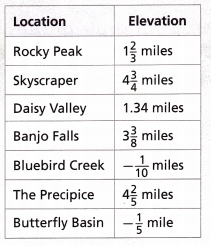
Turn and Talk Does it matter which way you subtract the values when finding distance? Why or why not?
Answer:
The greatest difference between Skyscraper and Daisy Valley is 4 3/4 – 1.34 miles
4.75 – 1.34 = 3.41 miles

Build Understanding

1. A scuba diver jumps in the water and continues to descend until reaching —10.75 feet. How far did the diver descend?

A. Use the number line to find the distance the diver traveled. Explain how you got your answer.

________________
________________
________________
________________

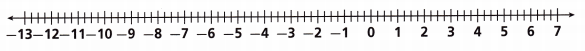
B. Write and evaluate a subtraction expression to find the distance the diver traveled starting from the diver’s elevation of 4.5 feet above sea level.
________________

C. Find the difference between the diver’s ending point and starting point.
________________

D. How are your answers to Parts B and C alike, and how are they different? Are they equal or opposites?
________________

E. Distance is always expressed as a positive number because it does not indicate direction. How can you use symbols to make sure that your result is always positive?
________________

Turn and Talk Do you think the Commutative Property is true for subtraction? Why or why not?

2. Evaluate -2.5 + 5 – (-4\(\frac{1}{4}\)).
A. Complete the number line to evaluate the expression.

The answer is ____
Answer:

-2.5 + 5 + 4\(\frac{1}{4}\)
2.5 + 4.25 = 6.75
B. Complete the rule to add the first two numbers of the expression.
_____ the absolute values and take the sign of the one with the
_____ absolute value.
Answer: The absolute value is 6.75 or 6\(\frac{3}{4}\)
C. Explain how the number line supports the rule used in Part B.
_______________________
_______________________
_______________________

D. Write the rule to subtract (-4\(\frac{1}{4}\)) from your answer to Part B. Show the work to use the rule to find the answer.
_______________________
_______________________

E. Explain how the number line supports the rule used in Part D.
_______________________
_______________________

F. In previous lessons, the rules were used with integers. Now they are being used with mixed numbers and decimals. Explain how the rules for adding and subtracting integers apply to rational numbers.
_______________________
_______________________

Turn and Talk Describe a context that could be modeled by the expression in Task 2.

Step It Out

3. A scientist is studying the effect temperature has on a specific bacteria. The table shows some of the data collected from the study.
A. The scientist reduces the temperature by 3.5 °C on Tuesday. What is the new temperature? Show your work.
_______________________

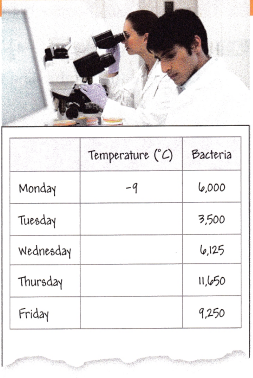
Answer:
Temperature on Monday = -9°C
Given that,
The scientist reduces the temperature by 3.5 °C on Tuesday.
-9 – 3.5 = -12.5 °C
New temperature on tuesday = -12.5 °C

B. On Wednesday, the temperature is increased by 20.7 °C. What is the new temperature? Show your work.
_______________________
Answer:

New temperature on tuesday = -12.5 °C
On Wednesday, the temperature is increased by 20.7 °C.
-12.5 + 20.7 = 8.2°C.
Thus new temperature on wednesday = 8.2°C.

C. Explain why your answer in Part B is reasonable.
_______________________
_______________________
_______________________
_______________________

D. On Thursday, the scientist increases the temperature by an additional 15.4 °C. What is the new temperature? Show your work.
_______________________
Answer:
temperature on wednesday = 8.2°C.
On Thursday, the scientist increases the temperature by an additional 15.4 °C.
15.4 + 8.2 = 23.6°C.
New temperature on thursday = 23.6°C.

E. On the final day of the study, the temperature is decreased by 5\(\frac{1}{2}\) °C. What is the new temperature? Show your work.
_______________________
Answer:
temperature on thursday = 23.6°C.
On the final day of the study, the temperature is decreased by 5\(\frac{1}{2}\) °C.
23.6 – 5.5 = 18.1°C.

Turn and Talk How would you explain to a friend why subtracting a negative number is the same as adding a positive number?

Check Understanding

Question 1.
An architect plans a courtyard with a width of 16.4 yards, then learns its width must change by -2.3 yards. What is the new width?
Answer:
Given,
An architect plans a courtyard with a width of 16.4 yards, then learns its width must change by -2.3 yards.
Let the old width be x
New width = old width + change in width
New width = x + (-2.3) = x – 2.3
16.4 = x – 2.3
16.4 + 2.3 = x
x = 18.7 yards

Question 2.
Evaluate -7\(\frac{1}{3}\) – (-\(\frac{2}{5}\)).
Answer:
-7\(\frac{1}{3}\) – (-\(\frac{2}{5}\)).
-7\(\frac{1}{3}\) + \(\frac{2}{5}\)
-7 – \(\frac{1}{3}\) + \(\frac{2}{5}\)
LCD of 3 and 5 is 15
– \(\frac{1}{3}\) + \(\frac{2}{5}\)
– \(\frac{5}{15}\) + \(\frac{6}{15}\) = \(\frac{1}{15}\)
-7 + \(\frac{1}{15}\) = -6\(\frac{14}{15}\)

On Your Own

Question 3.
Reason Ingvar is playing a video game that takes away points for losing treasures. His current score is shown, and then he loses a treasure worth 27.7 points.

A. Write and evaluate a subtraction expression to find Ingvar’s current score.
_________________________

Answer:
Ingvar’s current score = -56.2
He loses a treasure worth 27.7 points
-56.2 – 27.7 = -83.9

B. Is your answer reasonable? Why?
_________________________
Answer:
-56.2 + (-27.7)
-(56.2 + 27.7) = -83.9

Question 4.
In the stock market, changes in value used to be indicated by fractions, which represented portions of $1. If a stock had a value of $11.50, write and evaluate an addition expression to find how much the stock is worth after an increase of \(\frac{1}{4}\).
Answer:

Question 5.
Jayvon has 33.6 points in a competition. He loses 5.5 points. Write and evaluate an addition expression to determine Jayvon’s current points.
Answer:
Given,
Jayvon has 33.6 points in a competition. He loses 5.5 points.
33.6 – 5.5 = 28.1 points

Question 6.
Malik earns an average of 4\(\frac{1}{2}\) points on his daily quizzes. Near the end of the quarter, his average decreases by \(\frac{3}{4}\) point. Write and evaluate a subtraction expression to find his current quiz grade average.
Answer:
Given,
Malik earns an average of 4\(\frac{1}{2}\) points on his daily quizzes.
Near the end of the quarter, his average decreases by \(\frac{3}{4}\) point.
4\(\frac{1}{2}\) – \(\frac{3}{4}\)
4 + \(\frac{1}{2}\) – \(\frac{3}{4}\)
\(\frac{1}{2}\) – \(\frac{3}{4}\) = –\(\frac{1}{4}\)
4 – \(\frac{1}{4}\) = 3\(\frac{3}{4}\) or 3.75

Question 7.
Financial Literacy Miss Aliyah’s checking account balance is $15.50. She withdraws $5.37. Write and evaluate a subtraction expression to find the new balance.
Answer:
Given,
Miss Aliyah’s checking account balance is $15.50. She withdraws $5.37.
15.50 – 5.37 = 10.13
Thus the new balance of Miss Aliyah is $10.13

For Problems 8-11, evaluate the expression.

Question 8.
\(\frac{5}{8}\) + \(\frac{1}{4}\)
Answer:
\(\frac{5}{8}\) + \(\frac{1}{4}\)
LCD of 8 and 4 is 8.
\(\frac{5}{8}\) + \(\frac{1}{4}\) = \(\frac{5}{8}\) + \(\frac{2}{8}\) = \(\frac{7}{8}\)

Question 9.
18.7 – 12.3
Answer:
18.7 – 12.3 = 6.4

Question 10.
-1\(\frac{1}{2}\) – (-\(\frac{1}{8}\))
Answer:
-1\(\frac{1}{2}\) – (-\(\frac{1}{8}\))
-1\(\frac{1}{2}\) + \(\frac{1}{8}\)
-1 – \(\frac{1}{2}\) + \(\frac{1}{8}\)
– \(\frac{1}{2}\) + \(\frac{1}{8}\)
LCD of 2 and 8 is 8.
– \(\frac{1}{2}\) + \(\frac{1}{8}\) = – \(\frac{4}{8}\) + \(\frac{1}{8}\) = –\(\frac{3}{8}\)
-1 –\(\frac{3}{8}\) = -1\(\frac{3}{8}\)

Question 11.
-5.75 + (-3.28)
________________
Answer:
-5.75 + (-3.28)
-5.75 – 3.28
-(5.75 + 3.28) = -9.03
Thus, -5.75 + (-3.28) = -9.03

Question 12.
Reason The picture shows the approximate temperatures at which most seawater boils and freezes. How many degrees are there between the boiling point and freezing point?

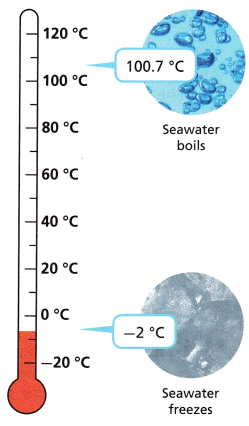
A. Will your answer be positive or negative? Explain.
_________________________
_________________________
_________________________
_________________________

B. Write and evaluate an expression to solve the problem. Write an expression to represent the problem. Use absolute value if appropriate based on Part A. Then solve the problem.
Answer:
Difference between the boiling point and freezing point.
100 – (-2) = 100 + 2 = 102 °C
So, the answer will be positive.

Question 13.
Brock rides a bike 22\(\frac{1}{8}\) miles to the nature preserve. On his way home, after 16\(\frac{1}{5}\) miles, he stops for lunch. How far is Brock from home? Write and evaluate an addition expression to solve the problem. Show your work.
Answer:
Given,
Brock rides a bike 22\(\frac{1}{8}\) miles to the nature preserve.
On his way home, after 16\(\frac{1}{5}\) miles, he stops for lunch.
22\(\frac{1}{8}\) + 16\(\frac{1}{5}\)
22 + \(\frac{1}{8}\) + 16 + \(\frac{1}{5}\)
Solving the whole number parts
22 + 16 = 38
Solving the fraction parts
\(\frac{1}{8}\) + \(\frac{1}{5}\)
LCD = 40
\(\frac{1}{8}\) + \(\frac{1}{5}\) = \(\frac{5}{40}\) + \(\frac{8}{40}\) = \(\frac{13}{40}\)

For Problems 14—19, evaluate the expression.

Question 14.
\(\frac{3}{8}\) + (-\(\frac{1}{2}\))
Answer:
\(\frac{3}{8}\) + (-\(\frac{1}{2}\))
+ × – = –
\(\frac{3}{8}\) – \(\frac{1}{2}\)
LCD of 8 and 2 is 8.
\(\frac{3}{8}\) – \(\frac{4}{8}\) = –\(\frac{1}{8}\)
Thus, \(\frac{3}{8}\) + (-\(\frac{1}{2}\)) = –\(\frac{1}{8}\)

Question 15.
16.34 – (-7.67)
Answer:
16.34 – (-7.67)
16.34 + 7.67 = 24.01

Question 16.
-9.36 + 4.48
Answer:
-9.36 + 4.48
-(9.36 – 4.48) = -(4.88)
-9.36 + 4.48 = -4.88

Question 17.
-2\(\frac{1}{2}\) – \(\frac{3}{4}\)
Answer:
-2\(\frac{1}{2}\) – \(\frac{3}{4}\)
Take ‘-‘ as common sign.
-(2\(\frac{1}{2}\) + \(\frac{3}{4}\))
-(2 + \(\frac{1}{2}\) + \(\frac{3}{4}\))
\(\frac{1}{2}\) + \(\frac{3}{4}\) = \(\frac{5}{4}\)
-(2 + \(\frac{5}{4}\))
-(2 + 1\(\frac{1}{4}\)) = – (2 + 1 + \(\frac{1}{4}\)) = -3\(\frac{1}{4}\)

Question 18.
\(\frac{5}{6}\) – \(\frac{1}{4}\)
Answer:
\(\frac{5}{6}\) – \(\frac{1}{4}\)
LCD of 6 and 4 is 12.
\(\frac{5}{6}\) – \(\frac{1}{4}\) = \(\frac{10}{12}\) – \(\frac{3}{12}\) = \(\frac{7}{12}\)
Thus, \(\frac{5}{6}\) – \(\frac{1}{4}\) = \(\frac{7}{12}\)

Question 19.
13.97 + 8.16
Answer:
13.97 + 8.16
13.97 + 8.16 = 22.13

I’m in a Learning Mindset!

How can I help others use a number line to depict subtraction?
Answer:
When we use a number line we jump backward for subtraction by counting logic.

Lesson 4.3 More Practice/Homework

Compute Sums and Differences of Rational Numbers

Question 1.
Mr. Leander bought two shirts for a total of $46.72. He returned one of the shirts for a refund of $24.61. Write and evaluate an addition expression to show what Mr. Leander paid for the shirt he kept.
Answer:
Given,
Mr. Leander bought two shirts for a total of $46.72.
He returned one of the shirts for a refund of $24.61.
(46.72 ÷ 2) – 24.61
23.36 – 24.61 = -1.25

Question 2.
STEM Scientists are studying the effects of increased temperature, which causes bleaching on coral reefs. A scientist dives at two different reefs, one located 34\(\frac{1}{2}\) feet below sea level and one at 26\(\frac{1}{4}\) feet below sea level. Write and evaluate a subtraction expression to find the change in elevation needed in order for the diver to reach the deeper reef. Explain why you have chosen a positive or negative sign for your answer.

Answer:
Given,
Scientists are studying the effects of increased temperature, which causes bleaching on coral reefs.
A scientist dives at two different reefs, one located 34\(\frac{1}{2}\) feet below sea level and one at 26\(\frac{1}{4}\) feet below sea level.
34\(\frac{1}{2}\) – 26\(\frac{1}{4}\)
(34 – 26) + (\(\frac{1}{2}\) – \(\frac{1}{4}\))
8 + \(\frac{1}{4}\)
8 \(\frac{1}{4}\) feet

Question 3.
Savana walks 3\(\frac{1}{3}\) miles to the local park. On her way home, she stops at Randolph’s house after 1\(\frac{2}{3}\) miles to pick up a book. Write and evaluate a subtraction expression to find how much farther Savana must walk to get home.

Answer:
Given,
Savana walks 3\(\frac{1}{3}\) miles to the local park.
On her way home, she stops at Randolph’s house after 1\(\frac{2}{3}\) miles to pick up a book.
3\(\frac{1}{3}\) – 1\(\frac{2}{3}\)
3 + \(\frac{1}{3}\) – 1 – \(\frac{2}{3}\)
Solving whole number parts
3 – 1 = 2
Solving fraction parts
\(\frac{1}{3}\) – \(\frac{2}{3}\) = –\(\frac{1}{3}\)
2 – \(\frac{1}{3}\) = (6 – 1)/3 = \(\frac{5}{3}\) = 1\(\frac{2}{3}\)
Thus Savana must walk 1\(\frac{2}{3}\) miles to get home.

Question 4.
Joseph removes \(\frac{5}{8}\) gallon of white paint from a can. Then he adds \(\frac{5}{8}\) gallon of blue paint to the can. Write and evaluate an addition expression to find the overall increase or decrease in the amount of paint in the can.
Answer:
Given,
Joseph removes \(\frac{5}{8}\) gallon of white paint from a can. Then he adds \(\frac{5}{8}\) gallon of blue paint to the can.
Removed white paint = \(\frac{5x}{8}\)
Added blue paint = \(\frac{5x}{8}\)
Total = x – \(\frac{5x}{8}\) + \(\frac{5x}{8}\) = x
Therefore there is no increase and decrease in the amount of paint in the can.

For Problems 5-8, evaluate the expression.

Question 5.
\(\frac{1}{4}\) – (-\(\frac{1}{6}\))
Answer:
\(\frac{1}{4}\) – (-\(\frac{1}{6}\))
\(\frac{1}{4}\) + \(\frac{1}{6}\)
LCD of 4 and 6 is 12.
\(\frac{1}{4}\) + \(\frac{1}{6}\) = \(\frac{3}{12}\) + \(\frac{2}{12}\) = \(\frac{5}{12}\)
So, \(\frac{1}{4}\) – (-\(\frac{1}{6}\)) = \(\frac{5}{12}\)

Question 6.
-233.2 – 25.8
Answer:
-233.2 – 25.8
Taking ‘-‘ as common
-(233.2 + 25.8) = -259

Question 7.
-4\(\frac{1}{2}\) + 2\(\frac{3}{4}\)
Answer:
-4\(\frac{1}{2}\) + 2\(\frac{3}{4}\)
-4.50 + 2.75 = -1.75
-4\(\frac{1}{2}\) + 2\(\frac{3}{4}\) = -1\(\frac{3}{4}\)

Question 8.
27.81 + (-13.97)
Answer:
27.81 + (-13.97)
27.81 – 13.97 = 13.84

Test Prep

Question 9.
Marianna had an average of 84.6 in social studies before her final exam. After the final exam, her average changed to 82.9.
A. Show how Marianna’s average changed in social studies.
__________________
__________________
Answer:
Marianna had an average of 84.6 in social studies before her final exam.
After the final exam, her average changed to 82.9.
82.9 – 84.6 = -1.7

B. Explain how you found your answer to Part A.
__________________
Answer:
If the initial average represents the 100%, then the percentage that the final average represents
(82.9/84.6) × 100% = 98%
So, we can say that her average decreased a 2% since the last exam.

Question 10.
A rock climber ascends 18\(\frac{3}{4}\) feet to the top of a rock ledge. The climber descends 8\(\frac{1}{8}\) feet and takes a break on a rock outcrop. Write and evaluate an addition expression to show how much farther the rock climber must descend to reach the original level.
Answer:
Given,
A rock climber ascends 18\(\frac{3}{4}\) feet to the top of a rock ledge.
The climber descends 8\(\frac{1}{8}\) feet and takes a break on a rock outcrop.
18\(\frac{3}{4}\) – 8\(\frac{1}{8}\)
18 + \(\frac{3}{4}\) – 8 – \(\frac{1}{8}\)
Convert from mixed fraction to the decimal form.
18.75 – 8.125 = 10.625

Question 11.
The total bill for a group’s restaurant order is $56.27. One meal was not prepared properly and came to the table late, so the manager credited the bill $18.46. What was the resulting bill for the group’s dinner?
Answer:
Given,
The total bill for a group’s restaurant order is $56.27.
One meal was not prepared properly and came to the table late, so the manager credited the bill $18.46.
56.27 – 18.46 = 37.81
Thus the resulting bill for the group’s dinner is $37.81

Question 12.
Keith buys 3 yards of material to make a blanket. He trims off a total of \(\frac{1}{6}\) yard before he begins sewing. How much material remains for the blanket?
A. \(\frac{1}{18}\)yard
B. \(\frac{2}{6}\) yard
C. 2\(\frac{5}{6}\) yards
D. 3\(\frac{1}{6}\) yards
Answer:
Given,
Keith buys 3 yards of material to make a blanket.
He trims off a total of \(\frac{1}{6}\) yard before he begins sewing.
3 – \(\frac{1}{6}\)
(6 × 3)/6 – 1/6
18/6 – 1/6 = (18 – 1)/6
17/6 = (12 + 5)/6
= \(\frac{12}{6}\) + \(\frac{5}{6}\)
= 2\(\frac{5}{6}\)
Thus option C is the correct answer.

Spiral Review

Question 13.
Gabe earns $10 per hour working for a landscaping business. He earned a raise to $10.75 per hour. What is the percent increase of Gabe’s wages? If necessary, round your answer to the nearest tenth of a percent.
Answer:
Given,
Gabe earns $10 per hour working for a landscaping business.
He earned a raise to $10.75 per hour.
The percent increase of Gabe’s wages:
($10.75 – $10)/$10 × 100%
0.75/10 × 100% = 7.5%
Thus the answer is 7.5%

Question 14.
The temperature at 5 p.m. was —4 °F. The temperature rose 7 °F once the sun came up at 8 a.m. the next morning. What was the temperature at 8 a.m. that morning?
Answer:
Given,
The temperature at 5 p.m. was —4 °F.
The temperature rose 7 °F once the sun came up at 8 a.m. the next morning.
-4 + 7 = 3°F
The temperature was 3°F at 8 a.m. that morning.