Into Math Grade 7 Module 15 Lesson 4 Answer Key Conduct Simulations

We included HMH Into Math Grade 7 Answer Key PDF Module 15 Lesson 4 Conduct Simulations to make students experts in learning maths.

HMH Into Math Grade 7 Module 15 Lesson 4 Answer Key Conduct Simulations

I Can use a simulation to test the probability of simple and compound events.

Step It Out

Question 1.
What is the experimental probability that you first find a winner on the second plate you check at the fundraiser dinner shown?

A. P(winning sticker) =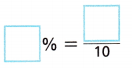
Answer:
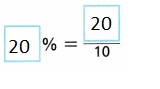= 2,

Explanation:
The experimental probability that I first find a winner on the second plate I check at the fundraiser dinner shown is 20% = 20/10 = 2.

B. Carlos uses whole numbers from 1 to 10 to design a simulation. He generates one number at random to simulate checking one plate.
Winning: 1, 2
Non-winning: 3, 4, 5, 6, 7, 8, 9, 10
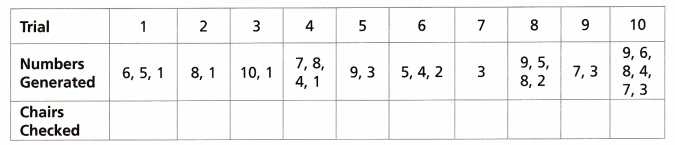
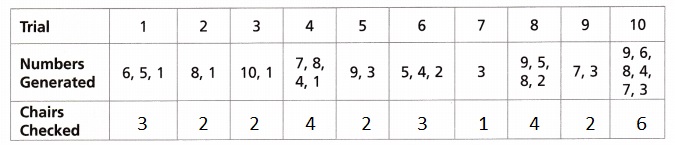
The table shows the results from Carlos’s experiment: generating numbers for each trial until a winning number (1 or 2) appears. Complete the table.

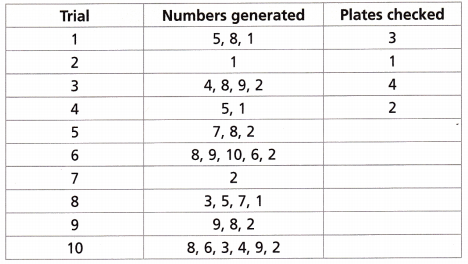
Answer:

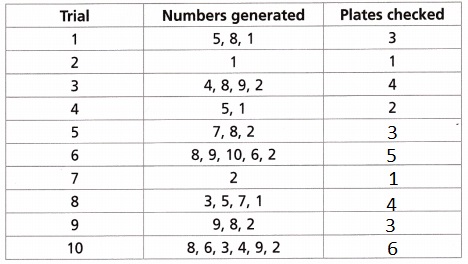
Explanation:
The table shows the results from Carlos’s experiment: generating numbers for each trial until a winning number (1 or 2) appears. Completed the table above.

C. For Trial 1, a winning number appeared after ___________ plate(s).
For Trial 2, a winning number appeared after _____________ plate(s).
How many of the 10 trials showed a winner on the second plate?
Answer:
For Trial 1, a winning number appeared after 3 plate(s), For Trial 2, a winning number appeared after 1 plate(s), 6 of the 10 trials showed a winner on the second plate,

Explanation:
If we see the table For Trial 1, a winning number appeared after 3 plate(s), For Trial 2, a winning number appeared after 1 plate(s) 6 of the 10 trials showed a winner on the second plate.

D. The experimental probability of first finding a winner on the second plate is , or ___________%.
Answer:
2 or 20%,

Explanation:
The experimental probability of first finding a winner on the second plate is 20/10 = 2 or 20%.

Question 2.
Manufacturers of Crunchy Flakes place a prize in 25% of their cereal boxes. Use a simulation to find the experimental probability that you will get at least one prize if you buy 3 boxes of Crunchy Flakes.
A. Design the experiment using whole numbers from 1 to 4.
Getting a prize: 1
Not getting a prize: _____________
Answer:
Not getting a prize is 2/3,

Explanation:
Given Manufacturers of Crunchy Flakes place a prize in 25% of their cereal boxes. Using a simulation to find the experimental probability that you will get at least one prize if you buy 3 boxes of Crunchy Flakes is 1/3 and not getting a prize is 2/3.

B. Label slips of paper with the whole numbers 1-4 and place them in a cup. Draw a number, record it, and place the number back in the cup. Use this process to generate 10 sets of 3 random whole numbers from 1 to 4. Record the results.
Answer:
1,3,4,2,3,1,2,4,2,1,

Explanation:
Labelled slips of paper with the whole numbers 1-4 and place them in a cup. Drawn a number, recorded it, and placed the number back in the cup. Using this process to generate 10 sets of 3 random whole numbers from 1 to 4. Recorded the results as 1,3,4,2,3,1,2,4,2,1.

C. The experimental probability is .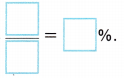
Answer:
25%,

Explanation:
The experimental probability is 1/4 = 1/4 X 100 = 25%.

Question 3.
The chance that Amir will make a free throw at any given time is shown. Find the experimental probability that Amir will make at least 3 of the next 5 free throws he attempts.

A. Choose a model to simulate this compound event.
Use whole numbers from 1 to 5. Amir makes free throws __________ % of the time. Let 1, 2, and 3 represent a successful free throw, and let and ___________ represent a missed free throw.
Answer:
Amir makes free throws 60% of the time, 4,5 represent a missed free throw,

Explanation:
Using whole numbers from 1 to 5. Amir made free throws 60% of the time. Let 1, 2, and 3 represent a successful free throw and let 4,5 represent a missed free throw.

B. Amir used a calculator to generate 10 trials of 5 random numbers from 1 to 5. Complete the table.

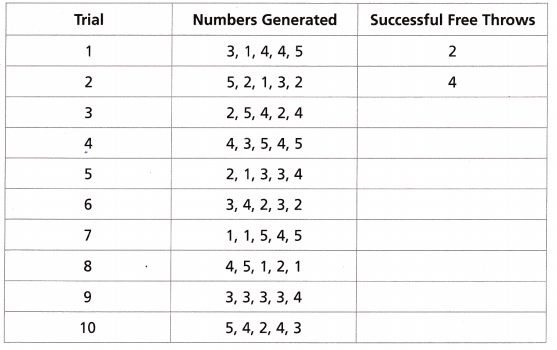
Answer:

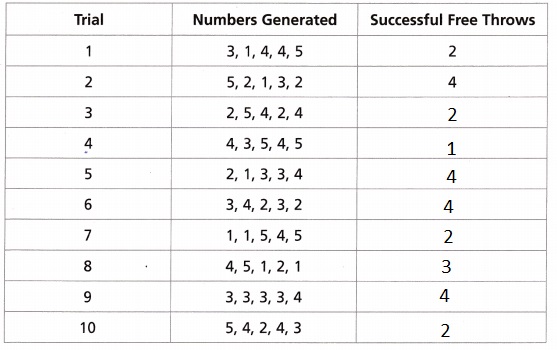
Explanation:
Amir used a calculator to generate 10 trials of 5 random numbers from 1 to 5. Completed the table as shown above.

C. List trials that represent at least 3 successful free throws.
Answer:
Trail 2, Trail 5, Trail 6, Trail 8 and Trail 9,

Explanation:
Using the table listed the trials that represent at least 3 successful free throws are Trail 2, Trail 5, Trail 6, Trail 8 and Trail 9.

D. Find the experimental probability that Amir makes at least 3 of the next 5 free throws he attempts.

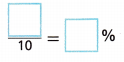
Answer:
6/10 = 60%,

Explanation:
The experimental probability that Amir makes at least 3 of the next 5 free throws he attempts is 6/10 = 60%.

Turn and Talk Explain how the model changes if the whole numbers from 1 to 10 were used to simulate this situation.
Answer:
Free throws will be 60% of the time,
1,2,3,4,5,6 represent a successful free throw and 7,8,9,10 represent a missed free throw,

Explanation:
If the model changes the whole numbers from 1 to 10 were used to simulate this situation then free throws will be 60% of the time, 1,2,3,4,5,6 represent a successful free throw and 7,8,9,10 represent a missed free throw.

Check Understanding

Suppose there is a 70% chance that Reagan will make a field goal at any given time. A computer was used to generate 10 sets of random numbers from 1 to 10, where the numbers 1-7 represent a successful field goal and numbers 8-10 represent a missed field goal. The results are shown.
Use the table for Problems 1-2.

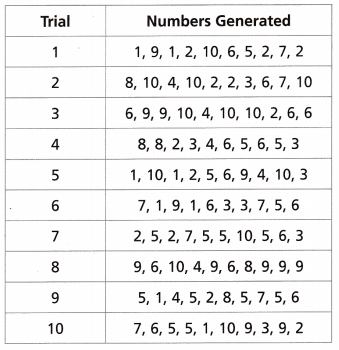
Question 1.
Find the experimental probability that Reagan will miss the first two field goals and make the third one.
Answer:
2/10 or 1/5,

Explanation:
The experimental probability that Reagan will miss the first two field goals and make the third one is 2 out of 10 so it is 2/10 or 1/5.

Question 2.
Each trial in the table shows a simulation of 10 field goal attempts. Which trials in the table show that Reagan made at least 7 of her field goal attempts? Use this information to find the experimental probability that Reagan will make at least 7 of the next 10 field goals attempted.
Answer:
Trail 5 and Trail 10, Probability is 70%,

Explanation:
Given each trial in the table showed a simulation of 10 field goal attempts. Trial 5 and trail 10 in the table showed that Reagan made at least 7 of her field goal attempts, Used this information to find the experimental probability that Reagan will make at least 7 of the next 10 field goals attempted is 7/10 X 100 = 70%.

On Your Own

Question 3.
Use Tools Lindsay randomly answers the questions on a 10-question true or false quiz. By guessing, she will get a question correct half the time. Explain how to model a simulation to find the experimental probability that Lindsay will answer at least 7 questions correctly.

Answer:
Lindsay answers 7 questions out of 10 correctly, So the probability is 7/10 or 70%
Explanation:
Given Lindsay randomly answers the questions on a 10-question true or false quiz. By guessing she will get a question correct half the time to model a simulation and to find the experimental probability that Lindsay will answer at least 7 questions correctly is Lindsay answers 7 questions out of 10 correctly so the probability is 7/10 or 70%

Question 4.
Use Structure At a new restaurant, 10% of the customers selected at random get a $5 coupon with their bill. Sasha wants to use a simulation to find the experimental probability that the second customer of the day gets a coupon with the bill. She uses a calculator to generate random numbers from 1 to 10. The number 1 represents a customer receiving a coupon and the numbers 2-10 represent a customer not receiving a coupon. The results of her simulation are shown in the table.

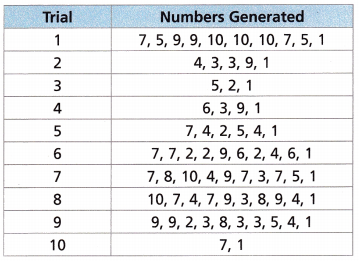
A. Which trials show the second customer getting a coupon? How many of the 10 trials show this event occuring?
Answer:
Trail 10, Only one trail,

Explanation:
Given at a new restaurant, 10% of the customers selected at random get a $5 coupon with their bill. Trail 10 shows the second customer getting a coupon. Out of 10 trails only one trail shows this event occuring.

B. Find the experimental probability that the second customer gets a coupon. Give your answer as a percent.
Answer:
1/10 or 10%,

Explanation:
The experimental probability that the second customer gets a coupon is only one so it is 1/10 or 1/10 X 100 = 10%.

C. Find the experimental probability that the tenth customer is the first one to receive a coupon. Give your answer as a percent.
Answer:
5/10 or 1/2 or 50%,

Explanation:
The experimental probability that the tenth customer is the first one to receive a coupon is 5 out of 10 is 5/10 or 1/2 in percent it is 1/2 X 100 = 50%.

Use the table and the information given for Problems 5 and 6.

Geography Over a 100-year period, the probability that a hurricane struck Reyna’s city in any given year was 20%. Reyna performed a simulation to find the experimental probability that a hurricane would strike the city in at least 4 of the next 10 years. In Reyna’s simulation, 1 represents a year with a hurricane.

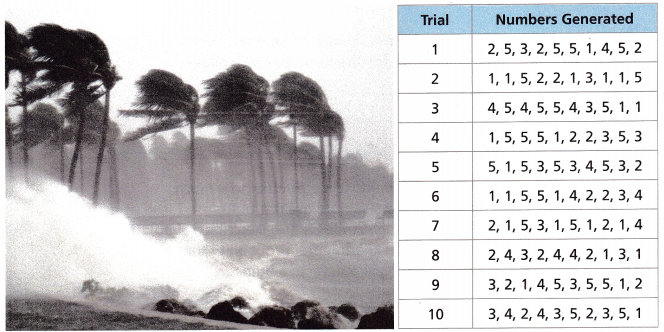
Question 5.
According to Reyna’s simulation, what was the experimental probability that a hurricane would strike the city in at least 4 of the next 10 years?
Answer:
4/10 or 2/5 or 40%,

Explanation:
According to Reyna’s simulation, the experimental probability that a hurricane would strike the city in at least 4 of the next 10 years is 4/10 or 2/5 or 40%.

Question 6.
Reason Suppose that over the 10 years following Reyna’s simulation, there was exactly 1 year in which a hurricane struck. How did this compare to the results of Reyna’s simulation?
Answer:
The probability for that year was very low compared to the results of Reyna’s simulation,

Explanation:
Suppose that over the 10 years following Reyna’s simulation, there was exactly 1 year in which a hurricane struck. Upon comparing to the results of Reyna’s simulation it is very low because the probability will be 1/10 or 10% which is very less to 40% of Reyna’s simulation.

Question 7.
Open-Ended Keith wants to use the spinner shown to simulate an event with a 75% chance of occurring. Describe a situation Keith could be simulating. Then describe how the spinner can be used.

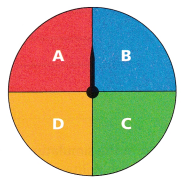
Answer:
Keith invited 5 friends to eat pizzas in a minute the maximum each can eat is 75%,
Keith simulated the eating of pizza through the spinner,

Explanation:
Keith wants to use the spinner shown to simulate an event with a 75% chance of occurring. A situation Keith could be simulating is Keith invited 5 friends to eat pizzas in a minute the maximum each can eat is 75%, Keith simulated the eating of pizza through the spinner each persons eats maximum of 75% means A, B, C on the spinner.

Question 8.
Use Tools Dave wants to generate random numbers to simulate an event with a 25% chance of occurring. Describe a model he could use.
Answer:
25%, 1 mean success and 2,3,4 will be unsuccessful,

Explanation:
As Dave wants to generate random numbers to simulate an event with a 25% chance of occurring. So to model he could use the number 1 for success out of 1 to 4 which is 25% and 2,3,4 will be unsuccessful.

Question 9.
Reason Is it possible to perform a simulation several times and get different experimental probabilities for the same event? Explain.
Answer:
Experimental probability is subject to change because the results of an experiment may change,

Explanation:
Experimental probability is determined by the actual results of an experiment. If a fair die is rolled 6 times and 3 is rolled out 2 out of the 6 times, the experimental probability of landing on the number 3 is 2/6 or 1/3 so experimental probability is subject to change because the results of an experiment may change.

Question 10.
STEM A quality control technician wants to determine how much variation can be expected in a random sample of light bulbs produced at a plant. The known rate of defective light bulbs is 5%. Describe a simulation the technician could use to find the experimental probability that a sample of 100 bulbs will include at least 5 defective bulbs.
Answer:
5/100, or 5%,

Explanation:
A simulation the technician could use to find the experimental probability that a sample of 100 bulbs will include at least 5 defective bulbs is 5/100 or 5%.

Question 11.
Allie is a softball player. She has a batting average of 0.600. This means that Allie gets a hit 60% of the time.
A. Design a simulation using slips of paper and a box to find the experimental probability of Allie getting a hit at least 2 out of 5 times.
Answer:
2/5 or 40%,

Explanation:
A simulation the technician could use to find the experimental probability that a sample of 100 bulbs will include at least 5 defective bulbs is 2/5 or 2/5 X 100 = 2 X 20 = 40%.

B. Use Tools Perform the simulation. Describe your results. Use the results to predict the probability of Allie getting a hit at least 2 out of 5 times.
Answer:
1,2 mean success hit and 3,4 and 5 will be unsuccessful hit,

Explanation:
The probability of Allie getting a hit at least 2 out of 5 times is 1,2 mean success hit and 3,4 and 5 will be unsuccessful hit.

Lesson 15.4 More Practice/Homework

Question 1.
There is a card under 30% of the chairs at a booster meeting. Finn wants to find the probability that the first card he finds will be under the third chair that he checks. He generates 10 sets of random numbers from 1 to 10. The numbers 1-3 represent a chair with a card and 4-10 represent a chair without a card. Complete the table, and find the experimental probability of the event.

Answer:

3/10 or 30%,

Explanation:
Given there is a card under 30% of the chairs at a booster meeting. Finn wants to find the probability that the first card he finds will be under the third chair that he checks. He generates 10 sets of random numbers from 1 to 10. The numbers 1-3 represent a chair with a card and 4-10 represent a chair without a card. Completed the table and found the experimental probability of the event as 3/10 or 30%.

Question 2.
Math on the Spot There is a 20% chance that a particular volcano will erupt during any given decade. A random number generator generated 10 sets of random numbers from 1 to 5 as shown. The number 1 represents the volcano erupting. Find the experimental probability that the volcano will erupt in 1 or 2 of the next 5 decades.

Answer:
The experimental probability is 2/10 or 20%,

Explanation:
Given there is a 20% chance that a particular volcano will erupt during any given decade. A random number generator generated 10 sets of random numbers from 1 to 5 as shown. The number 1 represents the volcano erupting. The experimental probability that the volcano will erupt in 1 or 2 of the next 5 decades is 2/10 or 20%.

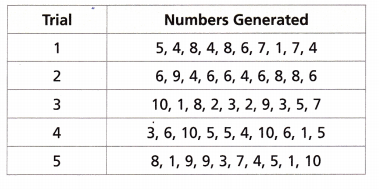
Question 3.
Sia makes 10% of the shots she attempts in soccer at any given time. A random number generator was used to generate 5 sets of random numbers from 1 to 10 as shown, where number 1 represents a successful shot and numbers 2-10 represent a missed shot. Find the experimental probability that Sia will make at least 2 of the next 10 shots attempted.

Answer:
The experimental probability is 2/10 or 20%,

Explanation:
Given Sia makes 10% of the shots she attempts in soccer at any given time. A random number generator was used to generate 5 sets of random numbers from 1 to 10 as shown, where number 1 represents a successful shot and numbers 2-10 represent a missed shot. The experimental probability that Sia will make at least 2 of the next 10 shots attempted is 2/10 or 2/10 X 100 = 20%.

Test Prep

Question 4.
There is a 25% chance that Jahil will hit an archery target on any given attempt. Which model can be used to find the experimental probability that Jahil will hit the target on at least 3 of the next 4 attempts?
(A) Use a computer to generate whole numbers from 1 to 8 where numbers 1-2 represent hitting the target and numbers 3-8 represent not hitting the target.
(B) Use a calculator to generate whole numbers from 1 to 8 where numbers 1-6 represent hitting the target and numbers 7-8 represent not hitting the target.
(C) Use a computer to generate whole numbers from 1 to 4 where numbers 1-2 represent hitting the target and numbers 3-4 represent not hitting the target.
(D) Use a calculator to generate whole numbers from 1 to 4 where numbers 1-3 represent hitting the target and number 4 represents not hitting the target.
Answer:
(D) Use a calculator to generate whole numbers from 1 to 4 where numbers 1-3 represent hitting the target and number 4 represents not hitting the target,

Explanation:
Given there is a 25% chance that Jahil will hit an archery target on any given attempt. The model can be used to find the experimental probability that Jahil will hit the target on at least 3 of the next 4 attempts as bit A and bit B has 8 numbers we require only 4 numbers,
in bit C we have 4 attempts but hitting target is 1-2 but we require at least 3 of the next 4 attempts so it is (D) Use a calculator to generate whole numbers from 1 to 4 where numbers 1-3 represent hitting the target and number 4 represents not hitting the target.

Question 5.
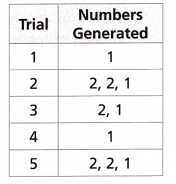
At a gym, 50% of the customers get a free training session. Let the number 1 represent a customer receiving a free training session and the number 2 represent not receiving a free training session. A calculator generated random numbers, 1 and 2, until a number that represents a customer receiving a free training session appeared. The results are shown in the table. Find the experimental probability that you must ask exactly 2 customers before you find a customer that received a free training session.

___________ %
Answer:
The experimental probability is 2/4 or 50%,

Explanation:
Given at a gym, 50% of the customers get a free training session. Let the number 1 represent a customer receiving a free training session and the number 2 represent not receiving a free training session. A calculator generated random numbers, 1 and 2, until a number that represents a customer receiving a free training session appeared. The results are shown in the table. The experimental probability that you must ask exactly 2 customers before we find a customer that received a free training session is 2/4 or 50%.

Question 6.
Out of 12 trials, a simulation showed Ming getting a place in a summer art program 10 times. What is the experimental probability of the event, according to the simulation?
Answer:
The experimental probability is 10/12 or 83.33%,

Explanation:
Given out of 12 trials, a simulation showed Ming getting a place in a summer art program 10 times. The experimental probability of the event, according to the simulation is 10/12 or 83.33%.

Spiral Review

Question 7.
Vera is going to flip a coin 50 times. Write and evaluate an expression to predict the number of times the coin lands on heads.
Answer:
50%,

Explanation:
There are two choices, heads and tails. We like one, heads. Tails is a no go.
So we count them. When we flip it once, we have one good option and one bad one. This happens every time. If there is a 50/50 chance for heads or tails, then on average half of the results will be favorable. 50 percent of the time(on average).

Question 8.
Juan spins two spinners each with 4 equal sections labeled 1-4. What is the probability that Juan spins a sum greater than 3?
Answer:
5/8,

Explanation:
If Juan spins two spinners each with 4 equal sections labeled 1-4. The probability that Juan spins a sum greater than 3 is  Event 1. 1 + 1 = 2, Event 2. 1 + 2 = 3,  Event 3. 2 + 1 = 3 these are less than 3 now other 5 it will be greater than 3 so it is 5/8.