We included HMH Into Math Grade 7 Answer Key PDF Module 14 Review to make students experts in learning maths.
HMH Into Math Grade 7 Module 14 Review Answer Key
Vocabulary
Complete each sentence using terms from the Vocabulary box.
Vocabulary
event
experiment
outcome
probability
sample space
trial
Question 1.
The _______________ of an experiment is the set of all possible outcomes of the experiment.
Answer: The sample space of an experiment is the set of all possible outcomes of the experiment.
Question 2.
The _____________ of an event is a number from 0 to 1, or from 0% to 100%, that describes its likelihood.
Answer: The probability of an event is a number from 0 to 1, or from 0% to 100%, that describes its likelihood.
Question 3.
Each repetition of a probability ___________ is called a ______________.
Answer: Each repetition of a probability experiment is called a trial.
Question 4.
Rolling a number less than 4 on a number cube is an ____________ that consists of more than one _____________.
Answer: Rolling a number less than 4 on a number cube is an event that consists of more than one outcome.
Concepts and Skills
Question 5.
The chance that a baseball player will get a hit is estimated to be 23%. How would you describe this likelihood?
(A) certain
(B) likely
(C) unlikely
(D) as likely as not
Answer:
23/100
It is unlikely.
Option C is the correct answer.
Question 6.
A news report states that a hurricane will reach land on Monday or Tuesday, but Tuesday is more likely. Give a number or number range to describe the probability that the hurricane will reach land on Tuesday.
Answer:
Given,
A news report states that a hurricane will reach land on Monday or Tuesday, but Tuesday is more likely.
Total = 2
The probability that the hurricane will reach land on Tuesday = 1/2 or 0.5
Question 7.
Indira drew 3 animals: an eagle, a snake, and a shark. She drew each animal twice, once with green eyes and once with red eyes. Ten students chose their favorite drawing. Three of them chose the shark with red eyes. How many possible outcomes are there in the sample space of her experiment? Based on the results, what is the experimental probability that a shark with red eyes is not picked, written as a percent?
Answer:
Given,
Indira drew 3 animals: an eagle, a snake, and a shark. She drew each animal twice, once with green eyes and once with red eyes.
Ten students chose their favorite drawing.
Three of them chose the shark with red eyes.
Out of 10, 3 choose the shark with red eyes.
Hence 7 did not choose them
P = 7/10 = 0.7 = 70%
Hence, there is a 70% experimental probability that a shark with red eyes is not picked.
For the total number of outcomes, there are 10 students, each with 3 choices 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 = 310
Question 8.
Use Tools Sophia randomly selects a marble from a bag of marbles and then replaces it. The results of 300 trials are shown. Based on this data set, what is the experimental probability of selecting a red marble from the bag? State what strategy and tool you will use to answer the question, explain your choice, and then find the answer.
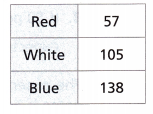
Answer:
Total number of marbles = 300
Number of red marbles = 57
Number of white marbles = 105
Number of blue marbles = 138
The experimental probability of selecting a red marble from the bag = P(R) = 57/300
Question 9.
In each cycle of a stoplight, the light is green for 30 seconds, yellow for 5 seconds, and red for 85 seconds. Liam conducts 500 trials of a simulation to estimate the likelihood that the stoplight will be a particular color when a car reaches it. Use the results to find the experimental probability of each event.

Answer:
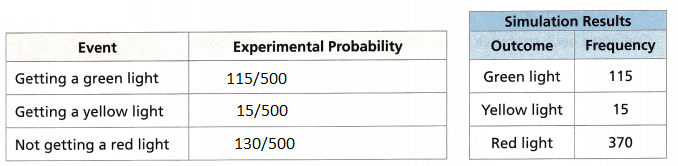
Total = 500
Green light outcome = 115
Yellow light outcome = 15
Red light outcome = 370
The experimental probability of getting a green light = 115/500
The experimental probability of getting a yellow light = 15/500
The experimental probability of not getting a red light = 115+15/500 = 130/500
Question 10.
A bag holds 6 plain bagels, 3 raisin bagels, 2 cheddar bagels, and 1 onion bagel. Grace chooses 4 bagels from the bag at random without replacing them. Select all possible compound events.
(A) All of the bagels are raisin bagels.
(B) There are exactly 2 plain bagels.
(C) More than half the bagels are cheddar bagels.
(D) There are more onion bagels selected than raisin bagels.
(E) The number of cheddar bagels is equal to the number of plain bagels.
Answer:
Given,
A bag holds 6 plain bagels, 3 raisin bagels, 2 cheddar bagels, and 1 onion bagel.
Grace chooses 4 bagels from the bag at random without replacing them.
A. 3 < 4
B. (3 + 2 + 1) > 2
6 > 2
C. 2 = 1/2 × 4
D. Onion 1 raisin can be 0.
E. 2 = 2, 1 = 1, 0 = 0
Options B, D, and E are possible events.
Question 11.
The experimental probability that Teresa will make a free-throw shot in basketball is 50%. Describe a simulation that can be used to estimate the probability that Teresa will make both of her next 2 free-throw shots.
Answer:
Question 12.
The table shows the blood types of the last 300 people to donate blood at a blood bank. Use this information to answer each question.
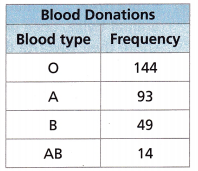
A. What is the experimental probability that the next person to donate blood will have type O blood?
Answer:
B. If 50 people donate blood on Friday, how many can be expected to have type O blood?
__________ people
Answer:
Question 13.
The experimental probability of winning a prize when playing a carnival game is estimated to be 4%. Based on this information, approximately how many times would a player need to play the game to win 10 prizes?
(A) 25 times
(B) 40 times
(C) 250 times
(D) 400 times
Answer:
Given,
The experimental probability of winning a prize when playing a carnival game is estimated to be 4%.
4/10 × 100 = 40 times
Option B is the correct answer.